02wk: 측도론 intro (2)

강의영상

https://youtube.com/playlist?list=PLQqh36zP38-zlQzcT1FJ8lBWRGkqBIsEu

강의노트 다운로드

!wget https://raw.githubusercontent.com/guebin/AP2023/main/posts/I.%20Measure%20Theory/2023-03-14-2wk.ipynb

--2023-03-14 18:55:02--  https://raw.githubusercontent.com/guebin/AP2023/main/posts/I.%20Measure%20Theory/2023-03-14-2wk.ipynb
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 185.199.110.133, 185.199.109.133, 185.199.111.133, ...
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|185.199.110.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 144568 (141K) [text/plain]
Saving to: ‘2023-03-14-2wk.ipynb.1’

2023-03-14-2wk.ipyn 100%[===================>] 141.18K  --.-KB/s    in 0.01s   

2023-03-14 18:55:02 (12.4 MB/s) - ‘2023-03-14-2wk.ipynb.1’ saved [144568/144568]

--2023-03-14 18:55:02--  http://2wk.ipynb/
Resolving 2wk.ipynb (2wk.ipynb)... failed: Name or service not known.
wget: unable to resolve host address ‘2wk.ipynb’
FINISHED --2023-03-14 18:55:02--
Total wall clock time: 0.05s
Downloaded: 1 files, 141K in 0.01s (12.4 MB/s)

예비개념1: 귀류법

- 귀류법: 니 논리 대로면… <- 인터넷 댓글에 많음..

님 논리대로면..
- XXX가 문제 없으면 서울 전체가 문제가 없고 (애초에 서울은 문제도 아니라는데 왜 이소리는 하고 계신지 모르겠지만)
- 수도권 모 대학이 문제가 없으면 전체가 문제가 없겠네요?
- 지방도 1개 대학이 문제가 없으니 전체가 문제 없겠네요?
와우! 모든 문제가 해결되었습니다! 출산율 감소로 인한 한국대학의 위기가 해결되었.. 아니 애초에 위기가 없었군요!.
어휴.. ㅠㅠ

ref: 하이브레인넷

예비개념2: 일반화

- 연필의 정의: 필기도구의 하나. 흑연과 점토의 혼합물을 구워 만든 가느다란 심을 속에 넣고, 겉은 나무로 둘러싸서 만든다. 1565년에 영국에서 처음으로 만들었다.

- 질문: 아래는 연필인가?

cardinality

• ref: https://en.wikipedia.org/wiki/Cardinality

- $A=\{2,4,6\}$ $\Rightarrow$ $|A|=3$, $A$ has a cardinality of 3.

- $A=\{1,2,3,4,\dots \}=\mathbb{N}$ $\Rightarrow$ $|A|=?$

• Cardinal number: 유한집합에서의 “갯수”라는 개념을 좀 더 일반화 하여 무한집합으로 적용하고 싶다.
• 유한집합: 우리가 친숙한 size 와 그 뜻이 같음
• 무한집합: 무한집합의 경우는 그 동작원리가 조금 더 복잡함

- 질문: $|\mathbb{Q}|<|{\mathbb{Q}}^c|$ ??

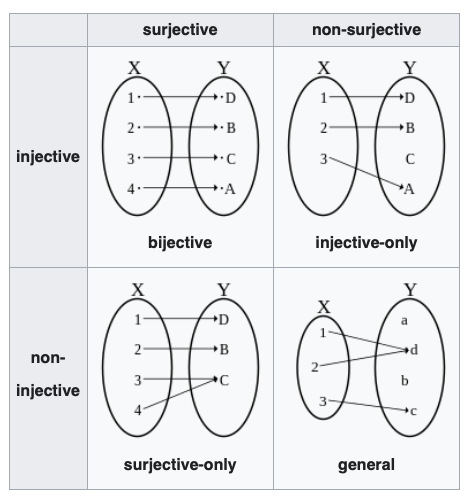
Bijection, injection and surjection (예비학습)

• ref: https://en.wikipedia.org/wiki/Bijection,_injection_and_surjection

- 용어 정리

• surjective = onto = 전사 = 위로의 함수
• injective = one-to-one = 단사 = 일대일 함수
• bijective = one-to-one and onto, one-to-one correspondence = 전단사 = 일대일 대응

- 따지는 방법:

• 단사: 함수 $f$는 $X$에서 $Y$로 향하는 단사함수이다. $\iff$ $\mathrm{\forall }{x}_1,x_2\in X$: $x_1\ne x_2\Rightarrow f(x_1)\ne f(x_2)$
• 전사: 함수 $f$는 $X$에서 $Y$로 향하는 전사함수이다. $\iff$ $\mathrm{\forall }y\in Y\mathrm{\exists }x\in X$ such that $f(x)=y$.

- 성질1: 어떤함수가 전사함수 & 단사함수 $\Rightarrow$ 전단사함수

- 성질2:

• 집합 $X$에서 집합 $Y$로 가는 단사함수 $f$가 존재한다. $\Rightarrow$ $|X|\le |Y|$
• 집합 $X$에서 집합 $Y$로 가는 전사함수 $f$가 존재한다. $\Rightarrow$ $|X|\ge |Y|$

(예비학습 끝)

- 성질1~2로 유추하면 아래와 같은 사실을 주장 할 수 있지 않을까?

• 집합 $X$에서 집합 $Y$로 향하는 전단사함수가 존재한다 $\Rightarrow$ $|X|=|Y|$

- 그렇다면 우리가 주장하고 싶은 것은 아래와 같이 된다.

• 유리수집합의 무리수집합의 cardinality는 다르다.
• 유리수집합과 무리수집합사이의 전단사함수는 존재할 수 없다.

유리수집합의 카디널리티

- 우리가 궁극적으로 궁금한 것

• 유리수집합과 무리수집합의 카디널리티는 다를까?

- 그냥 궁금한 것

• 자연수의 집합, 비음인 정수의 집합, 음의 정수의 집합, 정수의 집합, 짝수의 집합, 홀수의 집합의 카디널리티는 어떠할까?

- (예제1)

집합 $X=\{1,2,3\}$, $Y=\{2,4,6\}$을 생각하자. 적당한 함수 $f$를 아래와 같이 정의하자.

• $f(1)=2$
• $f(2)=4$
• $f(3)=6$

아래의 질문에 대답해보자.

1. (단사) 함수 $f$는 정의역의 모든 값에 대해 함수값이 모두 다른가? // $\mathrm{\forall }{x}_1,x_2\in X$, $x_1\ne x_2$ $\Rightarrow$ $f(x_1)\ne f(x_2)$?
2. (전사) 함수 $f$는 공역=치역인가? // $\mathrm{\forall }y\in Y\mathrm{\exists }x\in X$ such that $f(x)=y$.

1의 질문과 2의 질문이 모두 맞으므로 함수 $f$는 전단사 함수이다. 집합 $X$에서 집합 $Y$로 가는 전단사 함수가 존재하므로 집합 $X$와 집합 $Y$의 카디널리티는 동일하다.

- (예제2)

집합 $X=\{1,2,3,\dots \}$, $Y=\{2,4,6,\dots \}$을 생각하자. 적당한 함수 $f$를 아래와 같이 정의하자.

• $f(1)=2$
• $f(2)=4$
• $f(3)=6$
• $\dots$

아래의 질문에 대답해보자.

1. (단사) 함수 $f$는 정의역의 모든 값에 대해 함수값이 모두 다른가? // $\mathrm{\forall }{x}_1,x_2\in X$, $x_1\ne x_2$ $\Rightarrow$ $f(x_1)\ne f(x_2)$?
2. (전사) 함수 $f$는 공역=치역인가? // $\mathrm{\forall }y\in Y\mathrm{\exists }x\in X$ such that $f(x)=y$.

1의 질문과 2의 질문이 모두 맞으므로 함수 $f$는 전단사함수이다. 집합 $X$에서 집합 $Y$로 가는 전단사 함수가 존재하므로 집합 $X$와 집합 $Y$의 카디널리티는 동일하다.

- ${\mathrm{\aleph }}_0$ (알레프 널, 혹은 알레프 제로라고 읽음)

• 자연수집합 $\mathbb{N}$의 카디널리티는 ${\mathrm{\aleph }}_0$이다. 즉 $|\mathbb{N}|={\mathrm{\aleph }}_0$.
• 짝수인 자연수 집합의 카디널리티는 ${\mathrm{\aleph }}_0$이고, 홀수인 자연수 집합의 카디널리티는 ${\mathrm{\aleph }}_0$이다.
• 정수집합 $\mathbb{Z}$의 카디널리티는 ${\mathrm{\aleph }}_0$이다. 즉 $|\mathbb{Z}|={\mathrm{\aleph }}_0$.

- 느낌: ${\mathrm{\aleph }}_0$를 2배,3배,4배 하여도 ${\mathrm{\aleph }}_0$이다.

• 즉 무한집합의 경우, 본인과 카디널넘버가 같은 진 부분집합이 존재할 수 있다. (유한집합에서는 불가능하겠지)
• 무한집합의 정의: 집합 $A$가 무한집합이다. $\iff$ $A$와 동일한 카디널리티를 가지는 $A$의 진 부분집합이 존재한다.

- (예제3)

원소의 수가 $n$인 임의의 유한집합 $A$에 대하여 $|A|=n$ 이다.

- (예제4)

유리수집합의 카디널리티는 얼마인가? (https://en.wikipedia.org/wiki/Rational_number)

집합 $X$를 자연수의 집합이라고 하자. 집합 $Y$를 아래그림에 있는 숫자들의 집합이라고 하자.¹

¹ 그래서 일단 집합 $Y$는 양의 유리수의 집합을 포함한다

예를들어 집합 $X$와 집합 $Y$를 앞의 몇개만 써보면

• $X=\{1,2,3,4,5,6,\dots \}$
• $Y=\{1,\frac{2}{1},\frac{1}{2},\frac{3}{1},\frac{2}{2},\frac{1}{3},\dots \}$

함수 $f$를 아래와 같이 정의하자.

• $f(1)=1$
• $f(2)=2/1$
• $f(3)=1/2$
• $f(4)=3/1$
• $f(5)=2/2$
• $f(6)=1/3$
• $\dots$

함수 $f$는 $X$에서 $Y$로 향하는 전단사함수이다. $\Rightarrow$ $|X|={\mathrm{\aleph }}_0=|Y|$

(관찰) 임의의 양의 유리수의 집합 ${\mathbb{Q}}^{+}$는 모두 $Y$에 포함되어 있다. $\Rightarrow$ $X\subset {\mathbb{Q}}^{+}\subset Y$ $\Rightarrow$ $|{\mathbb{Q}}^{+}|={\mathrm{\aleph }}_0$

(생각) 그럼 음의 유리수의 집합 ${\mathbb{Q}}^{-}$의 카디널넘버 역시 ${\mathrm{\aleph }}_0$이다. 즉 $|{\mathbb{Q}}^{-}|={\mathrm{\aleph }}_0$.

(결론) 그럼 유리수의 카디널넘버는 ${\mathrm{\aleph }}_0$이다.² 좀 더 자극적으로 말하면 “자연수의 갯수와 유리수의 갯수는 같다” 라고 말할 수 있다.

² $\mathbb{Q}={\mathbb{Q}}^{+}\cup \{0\}\cup {\mathbb{Q}}^{-}$

- 조금 무식하게 쓰면 아래와 같이 쓸 수 있다.

• ${\mathrm{\aleph }}_0+1={\mathrm{\aleph }}_0$
• ${\mathrm{\aleph }}_0\times 2={\mathrm{\aleph }}_0$
• ${\mathrm{\aleph }}_0\times {\mathrm{\aleph }}_0={\mathrm{\aleph }}_0^2={\mathrm{\aleph }}_0$

실수집합의 카디널리티

- 아래의 관계가 성립했다.

• $|\mathbb{N}|={\mathrm{\aleph }}_0$
• $|\mathbb{N}\cup \{0\}|={\mathrm{\aleph }}_0$
• $|\mathbb{Z}|={\mathrm{\aleph }}_0$
• $|\mathbb{Q}|={\mathrm{\aleph }}_0$

- 그렇다면 아래는 어떠할까?

$$|\mathbb{R}|=??$$

(주장) 실수에 포함된 카디널넘버는 유리수의 카디널넘버 보다 크다.

• $\mathbb{Q}$에서 $\mathbb{R}$로 가는 단사함수는 존재하지만 전사함수는 존재할 수 없음을 보이면 된다.
• $\mathbb{N}$에서 $\mathbb{R}$로 가는 단사함수는 존재하지만 전사함수는 존재할 수 없음을 보여도 상관없다.³

³ $|\mathbb{Q}|=|\mathbb{N}|={\mathrm{\aleph }}_0$

(단사)

자연수에서 실수로 가는 단사함수는 존재한다. (자연수는 실수의 부분집합이니까)

(전사)

소망: $\mathbb{N}$에서 $\mathbb{R}$로 향하는 전사는 존재할 수 없음을 보이고 싶음.

소망2: 그런데 $\mathbb{N}$에서 $[0,1]$로 향하는 전사가 존재할 수 없음을 보여도 충분함.

전략: $\mathbb{N}$에서 $[0,1]$로 가는 전사가 존재한다고 가정하고 모순을 이끌어 내자.

1. 아래와 같은 주장을 하는 가상의 인물을 세움:

$\mathbb{N}$에서 $[0,1]$로 향하는 전사함수가 존재한다.

2. 그 가상의 인물이 하는 주장을 잘 생각해보면 아래와 같음

$f$는 정의역이 자연수이고 공역이 실수인 함수이므로 아래와 같은 형태일 것임.

• $f(1)=0.2344253456\cdots$
• $f(2)=0.3459837981\cdots$
• $f(3)=0.5452349871\cdots$
• $\dots$

그 가상의 인물의 주장대로라면

$$[0,1]=\{f(1),f(2),f(3),\dots \}$$

이라는 의미임.⁴

⁴ 다시 말하면 $[0,1]$ 사이의 모든 실수는 “셀수있다”라는 의미임

3. 전사함수의 정의에 의하여 아래가 성립해야 함

$\mathrm{\forall }y\in [0,1]\mathrm{\exists }x\in \mathbb{N}$ such that $f(x)=y$

아래의 원리에 따라서 $y=0.x_1{x}_2{x}_3\cdots$를 뽑는다면?

• $y$의 첫번째 소수점의 값 $x_1$은 $f(1)$의 첫번째 소수점과 다르게 한다. $\Rightarrow$ $y\ne f(1)$ $\Rightarrow$ $y\notin \{f(1)\}$
• $y$의 두번째 소수점의 값 $x_2$은 $f(2)$의 두번째 소수점과 다르게 한다. $\Rightarrow$ $y\ne f(1)$ and $y\ne f(2)$ $\Rightarrow$ $y\notin \{f(1),f(2)\}$

이러한 $y$는 분명히 실수이지만 $y\notin \{f(1),f(2),f(3),\dots ,\}$ 이다.⁵

⁵ 모순이네?

무리수집합의 카디널리티

(주장) 무리수집합의 카디널리티는 ${\mathrm{\aleph }}_0$가 아니다.

(쉐도복싱) 무리수집합의 카디널리티가 ${\mathrm{\aleph }}_0$ 이라고 하자.

• $\mathbb{R}=\mathbb{Q}\cup {\mathbb{Q}}^c$
• $|\mathbb{Q}|={\mathrm{\aleph }}_0$ 이므로 $\mathbb{Q}$와 $\mathbb{N}$사이에는 전단사함수가 존재함.
• $|{\mathbb{Q}}^c|={\mathrm{\aleph }}_0$ 이므로 ${\mathbb{Q}}^c$와 ${\mathbb{N}}^{-}=\{-1,-2,\dots \}$사이에는 전단사함수가 존재함.
• 따라서 $\mathbb{Q}\cup {\mathbb{Q}}^c$ 와 $\mathbb{N}\cup {\mathbb{N}}^{-}$ 사이에는 전단사함수가 존재함. (모순)