08wk: 측도론 (4)

Author

최규빈

Published

April 25, 2023

강의영상

youtube: https://youtube.com/playlist?list=PLQqh36zP38-xlxvNIex1h6j7lUQALgCU1

예비학습

$\cap_{n=1}^{\infty}(-\frac{1}{n},\frac{1}{n})=\{0\}$

- $\cap_{n=1}^{\infty}(-\frac{1}{n},\frac{1}{n}) =\{0\}$을 증명하라.

(증명)

step1: $\cap_{n=1}^{\infty}(-\frac{1}{n},\frac{1}{n})$은 원소로 $0$을 포함한다.

$\forall n \in \mathbb{N}$: $-\frac{1}{n} < 0 < \frac{1}{n}$

$\Leftrightarrow \forall n \in \mathbb{N}$: $0 \in (-\frac{1}{n},\frac{1}{n})$

$\Leftrightarrow$ $0 \in (-\frac{1}{1},\frac{1}{1})$ and $0 \in (-\frac{1}{2},\frac{1}{2})$ $\dots$

$\Leftrightarrow$ $0 \in (-\frac{1}{1},\frac{1}{1}) \cap (-\frac{1}{2},\frac{1}{2}) \cap \dots$

$\Leftrightarrow$ $0 \in \cap_{n=1}^{\infty}(-\frac{1}{1},\frac{1}{1})$

step2: $\cap_{n=1}^{\infty}(-\frac{1}{n},\frac{1}{n})$은 원소로 $0$보다 큰 임의의 양수를 포함하지 않는다.

포함한다고 가정하자. 즉

$\exists \delta >0$ such that $0+\delta \in \cap_{n=1}^{\infty}(-\frac{1}{n},\frac{1}{n})$

NOTE: From $\delta>0$, $\exists N \in \mathbb{N}$ such that $0<\frac{1}{N}<\delta$

THUS $\delta \notin (-\frac{1}{N},\frac{1}{N})$ $\Rightarrow$ CONTRADICTION! ($\because \cap_{n=1}^{\infty}(-\frac{1}{n},\frac{1}{n}) \subset (-\frac{1}{N},\frac{1}{N}))$

step3: $\cap_{n=1}^{\infty}(-\frac{1}{n},\frac{1}{n})$은 원소로 $0$보다 큰 임의의 음수를 포함하지 않는다.

Vacuous truth

- $P \Rightarrow Q$ 에서, $P$가 틀렸거나 $P$를 만족하는 집합이 공집합일 경우 $P\Rightarrow Q$라는 명제는 항상 참이되고 이러한 참을 배큐어스 트루 라고 말한다.

- 이해를 돕기 위한 예시

명제1: 최규빈교수보다 나이 많은 학생은 A+를 받지 못했다.
명제2: 최규빈교수보다 나이 많은 학생은 A+를 받았다.

여기에서 명제1,명제2는 모두 참이어야 한다. 그래야 명제1,명제2의 대우는 모두 참이 되며

대우1: A+를 받은 학생은 최규빈교수보다 나이가 적다.
대우2: A+를 받지 못한 학생은 최규빈교수보다 나이가 적다.

두 대우의 합성명제인 아래도 참이 된다.

A+을 받거나 받지 못한 학생은 최규빈교수보다 나이가 적다.

토폴로지

정의

- 정의: $\Omega$에 대한 부분집합의 모임 ${\cal T}$가 아래의 조건을 만족하면 ${\cal T}$를 $\Omega$의 토폴로지라고 부른다.

$\emptyset, \Omega \in {\cal T}$
$\forall A,B \in {\cal T}:~ A\cap B \in {\cal T}$ (finite intersection에 닫혀있음)
$\forall {\cal A} \subset {\cal T}: ~ (\cup_{A \in {\cal A}}A ) \in {\cal T}$ (uncoutable union, arbitrary union에 닫혀있음)

- $(\Omega,{\cal T})$를 위상공간 (topological space) 이라고 부른다. 그리고 ${\cal T}$의 원소를 ${\cal T}$-open set이라고 부른다.

- 모티브: 실수위에서의 열린구간 $(a,b)$의 개념을 추상화하고 싶음. 즉 open interval $\overset{일반화}{\to}$ open set 을 하고 싶음. 그리고 이러한 open set 만을 모은 collection ${\cal T}$라는 기호로 표현하고 싶음.

관찰1: $(1,3) \cap (2,4) = (2,3)$ // 2개의 open-interval을 교집합하니 open-interval이 나옴
관찰2: $\cap_{n=1}^{\infty}(1-\frac{1}{n},3+\frac{1}{n}) =[1,3]$ // countable many한 open-interval을 교집합하면 closed-interval이 나옴
관찰3: $\cup_{n=1}^{\infty}(1+\frac{1}{n},3-\frac{1}{n})= (1,3)$ // countable many한 open-interval을 합집합하면 open-interval이 나옴
관찰4: $\cup_{\epsilon>0}^{\infty}(1+\epsilon,3-\epsilon) =(1,3)$ // uncountalbe many한 open-interval을 합집합해도 open-interval이 나옴

- 왜 open interval을 추상화하고 싶을까?

open interval은 엄청 특이한 성질이 있음. 구간 $(a,b)$의 모든 점 $x$는 점 $x$를 포함하는 (아주 작은) 열린구간 $(x-\epsilon,x+\epsilon)$ 이 $(a,b)$사이에 존재함.
이 성질은 극한의 개념을 정의하기에 매우 유리하다. (따라서 연속, 끊어짐 등을 이해하기에도 좋다)

- $\Omega=\mathbb{R}$일 경우 open-set

$(1,2)$
$(1,2)\cup (5,6)$
$(a-\epsilon, a+\epsilon)$, where $\epsilon>0$ and $a\in\mathbb{R}$
$\dots$

- 체크

$\Omega=\mathbb{R}$, ${\cal T}=\{\emptyset, \Omega\}$라고 하자. ${\cal T}$는 $\Omega$에 대한 토폴로지이며 따라서 $(\Omega, {\cal T})$는 위상공간이 된다.
$\Omega=\mathbb{R}$, ${\cal T}=2^{\mathbb{R}}$라고 하자. 그렇다면 ${\cal T}$는 $\Omega$에 대한 토폴로지이며 따라서 $(\Omega,{\cal T})$는 위상공간이 된다.
그렇지만 우린 이런걸 쓰고 싶은게 아니야 ($\star$)

짧은지식

- 이론: $\Omega=\mathbb{R}$ 일때 ${\cal U}=\{O:O = \cup_{i=1}^{\infty}(a_i, b_i),~ a_i\leq b_i \in \mathbb{R}\}$라고 하자. 즉 ${\cal U}$는 open interval의 countable union으로 표현가능한 집합들의 모임이다. 그렇다면 $(\mathbb{R}, {\cal U})$는 위상공간이 된다.

그리고 특별히 이러한 위상 ${\cal U}$를 $\mathbb{R}$에서의 standard topology, Euclidean topology, 혹은 usual topology 라고 부른다. 사실 ${\cal U}$가 바로 우리가 토폴로지를 정의하는 이유이다 (매우 중요하다는 뜻이에요)

${\cal U}$의 원소를 원래 엄밀하게는 ${\cal U}$-open set이라고 불러야 하지만 이 경우는 ${\cal U}$를 생략하여 open set 이라고 부르기도 한다. 즉 우리가 일반적으로 말하는 “실수 $\mathbb{R}$에서의 열린집합, 혹은 그냥 열린집합” 은 ${\cal U}$-open set을 의미한다.

이 이론이 의미하는 바는 (1) 실수에서의 열린구간의 일반화 버전은 열린집합이며 (2) 열린집합은 열린구간의 가산합집합으로 표현가능하다 라는 뜻이다.

${\cal U}$를 한글로는 보통위상이라고 표현하기도 하지만 그렇게 널리 사용되지는 않는다. 하지만 따로 지칭할 용어가 마땅치 않아서 나는 그냥 보통위상이라고 부르겠다.

- 이론: $(\mathbb{R},{\cal U})$를 보통위상공간 (usual topological space) 이라고 하자. 모든 $O \in {\cal U}$ 는 아래를 만족한다.

$\forall o \in O, \exists a,b \in \mathbb{R}$ such that $o \in (a,b) \subset O \quad \cdots (\star)$

참고로 어떠한 집합 $O$에 대하여 $(\star)$를 만족하는 원소 $o$를 interior point of $O$ 라고 부른다. 따라서 어떤 집합의 모든 원소가 그 집합의 interior point라면 그 집합은 openset이라고 해석할 수 있다.

저는 나이테정리라고 외웠어요..

- 실수에서의 ${\cal U}$-openset 을 정의하는 방법

열린구간의 가산합집합
모든원소가 interior point인 집합

- 위상공간 $(\mathbb{R},{\cal U})$를 고려하자. 여기에서 ${\cal U}=\{O:O = \cup_{i=1}^{\infty}(a_i, b_i),~ a_i\leq b_i \in \mathbb{R}\}$를 의미한다. 아래의 사실들을 관찰하라.

모든 열린구간은 열린집합이다.
$(-\infty, a)$와 $(a,\infty)$는 모두 열린집합이다.
한점의 원소 $\{a\}$는 닫힌집합이다. ($\{a\}$의 여집합이 열린집합이므로)
$(-\infty, a]$와 $[a,\infty)$는 모두 닫힌집합이다.
공집합과 $\mathbb{R}$은 열린집합이다.¹ 따라서 공집합과 $\mathbb{R}$은 닫힌집합이다.

¹ 위상공간의 정의에따라 열린집합이라 주장할 수 있음. 혹은 $\mathbb{R}=\cup_{n=1}^{\infty}(-n,n)$이고 $\emptyset=(0,0)$이므로 열린집합이라 주장할 수 있음. 혹은 $\mathbb{R}$과 $\emptyset$의 모든 원소가 내점이므로 (공집합의 경우는 배큐어스트루에 의하여 모든 원소가 내점이다) 열린집합이라 주장할 수 있음

시그마필드 vs 토폴로지

	시그마필드	토폴로지
시작	“길이를 잴 수 있는 집합”이란 개념을 일반화 하고 싶다	“열린구간”의 개념을 일반화 하고 싶다
기호	${\cal F}$	${\cal T}$
공간	$(\Omega,{\cal F})$	$(\Omega,{\cal T})$
원소	${\cal F}$-measurable set, measurable set	${\cal T}$-open set
쓸모없는공간	$(\mathbb{R},2^{\mathbb R})$	$(\mathbb{R},2^{\mathbb R})$
쓸모있는공간	$(\mathbb{R},{\cal R})$	$(\mathbb{R},{\cal U})$

${\cal R}$이 뭔데..?

측도론의 유산

Borel $\sigma$-field

- 정의: $(\mathbb{R}, {\cal U})$를 보통위상공간이라고 하자. 아래와 같은 시그마필드를 Borel $\sigma$-algebera on $\mathbb{R}$이라고 한다.

\[{\cal B}(\mathbb{R}):=\sigma({\cal U})\]

그리고 ${\cal B}(\mathbb{R})$의 원소를 Borel measurable sets이라고 부른다.

- 참고: 교재에서는 ${\cal B}(\mathbb{R})$를 ${\cal R}$로 표현하기도 한다.

- 이론: 아래와 같은 집합을 고려하자.

${\cal A}_1:= \{A\subset \mathbb{R}: A \text{ is open}\}$²
${\cal A}_2:= \{(a,b): a,b \in \mathbb{R}, a<b\}$
${\cal A}_3:= \{[a,b): a,b \in \mathbb{R}, a<b\}$
${\cal A}_4:= \{(a,b]: a,b \in \mathbb{R}, a<b\}$
${\cal A}_5:= \{[a,b]: a,b \in \mathbb{R}, a<b\}$
${\cal A}_6:= \{(-\infty,b): a,b \in \mathbb{R}, a<b\}$
${\cal A}_7:= \{(-\infty,b]: a,b \in \mathbb{R}, a<b\}$
${\cal A}_8:= \{(a,\infty): a,b \in \mathbb{R}, a<b\}$
${\cal A}_9:= \{[a,\infty): a,b \in \mathbb{R}, a<b\}$

² 여기에서 open은 엄밀하게 말하면 usual topological spcace $(\mathbb{R},{\cal U})$ 에서의 ${\cal U}$-open set을 의미한다. 즉 보통위상공간에서 정의가능한 openset을 의미한다.

아래가 성립한다.

\[{\cal R}:={\cal B}(\mathbb{R}) = \sigma({\cal A}_1)=\sigma({\cal A}_2)=\dots=\sigma({\cal A}_9)\]

(증명??) – 증명까지는 아니고 그냥 설명..

예비학습1: countable union의 countable union은 countable union이다.

\[\mathbb{Q}^+ = \cup_{m \in \mathbb{N}}\big(\cup_{n \in \mathbb{N}}\{m/n\}\big)\]

예비학습2: “$\sigma({\cal A}_1)$의 모든원소는 ${\cal A}_1$의 원소를 재료로하여 만들수 있다” 라고 표현할 수 있으며, 여기에서 “만들 수 있다” 라는 의미는 ${\cal A}_1$의 원소에 가산합집합, 가산교집합, 여집합, 차집합등의 연산을 적용하여 $\sigma({\cal A})$의 원소를 만들 수 있다라는 의미이다.

예비학습3: 아래의 연산들은 모두 시그마필드에서 닫혀있다.

가산합집합의 가산합집합
가산합집합의 가산합집합의 가산합집합
여집합의 가산교집합의 가산합집합의 차집합
$\dots$

즉 시그마필드는 가산합집합과, 여집합에 닫혀있고 그들의 합성연산에 닫혀있다고 해석할 수 있다.

이제 아래가 성립한다고 가정해보자.

$\sigma({\cal A}_1)$의 모든 원소는 ${\cal A}_1$의 원소를 이용하여 만들 수 있다. 즉 ${\cal A}_1$의 모든원소에 가산합집합, 여집합, 혹은 그들의 합성연산을 적용하여 $\sigma({\cal A}_1)$의 모든 원소를 나타낼 수 있다.
${\cal A}_1$의 모든 원소는 ${\cal A}_2$의 원소를 이용하여 만들 수 있다. 즉 ${\cal A}_1$의 모든원소에 가산합집합, 여집합 혹은 그들의 합성연산을 적용하여 ${\cal A}_2$의 모든 원소를 나타낼 수 있다.

그렇다면 궁극적으로는 ${\cal A}_2$의 원소를 가산합집합, 여집합, 혹은 그들의 합성연산을 적용하여 $\sigma({\cal A}_1)$를 표현할 수 있다는 의미이고 이는 ${\cal R}=\sigma({\cal A}_1)=\sigma({\cal A}_2)$를 의미한다. ${\cal R}=\sigma({\cal A}_3)=\sigma({\cal A}_4)=\dots=\sigma({\cal A}_9)$ 역시 유사하게 따질 수 있다.

- 이론: 위의 이론의 ${\cal A}_2,\dots,{\cal A}_9$에서 $\mathbb{R}$ 대신에 $\mathbb{Q}$를 사용해도 성립한다.

- NOTE: ${\cal A}_1,\dots,{\cal A}_9$는 모두 파이시스템이다.

르벡메져

- Thm: $\Omega=\mathbb{R}$ 에 대하여 아래와 같은 collection ${\cal A}$를 고려하자.

\[{\cal A}=\{(a,b]: a,b\in \mathbb{R}, a<b\}\]

그리고 아래와 같은 함수 $\tilde{m}:{\cal A} \to [0,\infty]$을 고려하자.

\[\tilde{m}((a,b]) = b-a\]

이러한 함수 $\tilde{m}$은 $(\mathbb{R},{\cal R})$에서의 메져 $m:{\cal R} \to [0,\infty]$로 쉽게 업그레이드 가능하며 이 업그레이드 결과는 유일하다.

(증명)

카라테오도리의 확장정리에 의하여

${\cal A}$가 세미링임을 체크하고
$\tilde{m}:{\cal A}\to[0,\infty]$이 ${\cal A}$에서 (1) additive (2) $\sigma$-subadditive (3) $\sigma$-finite 을 만족한다는 사실을 체크하면 된다.

된다. $\tilde{m}$이 $\sigma$-subaddtive 성질을 가진다는 것을 보이는 것이 어려운데 이는 받아들이자.

- 정의: 위의 이론에 의하여 업그레이드 된 메져 $m$을 르벡메져라고 한다.

- 이론: $(\mathbb{R},{\cal R})$를 잴 수 있는 공간이라고 하고, $m$을 이 공간에서의 르벡메져라고 하자. 아래와 같은 집합들의 모임을 생각하자.

${\cal A}_1:= \{A\subset \mathbb{R}: A \text{ is open}\}$
${\cal A}_2:= \{(a,b): a,b \in \mathbb{R}, a<b\}$
${\cal A}_3:= \{[a,b): a,b \in \mathbb{R}, a<b\}$
${\cal A}_4:= \{(a,b]: a,b \in \mathbb{R}, a<b\}$
${\cal A}_5:= \{[a,b]: a,b \in \mathbb{R}, a<b\}$
${\cal A}_6:= \{(-\infty,b): a,b \in \mathbb{R}, a<b\}$
${\cal A}_7:= \{(-\infty,b]: a,b \in \mathbb{R}, a<b\}$
${\cal A}_8:= \{(a,\infty): a,b \in \mathbb{R}, a<b\}$
${\cal A}_9:= \{[a,\infty): a,b \in \mathbb{R}, a<b\}$

${\cal A}_1,{\cal A}_2,\dots, {\cal A}_9$에서의 르벡메져와 그 값이 일치하지만 ${\cal R} - {\cal A}_1, \dots, {\cal R}-{\cal A}_9$ 등에서는 일치하지 않는 새로운 메져 $m'$은 존재할 수 없다. 즉 르벡메져는 ${\cal A}_1,\dots,{\cal A}_9$에서의 값으로 유일하게 결정된다.

(설명)

르벡메져는 $\sigma$-finite한 메져이고, ${\cal A}_{1}\dots{\cal A}_{9}$는 모두 “7wk-파이시스템에서의 확장이론(메져버전)”에 소개된 이론의 조건 1,2를 만족하는 파이시스템이다. 따라서 르벡메져의 값은 ${\cal A}_1\dots,{\cal A}_9$에서의 값으로 유일하게 결정된다.

자잘한 내용 모음

생략때문에 헷갈려

- 어떠한 수학교재에서, 아무말 없이 open set 이라고만 하면 보통위상공간 (usual topological space) 으로부터 정의되는 open set을 의미한다. 즉 usual topological space $(\mathbb{R},{\cal U})$에서 ${\cal U}$의 원소를 의미한다.

- 어떠한 수학교재에서, 아무말 없이 measurable set 이라고 하면 르벡측도로 잴 수 있는 집합을 말한다. 즉 $(\mathbb{R}, {\cal R})$ 에서의 ${\cal R}$의 원소를 의미한다. 즉 일반적으로 정의하는 “잴 수 있는 집합”에서 “잴 수 있다”는 의미는 “르벡측도로 잴 수 있다”는 의미이다.³ 일반적인 $(\Omega, {\cal F})$에서 ${\cal F}$의 원소는 ${F}-measurable set 이라고 표현해야 옳다.

³ 혹은 우리의 용어로는 “확률을 잴 수 있는” 정도의 뜻으로 받아들일 수 있다.

- 하지만 때에 따라서는 ${\cal F}$의 원소를 그냥 measurable set이라고 부른다.

예시1

여기에서 measuralbe set은 앞에서 정의한 ${\cal F}$의 원소라는 의미이다.

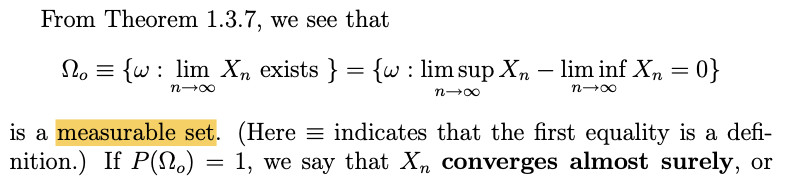
그림1: measurable set에 대한 교재의 언급, 눈치껏 그전의 문맥에서 정의한 ${\cal F}$-measurable set을 의미함을 알아들어야 함

- measure, measurable 등의 의미는 눈치껏 알아먹어야 한다.

예시2

일반적으로 measure라는 단어가 사용되면 “르벡측도로 재다”라는 의미를 지칭하는 경우가 많음

그림2: 여기에서 사용되는 “measure”의 의미는 문맥상 “르벡측도로 재다”라는 의미로 해석해야함

예시3

$(\Omega, {\cal F})$를 잴 수 있는 공간이라고 할 때는 meaure의 의미가 꼭 “르벡측도로 재다” 라는 것을 의미하는 건 아님

예시4

비탈리집합이 nonmeasurable set이라는 의미는 르벡측도로 측정불가능한 집합이라는 것을 의미함.

그림3: 여기에서 $N$은 비탈리집합을 의미하며 여기에서 “nonmeasurable” 이라는 뜻은 르벡메져로 측정불가능한 집합이라는 의미

토폴로지와 측도론의 논리전개

- 토폴로지와 측도론을 공부하면서 비슷한점이 있다고 느낌

- 비슷한점1: 모두 어떠한 속성을 가지는 집합을 “일반화” 하기 위해서 생겨났다. 예를들면, 잴 수 있는 집합이라는 것은 “수직선에서 길이를 잴 수 있는 집합”의 개념을 일반화하고 싶었어서 만들었으며, 열린집합이라는 것은 “수직선에서의 열린구간”이라는 개념을 일반화하고 싶어서 만들었다.

- 비슷한점2: 따라서 “잴 수 있는 집합들의 모임”, “열린집합들의 모임” 이라는 집합들의 집합이라는 장치를 고안하였다. 그리고 이러한 과정에서 일반적인 “길이(length)를 잴 수 있는 집합”의 속성, “열린구간”의 속성을 모아 “잴 수 있는 집합의 모임”, “열린집합의 모임” 을 정의하는 재료로 사용하였다.

- 비슷한점3: “잴 수 있는 집합들의 모임”, “열린집합들의 모임”의 원소를 각각 ${\cal F}$-mesurable set, ${\cal T}$-open set이라고 부르는 것도 유사하다.

- 비슷한점4: $\Omega=\mathbb{R}$에 대한 시그마필드와 토폴로지가 각각 ${\cal R}$이거나 ${\cal U}$이라면 그냥 잴 수 있는 집합, 열린 집합 이라고 부르는 것도 유사하다.

- 비슷한점5: 비슷한점4의 경우를 제외하고는 ${\cal F}$-mesurable set, ${\cal T}$-open set이라고 부르는게 원칙인데 이것도 문맥에 따라서 그냥 생략하고 쓰는 것도 유사하다. (사실 매번 언급하는게 귀찮기는 해)

- 비슷한점6: 일반화의 과정에서 발생하는 이상한 개념의 충돌이 존재한다.

잴 수 있는 집합의 모임을 $(\mathbb{R},2^\mathbb{R})$로 설정하면 비탈리집합도 잴 수 있다. (그렇지만 $(\mathbb{R}, {\cal R})$에서는 비탈리집합이 잴 수 없는 집합이므로 보통 책에서는 “잴 수 없는 집합”이라고 배운다)
열린집합의 모임을 $(\mathbb{R},2^\mathbb{R})$로 설정하면 한점만 포함하는 집합 $\{x\}$는 열린집합이 된다. (그렇지만 $(\mathbb{R},{\cal U})$에서는 한점만 포함하는 집합은 닫힌집합이므로 보통 책에서는 “한점만 포함하는 집합은 닫힌집합이다” 라고 배운다.

제 생각: 사실 이는 일반화 과정이 겪는 불가피한 문제인듯 해요. “문자, 그림, 기호 따위를 쓸 수 있는 도구” 정도로 펜슬의 의미를 확장하면 손가락도 펜슬이 되고, 발가락도 펜슬이 됩니다.

- 비슷한점7: 열린집합과 토폴로지, 잴수있는 집합과 시그마필드를 정의하는 두가지 루트가 존재한다.

루트1: 토폴로지를 먼저 정의하고 토폴로지의 원소가 열린집합이라고 정의한다. 혹은 시그마필드를 먼저 정의하고 시그마필드의 원소가 잴 수 있는 집합이라고 정의한다.
루트2: 열린집합을 정의하고 (집합의 모든 원소가 interior point이면 열린집합), 열린집합의 모임으로 토폴로지를 정의한다. 혹은 잴 수 있는 집합을 정의하고, 잴 수 있는 집합의 모임으로 시그마필드를 정의한다.