13wk-2: MCMC (1)

최규빈

2023-05-30

강의영상

youtube: https://youtube.com/playlist?list=PLQqh36zP38-zyk8psVKy2OaZs3zV4ExWn

import

import numpy as np
import matplotlib.pyplot as plt
import scipy

정리 (low-resolution)

- 우리가 하고 싶었던 것: 어떠한 현상에 대하여, 확률공간 $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ 에 대한 완전한 기술

- 이것을 수행하는 방법.

• 방법1: $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$를 state 하고 “관심있는 어떤 것”을 이론적으로 구한다.
• 방법2: $\omega \to \mathit{X}(\omega )=\mathit{x}$ 를 무한번 반복 관찰하고 (=시뮬레이션하고!) “관심있는 어떤 것”을 시뮬레이션으로 근사
• 방법3: 독립적으로 $n$회 관찰된 $({\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_n)$ 를 이용하여 “관심있는 어떤 것”을 추정, 추정 결과를 합리적으로 설득.

- 시뮬레이션 가능하면 최고인것 같은데?

- 통계학과 최고의 발명품

1. EM 알고리즘
2. FDR
3. 부스트랩

전통적인 난수생성 방법

균등분포

- 가정: 균등분포에서는 뽑을 수 있다고 가정한다. (제가 사실 여기는 잘 몰라요)

그림1: 균등분포를 생성하는 원리에 대하여 chatGPT에게 물어봄

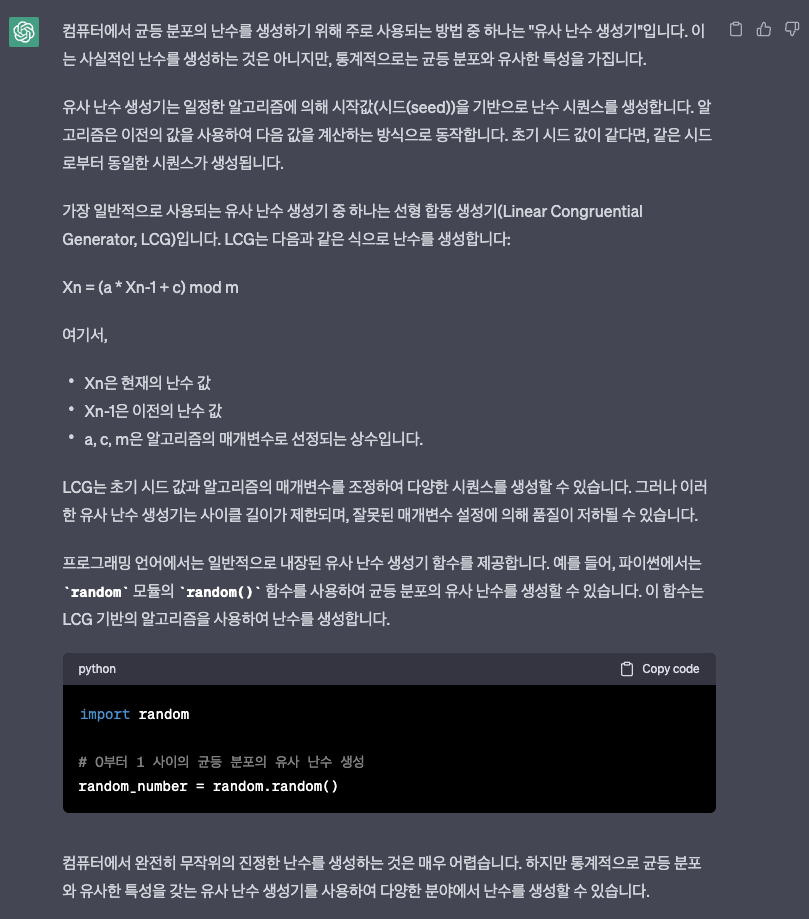
- 균등분포 이외의 난수는 어떻게?… (어려워요)

베르누이, 이항분포, 포아송, 지수분포

- 베르누이

x = np.random.rand(1000)
plt.hist(x);

fig, ax = plt.subplots(1,2)
ax[0].hist((x > 0.5)*1.0,color='C0');
ax[1].hist(np.random.binomial(1,0.5,size=1000),color='C1');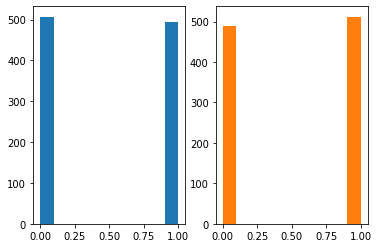

• $X\sim Ber(p)$, $p=0.5$

- 이항분포: 베르누이의 합으로!

x = np.random.rand(10*100000).reshape(10,100000)
fig, ax = plt.subplots(1,2)
ax[0].hist((x>0.5).sum(axis=0),bins=9);
ax[1].hist(np.random.binomial(10,0.5,size=100000),color='C1',bins=9);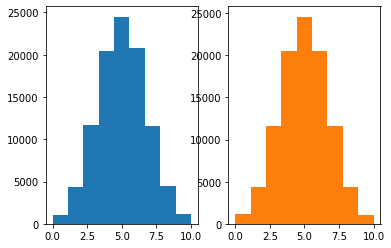

- 포아송: 이항분포의 근사로

• ref: https://guebin.github.io/SC2022/0324.html

- 지수분포: 포아송 프로세스를 이용하여!

• ref: https://guebin.github.io/SC2022/0324.html

inverse cdf, 박스뮬러변환

- inverse cdf: 지수분포를 뽑는 또 다른 테크닉: (지수분포가 아니더라도 CDF를 알면 뽑을 수 있음)

• ref: https://guebin.github.io/SC2022/0329.html

- 박스뮬러변환: 지수분포 + uniform으로 정규분포를 뽑는 테크닉

• ref: https://guebin.github.io/SC2022/0329.html

- 카이제곱분포, 감마분포: 지수분포를 이용하면 샘플링가능

• ref: https://guebin.github.io/SC2022/0419.html

베타분포를 샘플링 (전통적 방법)

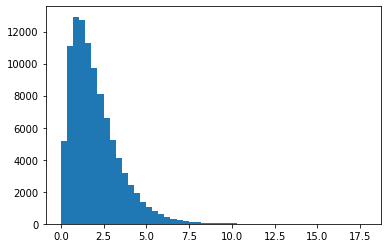
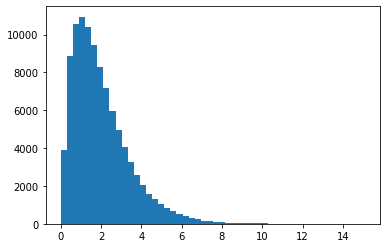
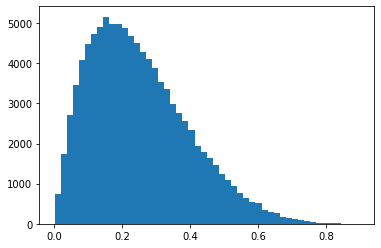
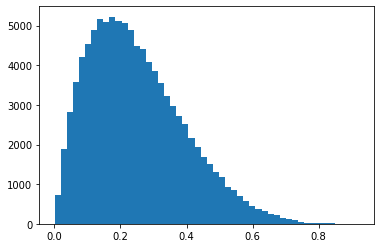
- 목표: $X_1,X_2,X_3,\dots ,X_{100000}\stackrel{i.i.d.}{\sim }\mathcal{B}(2,6)$

- 전략: 아래를 이용한다.

1. $\mathcal{B}(2,6)\stackrel{d}{=}\frac{\mathcal{G}(2,1)}{\mathcal{G}(2,1)+\mathcal{G}(6,1)}$
2. $\mathcal{G}(2,1)\stackrel{d}{=}\mathcal{E}(1)+\mathcal{E}(1)$
3. $\mathcal{G}(6,1)\stackrel{d}{=}\mathcal{E}(1)+\mathcal{E}(1)+\mathcal{E}(1)+\mathcal{E}(1)+\mathcal{E}(1)+\mathcal{E}(1)$

- inverse cdf를 이용하여 지수분포를 뽑을 수 있다고 가정하자.

gamma2 = np.random.exponential(scale=1,size=(100000,2)).sum(axis=1)
plt.hist(gamma2,bins=50);

plt.hist(np.random.gamma(shape=2,scale=1,size=100000),bins=50);

gamma6 = np.random.exponential(scale=1,size=(100000,6)).sum(axis=1)

beta26 = gamma2/(gamma2+gamma6)

plt.hist(beta26,bins=50);

plt.hist(np.random.beta(2,6,size=100000),bins=50);

베타분포를 샘플링 (이상한 방식)

pdf 정의

- 모티브: 그냥 pdf를 입력하면 알아서 샘플링되도록 할 수 없나?

- 예비학습: 감마함수

scipy.special.gamma(5)

24.0

g = scipy.special.gamma

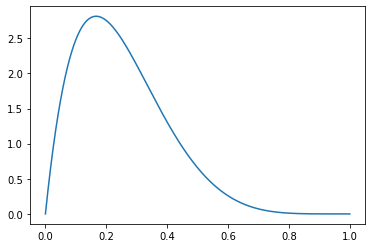
- 베타분포의 pdf

$$f_X(x)=\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{x}^{\alpha -1}(1-x{)}^{\beta -1}$$

def f(x): 
    return g(2+6)/(g(2)*g(6)) * x**(2-1) * (1-x)**(6-1)

_x = np.linspace(0,1,10000)
plt.plot(_x,f(_x))

시도1: 망했음

step1: 초기화

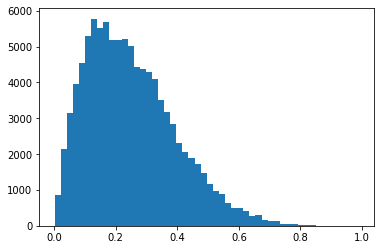
- 베타분포에서 10만개의 샘플을 뽑아보자.

- 일단 $\mathbf{x}\mathbf{x}=(x_0,x_1,\dots ,x_{T-1})$를 초기화를 하자.

xx=[0.99]
xx

[0.99]

• 현재의 $x_i$값은 $x_0=0.99$ 만 있지만 궁극적으로는 $\mathcal{B}(2,6)$에서 생성된 샘플로 채우고 싶다.

step2: 후보 샘플링

- 하나의 $y$ 을 균등분포에서 샘플링한다.

np.random.seed(1)
y = np.random.rand()
y

0.417022004702574

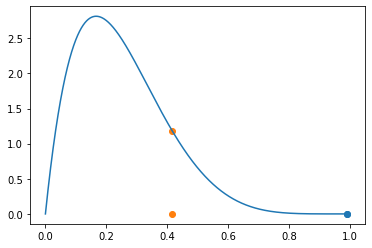
step3: 비교

- $xx[0]$ vs $y$

plt.plot(_x,f(_x))
plt.scatter(xx[0],0,color='C0')
plt.scatter(xx[0],f(xx[0]),color='C0')
plt.scatter(y,0,color='C1')
plt.scatter(y,f(y),color='C1')

<matplotlib.collections.PathCollection at 0x7ff3eca2eb50>

step4: 선택

- 비교결과: $xx[0]$ 보다 $y$가 나은것 같다

- 선택: $xx[1]=y$ 로 하자

만약에 $xx[0]$이 $y$보다 나은것 같다면? 그냥 $xx[1]=xx[0]$으로 선택

step 1~4 반복: 망했음

T = 100000
xx = [0.99]
for t in range(T):
    y = np.random.rand()
    if f(xx[t]) < f(y):
        xx.append(y) 
    else:
        xx.append(xx[t])

plt.hist(xx,bins=50);

시도2: 성공

step1: 초기화

- 베타분포에서 10만개의 샘플을 뽑아보자.

- 일단 $\mathbf{x}\mathbf{x}=(x_0,x_1,\dots ,x_{T-1})$를 초기화를 하자.

xx=[0.99]
xx

[0.99]

• 현재의 $x_i$값은 $x_0=0.99$ 만 있지만 궁극적으로는 $\mathcal{B}(2,6)$에서 생성된 샘플로 채우고 싶다.

step2: 후보 샘플링

- 하나의 $y$ 을 균등분포에서 샘플링한다.

np.random.seed(1)
y = np.random.rand()
y

0.417022004702574

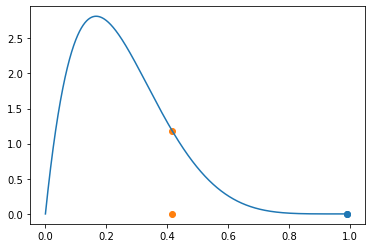
step3: 비교

- $xx[0]$ vs $y$

plt.plot(_x,f(_x))
plt.scatter(xx[0],0,color='C0')
plt.scatter(xx[0],f(xx[0]),color='C0')
plt.scatter(y,0,color='C1')
plt.scatter(y,f(y),color='C1')

<matplotlib.collections.PathCollection at 0x7ff85ef61b20>

step4: 선택

- 비교결과: $xx[0]$ 보다 $y$가 나은것 같다

- 선택: 그렇지만 무조건 $xx[1]=y$ 로 선택하면 큰일나겠음.. 아래의 확률로 선택하자!

• 확률 $\frac{f(xx[0])}{f(xx[0])+f(y)}$ 로 $xx[1]=xx[0]$을 선택!
• 확률 $\frac{f(y)}{f(xx[0])+f(y)}$ 로 $y$를 선택!

step 1~4 반복: 이게 된다고?

T = 100000
xx = [0.99]
for t in range(T):
    y = np.random.rand()
    thresh_prob = f(y)/(f(xx[t])+f(y)) ## thresh_prob 가 클수록 y가 선택
    _u = np.random.rand()
    if _u < thresh_prob:
        xx.append(y) 
    else:
        xx.append(xx[t])

plt.hist(xx,bins=50);

plt.hist(np.random.beta(2,6,size=100000),bins=50);