05wk-1: 마코프체인 (1)
2023-03-30
강의영상
youtube: https://youtube.com/playlist?list=PLQqh36zP38-xlV_TS7zhmYyyYNKv8np4W
확률벡터
- 확률변수와 확률벡터
- 확률변수 \(X: (\Omega,{\cal F}) \to (\mathbb{R},{\cal R})\)
- 확률벡터 \({\boldsymbol X}: (\Omega,{\cal F}) \to (\mathbb{R}^d,{\cal R}^d)\)
- 기호표현1
- 확률변수: \(X(\omega)=x\)
- 확률벡터: \({\boldsymbol X}(\omega)=(x_1,x_2,\dots,x_d)\)
여기에서 \((x_1,x_2,\dots,x_d)\)는 col-vec, row-vec 구분 없이 길이가 \(d\)인 vector 라고 생각한다. 언제든 편의에 따라 row-vector 혹은 col-vector로 해석할 수 있다.
- 기호표현2
- 확률변수 \(X\)
- 확률벡터 \({\boldsymbol X}=(X_1,X_2,\dots,X_d)\), 여기에서 \(X_1,X_2,\dots, X_d\)는 각각 r.v.
- 기호표현3 (외우세요!!)
- \({\boldsymbol X}(\omega) = (X_1,X_2,\dots,X_d)(\omega) = \big(X_1(\omega),X_2(\omega),\dots,X_d(\omega)\big)=(x_1,x_2,\dots,x_d)\)
(예제1) 동전을 2회 던지자!
1. outcomes: \(HH, HT, TH, TT\)
2. sample space: \(\Omega = \{HH, HT, TH, TT\}\)
3. event: \(\emptyset, \{HH\}, \{HT\}, \{TH\}, \{TT\}, \{HH,HT\}, \dots, \Omega\)
4. \(\sigma\)-field: \({\cal F}=2^{\Omega}\)
5. probability measure function: \(P: \Omega \to [0,1]\) such that
- \(P(\emptyset) = 0\)
- \(P(HH) = \frac{1}{4}\)
- \(P(HT) = \frac{1}{4}\)
- \(P(TH) = \frac{1}{4}\)
- \(P(TT) = \frac{1}{4}\)
- \(P(\{HH,HT\}) = \frac{1}{2}\)
- \(\dots\)
- \(P(\Omega) = 1\)
6. random vector: \(\boldsymbol{X}: \Omega \to \mathbb{R}^2\) such that
- \({\boldsymbol X}(HH) = (1,1)\)
- \({\boldsymbol X}(HT) = (1,0)\)
- \({\boldsymbol X}(TH) = (0,1)\)
- \({\boldsymbol X}(TT) = (0,0)\)
6의 다른표현들
- \({\boldsymbol X}(\omega_1) = (X_1,X_2)(\omega_1) = \big(X_1(\omega_1),X_2(\omega_1)\big) =(1,1)\)
- \({\boldsymbol X}(\omega_2) = (X_1,X_2)(\omega_2) = \big(X_1(\omega_2),X_2(\omega_2)\big) =(1,0)\)
- \({\boldsymbol X}(\omega_3) = (X_1,X_2)(\omega_3) = \big(X_1(\omega_3),X_2(\omega_3)\big) =(0,1)\)
- \({\boldsymbol X}(\omega_4) = (X_1,X_2)(\omega_4) = \big(X_1(\omega_4),X_2(\omega_4)\big) =(0,0)\)
확률벡터의 평균 (\(\star\))
확률변수의 평균
- 예제1: 동전을 던지는 예제
| \(\omega\) | \(x=X(\omega)\) | \(P(X=x)\) |
|---|---|---|
| \(\omega_1\) | \(0\) | \(\frac{1}{2}\) |
| \(\omega_2\) | \(1\) | \(\frac{1}{2}\) |
\[\therefore E(X)=\sum_{x=0}^{1}x P(X=x) = \big(0\times \frac{1}{2} + 1 \times \frac{1}{2} \big)=\frac{1}{2}(0+1)\]
- 예제2: 주사위를 던지는 예제
| \(\omega\) | \(x=X(\omega)\) | \(P(X=x)\) |
|---|---|---|
| \(\omega_1\) | \(1\) | \(\frac{1}{6}\) |
| \(\omega_2\) | \(2\) | \(\frac{1}{6}\) |
| \(\omega_3\) | \(3\) | \(\frac{1}{6}\) |
| \(\omega_4\) | \(4\) | \(\frac{1}{6}\) |
| \(\omega_5\) | \(5\) | \(\frac{1}{6}\) |
| \(\omega_6\) | \(6\) | \(\frac{1}{6}\) |
\[\therefore E(X)=\sum_{x=1}^{6}xP(X=x)=\frac{1}{6}(1+2+3+4+5+6)=3\]
확률벡터의 평균
- 예제1: 동전을 2회 던지는 예제
| \(\omega\) | \({\boldsymbol x}={\boldsymbol X}(\omega)\) | \(P({\boldsymbol X}={\boldsymbol x})\) |
|---|---|---|
| \(\omega_1\) | \(\begin{bmatrix} 0 \\ 0 \end{bmatrix}\) | \(\frac{1}{4}\) |
| \(\omega_2\) | \(\begin{bmatrix} 0 \\ 1 \end{bmatrix}\) | \(\frac{1}{4}\) |
| \(\omega_1\) | \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) | \(\frac{1}{4}\) |
| \(\omega_2\) | \(\begin{bmatrix} 1 \\ 1 \end{bmatrix}\) | \(\frac{1}{4}\) |
\[\therefore E({\boldsymbol X})=\frac{1}{4}\left(\begin{bmatrix} 0 \\ 0 \end{bmatrix}+\begin{bmatrix} 0 \\ 1 \end{bmatrix}+\begin{bmatrix} 1 \\ 0 \end{bmatrix}+\begin{bmatrix} 1 \\ 1 \end{bmatrix}\right)=\begin{bmatrix} \frac{1}{2} \\ \frac{1}{2} \end{bmatrix} = \begin{bmatrix} E(X_1)\\ E(X_2) \end{bmatrix}\]
\(E(X_1)=E(X_2)\)인 이유??
iid이니까~
- 예제2: 동전을 10회 던지는 예제
| \(\omega\) | \({\boldsymbol x}={\boldsymbol X}(\omega)\) | \(P({\boldsymbol X}={\boldsymbol x})\) |
|---|---|---|
| \(\omega_1\) | \([0,0,\dots,0]^\top\) | \(\frac{1}{2^{10}}\) |
| \(\omega_2\) | \([0,0,\dots,1]^\top\) | \(\frac{1}{2^{10}}\) |
| \(\dots\) | \(\dots\) | \(\dots\) |
| \(\omega_{1024}\) | \([1,1,\dots,1]^\top\) | \(\frac{1}{2^{10}}\) |
\[\therefore E({\boldsymbol X})=\begin{bmatrix} \frac{1}{2} \\ \frac{1}{2} \\ \dots \\ \frac{1}{2} \end{bmatrix} = \begin{bmatrix} E(X_1)\\ E(X_2) \\ \dots \\ E(X_{10}) \end{bmatrix}\]
시간평균, 앙상블평균
motivating example
- 예제1: 동전을 1000번 던지는 예제를 상상하자. 앞면이 나올 확률은 \(p\)이며 이 \(p\)는 0.5인지 모른다고 가정하자.
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0,
1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1,
1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0,
0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0,
1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1,
1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1,
1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0,
1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0,
1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1,
1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1,
1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1,
1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1,
1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1,
1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1,
1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0,
1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0,
1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1,
1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1,
0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1,
1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1,
1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0,
1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0,
0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0,
1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1,
1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1,
1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1,
1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0,
0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1,
1, 1, 1, 0, 1, 1, 1, 0, 1, 1])- 이것은 적당한 \(\omega\)에 맵핑되어있는 하나의 realization 이다.
- 질문: unknown_probability는 얼마일까??
- 비판: 문제 이상하게 푼다?
| \(\omega\) | \({\boldsymbol x}={\boldsymbol X}(\omega)\) | \(P({\boldsymbol X}={\boldsymbol x})\) |
|---|---|---|
| \(\omega_1\) | \([0,0,\dots,0]^\top\) | \(\frac{1}{2^{1000}}\) |
| \(\omega_2\) | \([0,0,\dots,1]^\top\) | \(\frac{1}{2^{1000}}\) |
| \(\dots\) | \(\dots\) | \(\dots\) |
| \(\omega_{2^{1000}}\) | \([1,1,\dots,1]^\top\) | \(\frac{1}{2^{1000}}\) |
\[\therefore E({\boldsymbol X})= \begin{bmatrix} E(X_1)\\ E(X_2) \\ \dots \\ E(X_{1000}) \end{bmatrix}\]
- \(E(X_{1000})=\frac{1}{2^{1000}}\big(\text{대충 0 혹은 1이 있는 숫자들을 더한것}\big)=p\)
따라서 개념상으로는 아래와 같이 시뮬레이션하여 구하는게 옳음
sample1 = np.random.binomial(n=1,p=unknown_probability,size=1000)
sample2 = np.random.binomial(n=1,p=unknown_probability,size=1000)
sample3 = np.random.binomial(n=1,p=unknown_probability,size=1000)
sample4 = np.random.binomial(n=1,p=unknown_probability,size=1000)
sample5 = np.random.binomial(n=1,p=unknown_probability,size=1000)
sample6 = np.random.binomial(n=1,p=unknown_probability,size=1000)
sample7 = np.random.binomial(n=1,p=unknown_probability,size=1000) 0.8571428571428571좀 더 많이…
용어정리의 시간
- 확률변수열을 표현할 때 \(i\)대신 \(t\)로 바꾼다면?
- \(X_1,X_2,X_3,\dots, X_i, \dots, X_n\) \(\Rightarrow\) \(X_1,X_2,X_3\dots,X_t,\dots X_T\)
- \(E(X_i)\) \(\Rightarrow\) \(E(X_t)\)
- \(\frac{1}{n}\sum_{i=1}^{n}X_i\) \(\Rightarrow\) \(\frac{1}{T}\sum_{t=1}^{T}X_t\)
- 용어: \(E(X_t)\)를 앙상블평균 (ensemble average) 이라고 하고, \(\frac{1}{T}\sum_{t=1}^{T}X_t\)를 시간평균 (time average) 이라고 한다.
생각의 시간 (1)
- 원래 \(E(X_{1000})\)은 \(\frac{1}{T}\sum_{t=1}^{T}X_t\)와 같은 방식으로 근사계산할 수 없긴해. (말도 안되는 소리임..)
- 예제1: 아래와 같은 확률변수열를 고려하자.
- \(X_1 \sim Ber(0.5)\).
- \(X_t= X_{t-1}\) for \(t=2,3,4,\dots, 1000\).
\(E(X_{1000})\)을 구하여라. \(E(X_{1000})\)을 \(\frac{1}{T}\sum_{t=1}^T X_t\)와 같은 방식으로 근사할 수 있는가?
(풀이)
\(E(X_{1000})=0.5\)임. 하지만 \(\frac{1}{T}\sum_{t=1}^{T}X_t\)로 \(E(X_{1000})\)을 근사할 수 없음.
시뮬1 – calculating time average of one-sample \((x_1,\dots,x_{1000})\)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0])시뮬2 – approximating ensemble average with 43052 samples
samples = np.array([[np.random.binomial(n=1,p=0.5,size=1).item()] * 1000 for i in range(43052)])
samples array([[1, 1, 1, ..., 1, 1, 1],
[0, 0, 0, ..., 0, 0, 0],
[1, 1, 1, ..., 1, 1, 1],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[1, 1, 1, ..., 1, 1, 1]])- 하지만 사실 iid가정이 있다면 앙상블평균을 시간평균으로 추정해도 문제 없어.
- 예제2: 서로 독립인 1000개의 확률변수를 \(N(0,1)\)에서 뽑는다고 하자.
- \(X_t=\epsilon_t \overset{i.i.d.}{\sim} N(0,1)\)
이때는 \(E(X_{1000})\)을 \(\frac{1}{T}\sum_{t=1}^T X_t\)와 같은 방식으로 근사할 수 있다.
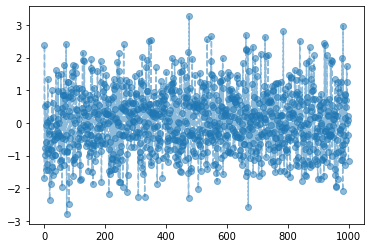
시뮬1 – calculating time average of one-sample \((x_1,\dots,x_{1000})\)
시뮬2 – approximating ensemble average with 43052 samples
- 결론: 원래 time-average와 ensemble-average는 “전혀” 다른 개념이다. 그런데, 확률변수열이 iid일 경우는 time-average로 ensemble-average를 근사계산 할 수 있다.
- 아래의 그림은 time-average와 ensemble-average의 차이를 파악하기 용이한 예제이다.
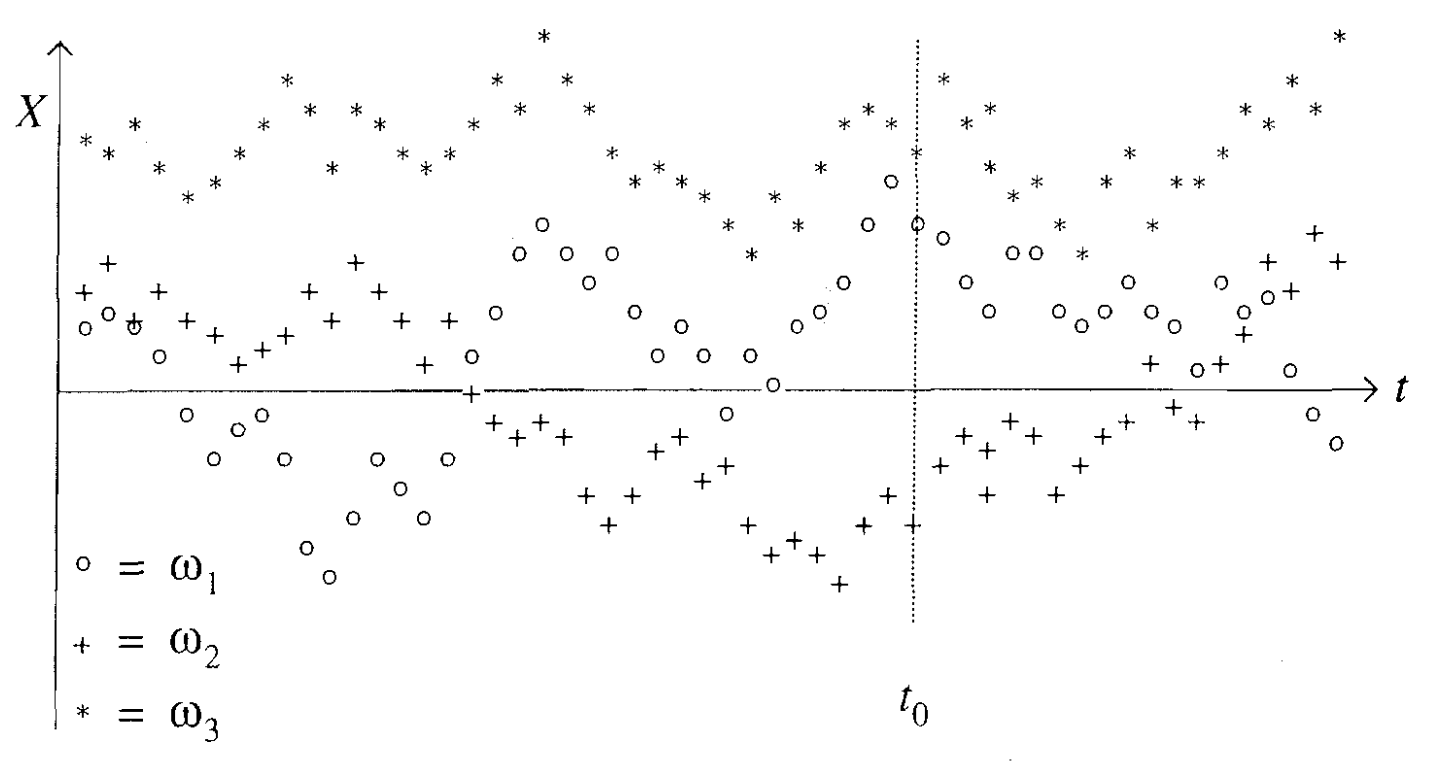
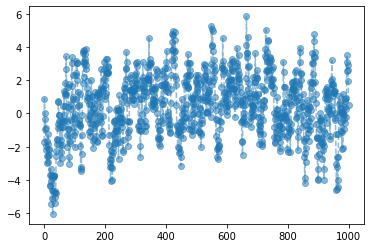
AR(1)
- 예제3: \(\epsilon_t \overset{i.i.d.}{\sim} N(0,1)\) 일 때, 아래와 같은 확률변수 열을 고려하자.
- \(X_1=\epsilon_1\)
- \(X_t=\frac{7}{8}X_{t-1} + \epsilon_t\) for \(t=2,3,\dots,T\)
이때 \(E(X_{T})\)을 \(\frac{1}{T}\sum_{t=1}^T X_t\)와 같은 방식으로 근사할 수 있을까?
(풀이)
우선 독립인지 아닌지 체크해보자.
check: \(X_t\)와 \(X_{t-1}\)은 독립??
- corr이 있음.. \(\Rightarrow\) 독립아님 \(\Rightarrow\) ensemble-average를 time-average로 근사할 수 없다??
참고로 독립이라면~
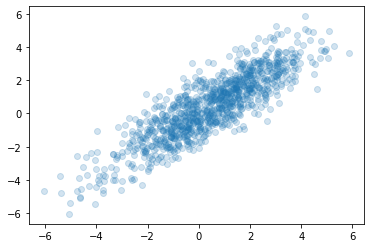
시뮬1 – calculating time average of one-sample \((x_1,\dots,x_{T})\)
시뮬2 – approximating ensemble average with 43052 samples
근사 되는 것 같은데..?
생각의 시간 (2)
- 확률변수는 값이 랜덤으로 바뀌는 변수느낌이 아니라 \(X: \Omega \to \mathbb{R}\) 인 잴 수 있는 함수임.
- 확률벡터는 값이 랜덤으로 바뀌는 벡터느낌이 아니라 \(X: \Omega \to \mathbb{R}^d\) 인 잴 수 있는 함수임.
- 동전을 반복하여 던져서 관측한 아래와 같은 확률변수열(=확률벡터)
\[0,1,0,0,1,1,\dots,1\]
은 어떠한 \(\omega \in \Omega\)에 대응하는 하나의 realization \({\boldsymbol X}(\omega)={\boldsymbol x}\) 임. (즉 one-sample임)
- 그런데 확률변수열을 독립으로 얻었다면 이러한 one-sample을 쪼개서 마치 여러개의 샘플을 얻은것처럼 생각할 수 있으며 이때
\[E(X_T)\approx \frac{1}{T}\sum_{t=1}^{T}X_t\]
와 같은 방식으로 근사할 수 있음.
- 사실상 \(E(X_1)=E(X_2)=\dots=E(X_T) \approx \frac{1}{T}\sum_{t=1}^{T}X_t\) 이므로 (\(\because\) iid) 결국 아직 관측되지 않은 미래시점 \(T+1\)의 값에 대해서도
\[E(X_{T+1}) \approx \frac{1}{T}\sum_{t=1}^T X_t\]
라고 주장할 수 있음.
- 이렇게 one-sample을 여러개의 조각으로 쪼개는 기법은 iid에서만 성립할 것 같음. 만약에 iid가정이 없다면 (시뮬2)와 같은 방식으로 여러샘플을 통하여 ensemble-average를 근사시켜야 함. 정리하면 아래와 같음.
- one-sample만 관측가능, iid 조건 만족 \(\Rightarrow\) 분석가능
- 여러개의 sample 관측가능 , iid 조건 만족 \(\Rightarrow\) 분석가능
- one-sample만 관측가능, iid 조건 만족하지 않음 \(\Rightarrow\) 분석불가능??
- 여러개의 sample 관측가능 , iid 조건 만족하지 않음 \(\Rightarrow\) 분석가능
- 문제: 그런데 실제로 우리가 다루고 싶은 자료의 형태는 3의 경우가 많다.
- 소망: 그래서 iid가 아니지만 마치 iid인것 처럼 one-sample을 가지고 분석하고 싶다.
앞으로 해야 할 것: 독립인듯 독립아닌 독립같은 확률과정은 없을까?
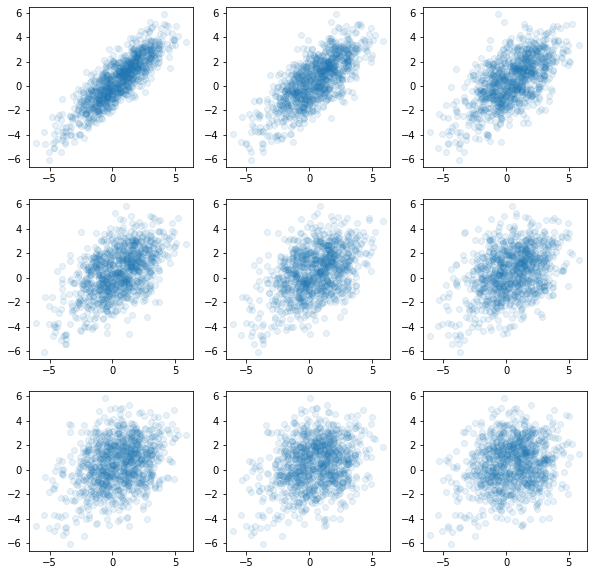
독립인듯 독립아닌 독립같은 확률과정
fig, ax = plt.subplots(3,3,figsize=(10,10))
ax[0][0].plot(x[:-1],x[1:],'o',alpha=0.1)
ax[0][1].plot(x[:-2],x[2:],'o',alpha=0.1)
ax[0][2].plot(x[:-3],x[3:],'o',alpha=0.1)
ax[1][0].plot(x[:-4],x[4:],'o',alpha=0.1)
ax[1][1].plot(x[:-5],x[5:],'o',alpha=0.1)
ax[1][2].plot(x[:-6],x[6:],'o',alpha=0.1)
ax[2][0].plot(x[:-7],x[7:],'o',alpha=0.1)
ax[2][1].plot(x[:-8],x[8:],'o',alpha=0.1)
ax[2][2].plot(x[:-9],x[9:],'o',alpha=0.1)