03wk-1: 측도론 intro (3)
2023-03-16
강의영상
https://youtube.com/playlist?list=PLQqh36zP38-y_-OXU_IFt6uH3oo61swW4
지난시간 내용
전사, 단사, 전단사
함수 \(f: X \to Y\) 를 상상하자.
- 단사함수(일대일함수,인젝티브한 함수): \(\forall x_1,x_2 \in X: ~ x_1 \neq x_2 \Rightarrow f(x_1)\neq f(x_2)\)
- 암기 (고등학교): 입력이 다르면 출력이 달라
- 느낌: 화살표가 팍 퍼지는 느낌
- 그래프를 이용한 판단 (고등학교): 수평선을 그어서 교점이 2개 이상이면 단사함수가 아님
- 전사함수(위로의함수,서젝티브한 함수): \(\forall y \in Y~ \exists x \in X\) such that \(f(x)=y\)
- 암기 (고등학교): 치역 = 공역
- 암기 (대학교): inverse image가 정의역에 있어야함 (\(\star\))
- 느낌: 화살표가 모이는 느낌
- 그래프를 이용한 판단 (고등학교): 모양으로 판단하기 애매함..1
1 \(y=x^2\)은 공역을 \(\mathbb{R}\)로 설정한다면 전사함수가 아니지만 공역을 \(\mathbb{R}_{\geq 0}\)로 설정한다면 전사함수임
- 전단사함수(일대일대응함수,바이젝티브한 함수)
예제 (finite cases)
예시1
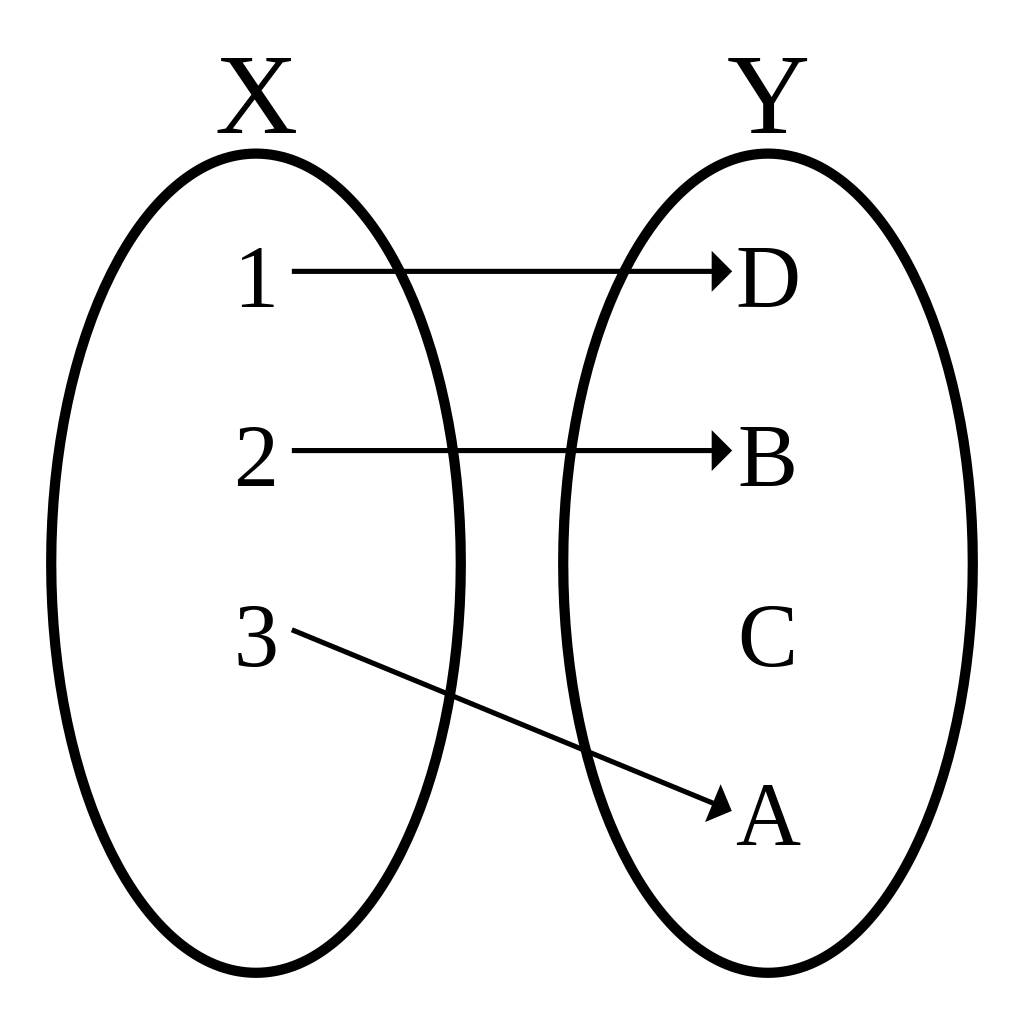
- 단사함수임을 따져보자!
\(\forall x_1,x_2 \in X: x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2)\)
| \(x_1\) | \(x_2\) | \(f(x_1)\) | \(f(x_2)\) |
|---|---|---|---|
| 1 | 2 | D | B |
| 1 | 3 | D | A |
| 2 | 1 | B | D |
| 2 | 3 | B | A |
| 3 | 1 | A | D |
| 3 | 2 | A | B |
- 전사함수임을 따져보자!
\(\forall y \in Y ~ \exists x \in X\) such that \(f(x)=y\)
| \(y\) | \(x\) such that \(f(x)=y\) |
|---|---|
| D | 1 |
| B | 2 |
| C | ? |
| A | 3 |
예시2
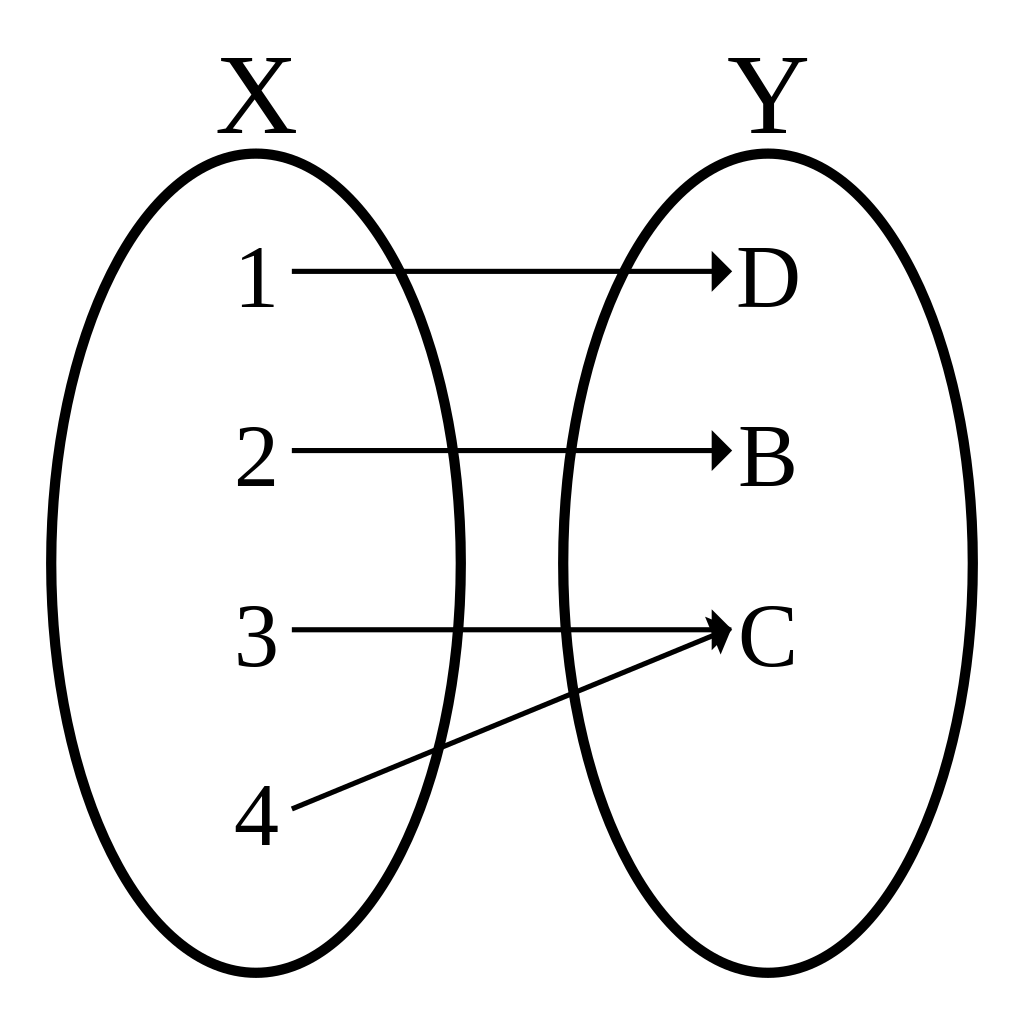
- 단사함수임을 따져보자!
\(\forall x_1,x_2 \in X: x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2)\)
| \(x_1\) | \(x_2\) | \(f(x_1)\) | \(f(x_2)\) |
|---|---|---|---|
| 1 | 2 | D | B |
| 1 | 3 | D | C |
| 1 | 4 | D | C |
| 2 | 1 | B | D |
| 2 | 3 | B | C |
| 2 | 4 | B | C |
| 3 | 1 | C | D |
| 3 | 2 | C | B |
| 3 | 4 | C | C |
| 4 | 1 | C | D |
| 4 | 2 | C | B |
| 4 | 3 | C | C |
- 전사함수임을 따져보자!
\(\forall y \in Y ~ \exists x \in X\) such that \(f(x)=y\)
| \(y\) | \(x\) such that \(f(x)=y\) |
|---|---|
| D | 1 |
| B | 2 |
| C | 3,4 |
예시3

- 단사함수임을 따져보자!
\(\forall x_1,x_2 \in X: x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2)\)
| \(x_1\) | \(x_2\) | \(f(x_1)\) | \(f(x_2)\) |
|---|---|---|---|
| 1 | 2 | d | d |
| 1 | 3 | d | c |
| 2 | 1 | d | d |
| 2 | 3 | d | c |
| 3 | 1 | c | d |
| 3 | 2 | c | d |
- 전사함수임을 따져보자!
\(\forall y \in Y ~ \exists x \in X\) such that \(f(x)=y\)
| \(y\) | \(x\) such that \(f(x)=y\) |
|---|---|
| a | ? |
| d | 1,2 |
| b | ? |
| c | 3 |
예제 (infinite cases)
예시1
- 아래를 판단해보자.
\(f:\mathbb{R} \to \mathbb{R}\) defined by \(f(x)=2x+1\). // 답2
\(f:\mathbb{R} \to \mathbb{R}\) defined by \(f(x)=x^2\). // 답3
\(f:\mathbb{R} \to \mathbb{R}_{\geq 0}\) defined by \(f(x)=x^2\). // 답4
\(f:\mathbb{Z} \to \{0,1\}\) defined by \(f(x)= x ~\text{mod}~ 2\). // 답5
\(f:\mathbb{N} \to \mathbb{N} \cup \{0\}\) defined by \(f(x)= x-1\). // 답6
\(f:\mathbb{N} \to \mathbb{N}^-\) defined by \(f(k)= -k\). // 답7
- 여기에서 \(\mathbb{N}^-\{-1,-2,\dots,\}\) 으로 정의
2 단사 O, 전사 O
3 단사 X, 전사 X
4 단사 X, 전사 O
5 단사 X, 전사 O
6 단사 O, 전사 O
7 단사 O, 전사 O
예시2
- 집합 \(X\)가 집합 \(Y\)의 부분집합이라면 항상 \(X\)에서 \(Y\)로 향하는 단사함수가 존재함을 보여라.
- 따라서 \(X \subset Y\) \(\Rightarrow\) \(|X|\leq |Y|\)
실수집합의 카디널리티
- 아래의 관계가 성립했다.
- \(|\mathbb{N}| = \aleph_0\)
- \(|\mathbb{N}\cup \{0\}| = \aleph_0\)
- \(|\mathbb{Z}| = \aleph_0\)
- \(|\mathbb{Q}| = \aleph_0\)
- 그렇다면 아래는 어떠할까?
\[|\mathbb{R}|=??\]
(주장) 실수의 유리수의 카디널넘버 보다 크다.
그런데 유리수의 카디널넘버와 자연수의 카디널넘버가 같다는 것을 떠올리면 “실수의 카디널넘버는 자연수의 카디널넘버보다 크다” 를 보여도 충분함을 유추할 수 있다.
(단사)
자연수에서 실수로 가는 단사함수는 존재한다. (자연수는 실수의 부분집합이니까)
(전사)
소망: \(\mathbb{N}\)에서 \(\mathbb{R}\)로 향하는 전사는 존재할 수 없음을 보이고 싶음.
소망2: 그런데 \(\mathbb{N}\)에서 \([0,1]\)로 향하는 전사가 존재할 수 없음을 보여도 충분함.
전략: \(\mathbb{N}\)에서 \([0,1]\)로 가는 전사가 존재한다고 가정하고 모순을 이끌어 내자.
1. 아래와 같은 주장을 하는 가상의 인물을 세움:
\(\mathbb{N}\)에서 \([0,1]\)로 향하는 전사함수가 존재한다.
2. 그 가상의 인물이 하는 주장을 잘 생각해보면 아래와 같음
\(f\)는 정의역이 자연수이고 공역이 실수인 함수이므로 아래와 같은 형태일 것임.
- \(f(1)=0.2344253456\cdots\)
- \(f(2)=0.3459837981\cdots\)
- \(f(3)=0.5452349871\cdots\)
- \(\dots\)
그 가상의 인물의 주장대로라면
\[[0,1]=\{f(1),f(2),f(3),\dots\}\]
이라는 의미임.8
8 다시 말하면 \([0,1]\) 사이의 모든 실수는 “셀수있다”라는 의미임
3. 전사함수의 정의에 의하여 아래가 성립해야 함
\(\forall y\in [0,1] ~\exists x \in \mathbb{N}\) such that \(f(x)=y\)
아래의 원리에 따라서 \(y=0.x_1x_2x_3\cdots\)를 뽑는다면?
- \(y\)의 첫번째 소수점의 값 \(x_1\)은 \(f(1)\)의 첫번째 소수점과 다르게 한다. \(\Rightarrow\) \(y\neq f(1)\) \(\Rightarrow\) \(y \notin \{f(1)\}\)
- \(y\)의 두번째 소수점의 값 \(x_2\)은 \(f(2)\)의 두번째 소수점과 다르게 한다. \(\Rightarrow\) \(y\neq f(1)\) and \(y\neq f(2)\) \(\Rightarrow\) \(y \notin \{f(1), f(2)\}\)
이러한 \(y\)는 분명히 실수이지만 \(y \notin \{f(1),f(2),f(3),\dots,\}\) 이다.9
9 모순이네?
무리수집합의 카디널리티
(주장) 무리수집합의 카디널리티는 \(\aleph_0\)가 아니다.
(쉐도복싱) 무리수집합의 카디널리티가 \(\aleph_0\) 이라고 하자.
- \(\mathbb{R} = \mathbb{Q} \cup \mathbb{Q}^c\)
- \(|\mathbb{Q}|=\aleph_0\) 이므로 \(\mathbb{Q}\)와 \(\mathbb{N}\)사이에는 전단사함수가 존재함.
- \(|\mathbb{Q}^c|=\aleph_0\) 이므로 \(\mathbb{Q}^c\)와 \(\mathbb{N}^{-}=\{-1,-2,\dots\}\)사이에는 전단사함수가 존재함.
- 따라서 \(\mathbb{Q} \cup \mathbb{Q}^c\) 와 \(\mathbb{N} \cup \mathbb{N}^-\) 사이에는 전단사함수가 존재함. (모순)