07wk-1: Numpy 활용 (1)

Author

최규빈

Published

April 17, 2023

강의영상

youtube: https://youtube.com/playlist?list=PLQqh36zP38-wp6tJXCOxllNM6aqdYEpkT

강의영상 재촬영하여 업로드했습니다.

import

import numpy as np

예비학습: matplotlib

import matplotlib.pyplot as plt

line plot

기본플랏

- 예시1

x=[1,2,3,4]
y=[1,2,4,3]

plt.plot(x,y)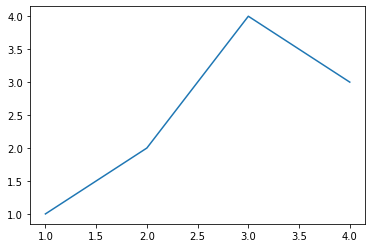

모양변경

- 예시1

plt.plot(x,y,'--')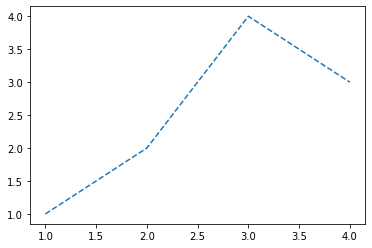

- 예시2

plt.plot(x,y,':')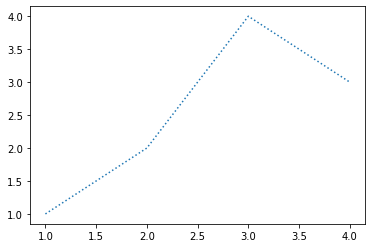

- 예시3

plt.plot(x,y,'-.')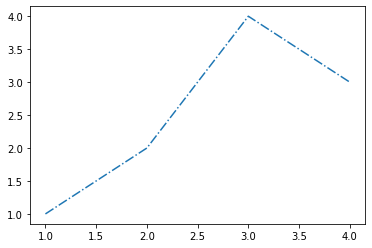

색상변경

- 예시1

plt.plot(x,y,'r')

- 예시2

plt.plot(x,y,'k')

모양 + 색상변경

- 예시1

plt.plot(x,y,'--r')

- 예시2: 순서변경 가능

plt.plot(x,y,'r--')

원리? (\(\star\))

- r--등의 옵션은 Markers + Line Styles + Colors 의 조합으로 표현가능

ref: https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html

--r: 점선(dashed)스타일 + 빨간색
r--: 빨간색 + 점선(dashed)스타일
:k: 점선(dotted)스타일 + 검은색
k:: 검은색 + 점선(dotted)스타일

- 우선 Marker를 무시하면 Line Styles + Color로 표현가능한 조합은 \(4\times 8=32\) 개

(Line Styles) 모두 4개

character	description
‘-’	solid line style
‘–’	dashed line style
‘-.’	dash-dot line style
‘:’	dotted line style

(Color) 모두 8개

character	color
‘b’	blue
‘g’	green
‘r’	red
‘c’	cyan
‘m’	magenta
‘y’	yellow
‘k’	black
‘w’	white

scatter plot

기본플랏

- 예시1

plt.plot(x,y,'o')

- 예시2

plt.plot(x,y,'.')

- 예시3

plt.plot(x,y,'x')

색깔변경

- 예시1

plt.plot(x,y,'or')

- 예시2

plt.plot(x,y,'db')

- 예시3

plt.plot(x,y,'bx')

dot-connected plot

- 예시1: 마커와 라인스타일을 동시에 사용하면 dot-connected plot이 된다.

plt.plot(x,y,'o-')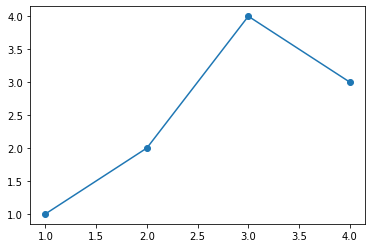

- 예시2: 당연히 색도 적용가능함

plt.plot(x,y,'o--r')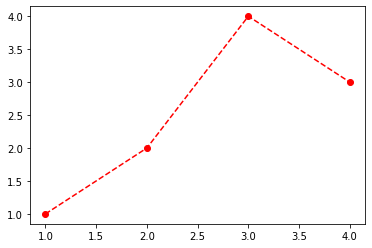

- 예시3: 서로 순서를 바꿔도 상관없다.

plt.plot(x,y,'ro--')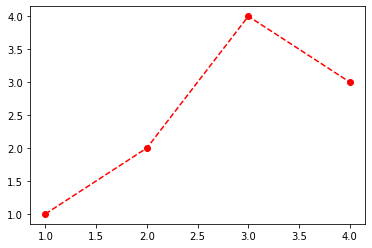

겹쳐그리기

- 예시1

x = np.arange(-5,5,0.1)
ϵ = np.random.randn(100) 
y = 2*x + ϵ

plt.plot(x,y,'.')
plt.plot(x,2*x,'--')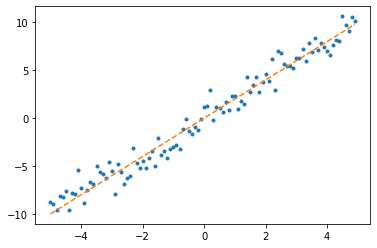

이미지자료의 이해 및 시각화

- 참고: 빛의삼원색

- 이미지자료의 이해: 이미지자료는 rgb값이 저장된 3개의 매트릭스를 쌓은것이라 이해가능

이미지자료의 shape은 (가로픽셀, 세로픽셀, 3) 이다. // 5*5 이미지라면 (5,5,3)
3은 RGB 빛의 밝기를 정의함.
밝기는 0-255 사이의 int, 0-1 사이의 float으로 정한다.
int 255 혹은 float 1 은 해당색이 매우 밝다는 것을 의미함.
각 픽셀의 색깔은 RGB의 밝기 (RGB의 값) 으로 조정가능하다. (따라서 총 256256256 개의 색상을 표현할 수 있다.)

- 예시1

r = np.array([0]*25*3).reshape(5,5,3) 
g = np.array([0]*25*3).reshape(5,5,3) 
b = np.array([0]*25*3).reshape(5,5,3)

r[:3,:3,0] = 255

r[:3,:3,0] = 255   
g[:3,2:,1] = 255
b[2:,:,2] = 255

r[:,:,0], r[:,:,1], r[:,:,2]

(array([[255, 255, 255,   0,   0],
        [255, 255, 255,   0,   0],
        [255, 255, 255,   0,   0],
        [  0,   0,   0,   0,   0],
        [  0,   0,   0,   0,   0]]),
 array([[0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0]]),
 array([[0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0]]))

g[:,:,0], g[:,:,1], g[:,:,2]

(array([[0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0]]),
 array([[  0,   0, 255, 255, 255],
        [  0,   0, 255, 255, 255],
        [  0,   0, 255, 255, 255],
        [  0,   0,   0,   0,   0],
        [  0,   0,   0,   0,   0]]),
 array([[0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0]]))

b[:,:,0], b[:,:,1], b[:,:,2]

(array([[0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0]]),
 array([[0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0]]),
 array([[  0,   0,   0,   0,   0],
        [  0,   0,   0,   0,   0],
        [255, 255, 255, 255, 255],
        [255, 255, 255, 255, 255],
        [255, 255, 255, 255, 255]]))

plt.imshow(r+g+b)

<matplotlib.image.AxesImage at 0x7f6a94cdd6a0>

- 예시2: r,g,b에 작은 숫자를 주면 점점 어두워 진다.

r = np.array([0]*25*3).reshape(5,5,3) 
g = np.array([0]*25*3).reshape(5,5,3) 
b = np.array([0]*25*3).reshape(5,5,3)

r[:3,:3,0] = 80
g[:3,2:,1] = 80
b[2:,:,2] = 80

plt.imshow((r+g+b))

<matplotlib.image.AxesImage at 0x7f6a94c52040>

- 예시3: r,g,b 값이 float으로 저장되었다면 표준화가 진행된것으로 컴퓨터가 이해한다.

r = np.array([0]*25*3).reshape(5,5,3) 
g = np.array([0]*25*3).reshape(5,5,3) 
b = np.array([0]*25*3).reshape(5,5,3)

r[:3,:3,0] = 1
g[:3,2:,1] = 1
b[2:,:,2] = 1

plt.imshow(r+g+b)

<matplotlib.image.AxesImage at 0x7f6a94b044f0>

plt.imshow((r+g+b)*1.0) # array의 각 원소의 자료형이 float이면 표준화된 자료라고 이해하고 칼라스케일을 다시 맞춰줌.

<matplotlib.image.AxesImage at 0x7f6a949e03a0>

plt.imshow((r+g+b)*2.0) # 2.0을 곱해도 출력하긴 해줌.. (경고메시지 발생)

Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).

<matplotlib.image.AxesImage at 0x7f6a949c9790>

넘파이 활용 (1단계)

그래프

1. \(y(t)=\cos(2t)\)와 \(x(t)=\sin(t)\)를 고려하자. \(y(t)=x(t)\)는 \(-3.14\leq t \leq 3.14\) 에서 몇 개의 해를 가지는가? 그래프를 통하여 확인하라.

(풀이)

t = np.linspace(-3.14,3.14,1000)
y = np.cos(2*t)
x = np.sin(t)

plt.plot(t,x)
plt.plot(t,y)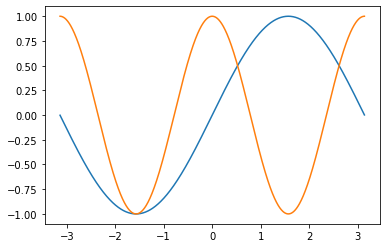

2-3. 아래와 같은 합성함수를 생각하라.

\(l(x)=w_0+w_1x\)
\(a(x)=\frac{1}{1+e^{-x}}\)

2. \(x \in [-5,5]\)의 범위에서 \(a(l(x))\)의 그래프를 그려라. 단 이때 \(w_0=0, w_1=1\)로 설정한다.

(풀이)

\(y=a(l(x))= a(w_0+w_1x) = 1/(1+\exp(-w_0-w_1x))\)

그런데, \(w_0=0\) 이고 \(w_1=1\) 이므로 \(y=a(l(x)) = 1/ (1+\exp(-x))\) 이다.

x = np.linspace(-5,5,100)
y = 1/(1+np.exp(-x))
plt.plot(x,y)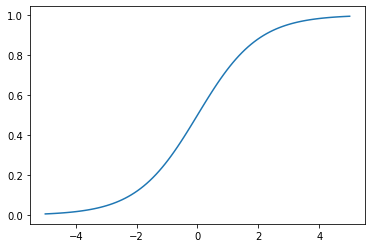

3. 아래는 \(a(l(x))\)의 성질에 대하여 토의한 내용이다. 올바르게 서술한 학생을 골라라.

하영: \(w_0=0,w_1=1\) 이면 \(a(l(x))\)는 증가하는 함수이다.
재인:
서연:
보람:
지윤:

(풀이)

아래와 같은 함수를 선언한뒤에 하나씩 체크해 나가면된다.

def l(x,w0=0,w1=1): 
    return w0+w1*x 
def a(x): 
    return 1/(1+np.exp(-x))

자료를 저장하는 행렬

- 제 생각: 통계학과에서 매트릭스를 바라볼때 2가지중 하나로 봐야한다.

데이터를 저장하는 관점에서의 행렬: \(X_{n\times p}\)인 정형자료, \(X\)가 이미지자료
데이터를 변환하는 관점에서의 행렬: 선형변환 (회전변환, 평균을 구하는 행렬 등)

data=[70,80,75,85,95]
trans = [1/5]*5

np.array(data) @ np.array(trans)

81.0

sum(data)/5

81.0

1-2. 아래와 같은 자료를 관측하였다고 하자.

X = np.array([[11.75 ,  5.72 ],
              [12.39 ,  7.695],
              [11.75 ,  6.93 ],
              [11.625,  4.195],
              [12.6  ,  6.734],
              [11.13 ,  6.688],
              [12.24 ,  7.33 ],
              [13.586,  1.072],
              [10.9  ,  4.125],
              [10.68 ,  3.691]])

1. X를 평균과 표준편차를 columnwise 하게 구하라. 즉 1열의 평균, 2열의 평균, 1열의 표준편차, 2열의 표준편차를 구하라.

note: 표준편차는 ddof=1과 함께 np.std()를 사용할 것

(풀이)

X.mean(axis=0)

array([11.8651,  5.418 ])

X.std(ddof=1,axis=0)

array([0.87420064, 2.09762829])

2. X를 columnwise 하게 표준화하라.

hint: np.apply_along_axis의 함수의 기능을 관찰하고 이용하라.

(예시1)

X.mean(axis=0)

array([11.8651,  5.418 ])

X.mean(axis=0), np.apply_along_axis(np.mean,axis=0,arr=X)

(array([11.8651,  5.418 ]), array([11.8651,  5.418 ]))

(예시2)

def f(arr):
    return arr - np.min(arr) 
X, np.apply_along_axis(f,axis=0,arr=X)

(array([[11.75 ,  5.72 ],
        [12.39 ,  7.695],
        [11.75 ,  6.93 ],
        [11.625,  4.195],
        [12.6  ,  6.734],
        [11.13 ,  6.688],
        [12.24 ,  7.33 ],
        [13.586,  1.072],
        [10.9  ,  4.125],
        [10.68 ,  3.691]]),
 array([[1.07 , 4.648],
        [1.71 , 6.623],
        [1.07 , 5.858],
        [0.945, 3.123],
        [1.92 , 5.662],
        [0.45 , 5.616],
        [1.56 , 6.258],
        [2.906, 0.   ],
        [0.22 , 3.053],
        [0.   , 2.619]]))

(풀이)

def f(arr): 
    return (arr-arr.mean()) / arr.std(ddof=1)

np.apply_along_axis(f,axis=0,arr=X)

array([[-0.13166314,  0.14397212],
       [ 0.60043424,  1.08551168],
       [-0.13166314,  0.72081408],
       [-0.27465091, -0.58303943],
       [ 0.84065369,  0.62737522],
       [-0.84088247,  0.60544569],
       [ 0.42884892,  0.91150563],
       [ 1.96854122, -2.07186374],
       [-1.10397997, -0.61641045],
       [-1.35563844, -0.82331079]])

3-5. 아래는 이미지파일을 불러오는 코드이다.

import PIL

!wget https://raw.githubusercontent.com/guebin/SC2022/main/hani.jpeg
hani = np.einsum('ijk->jik',np.array(PIL.Image.open('hani.jpeg'),dtype=np.int64)/255)
!rm hani.jpeg

note: 위 코드는 코랩 혹은 리눅스기반 환경에서 동작가능.
주피터노트북의 경우 아래의 절차를 따를 것
1. https://raw.githubusercontent.com/guebin/SC2022/main/hani.jpeg 에서 직접사진을 다운로드
2. 현재작업중인 주피터노트북과 같은폴더에 그림파일을 옮김
3. hani = np.einsum('ijk->jik',np.array(PIL.Image.open('hani.jpeg'),dtype=np.int64)/255) 실행 // 그전에 import PIL 을 해야함
4. 그림파일 삭제

불러온 이미지는 아래와 같다.

hani,hani.shape

(array([[[0.44705882, 0.48627451, 0.49411765],
         [0.43137255, 0.46666667, 0.48627451],
         [0.45882353, 0.50196078, 0.51764706],
         ...,
         [0.6627451 , 0.6627451 , 0.70196078],
         [0.63529412, 0.62745098, 0.67058824],
         [0.64313725, 0.63529412, 0.67843137]],
 
        [[0.45882353, 0.49803922, 0.50588235],
         [0.44313725, 0.47843137, 0.49803922],
         [0.4627451 , 0.50588235, 0.52156863],
         ...,
         [0.63921569, 0.63921569, 0.67843137],
         [0.64313725, 0.63529412, 0.67843137],
         [0.63137255, 0.62352941, 0.66666667]],
 
        [[0.45490196, 0.49411765, 0.50196078],
         [0.4627451 , 0.49803922, 0.51764706],
         [0.45882353, 0.50196078, 0.51764706],
         ...,
         [0.64313725, 0.64313725, 0.68235294],
         [0.65490196, 0.65490196, 0.69411765],
         [0.64705882, 0.63921569, 0.68235294]],
 
        ...,
 
        [[0.69411765, 0.69803922, 0.70588235],
         [0.68627451, 0.69019608, 0.69803922],
         [0.69411765, 0.69803922, 0.70588235],
         ...,
         [0.60784314, 0.6       , 0.60392157],
         [0.6       , 0.59215686, 0.59607843],
         [0.59607843, 0.58823529, 0.59215686]],
 
        [[0.70196078, 0.70588235, 0.71372549],
         [0.72156863, 0.7254902 , 0.73333333],
         [0.69019608, 0.69411765, 0.70196078],
         ...,
         [0.61176471, 0.60392157, 0.60784314],
         [0.60392157, 0.59607843, 0.6       ],
         [0.61568627, 0.60784314, 0.61176471]],
 
        [[0.7254902 , 0.72941176, 0.74509804],
         [0.73333333, 0.7372549 , 0.74509804],
         [0.70980392, 0.71372549, 0.72156863],
         ...,
         [0.61176471, 0.60392157, 0.60784314],
         [0.60392157, 0.59607843, 0.6       ],
         [0.61960784, 0.61176471, 0.61568627]]]),
 (4032, 3024, 3))

이미지는 4032 \(\times\) 3024 개의 격자(픽셀)로 이루어져 있음

이미지를 보는 방법은 아래와 같다.

plt.imshow(hani) # 모든이미지, 하니매트릭스

<matplotlib.image.AxesImage at 0x7f6a956ed9d0>

plt.imshow(hani[1000:1500, 1000:2000,:]) # 얼굴만 확대, 하니의 서브매트릭스

<matplotlib.image.AxesImage at 0x7f6a94572f10>

3. 하니이미지를 나타내는 어레이를 변형하여 빨간색을 의미하는 칼라만 남겨서 “빨간하니”를 만들고 이미지를 출력하라.

(풀이)

red_hani = hani*0 
red_hani[:,:,0] = hani[:,:,0]
plt.imshow(red_hani)

<matplotlib.image.AxesImage at 0x7f6a91b1d5e0>

4. 하니의 모든 값에 루트를 취하여 “루트하니”를 만들고 “원본하니”와 “루트하니”를 좌우로 나란히 배치하여 출력하라.

(풀이)

root_hani = np.sqrt(hani)
plt.imshow(np.concatenate([hani,root_hani],axis=1))

<matplotlib.image.AxesImage at 0x7f6a933b7910>

“루트하니”의 이미지는 “원본하니”의 이미지와 비교하여 어떤가? 왜 그러한 결과가 나왔다고 생각하는가?

5. 하니의 모든값에 아래와 같은 함수를 적용하라.

\(f(x)=\begin{cases} \sqrt{x} & x>0.7 \\ x & x \leq 0.7 \end{cases}\)

함수의 결과로 얻어진 매트릭스를 “후광하니”라고 부르자. “원본하니”와 “후광하니”를 좌우로 나란히 배치하여 출력하라.

shiny_hani = np.sqrt(hani)*(hani>0.7)+hani*(hani<=0.7)
plt.imshow(np.concatenate([hani,shiny_hani],axis=1))

<matplotlib.image.AxesImage at 0x7f6a921677c0>

HW

없음