07wk-2: 이미지분석 (1)

이미지분석
Author

최규빈

Published

October 18, 2022

10/18: [이미지자료분석] CNN

CNN 예비학습, CNN 구현 with CPU, CNN 구현 with GPU, BCEWithLogisticLoss

  • toc:true
  • branch: master
  • badges: true
  • comments: true
  • author: 최규빈

강의영상

youtube: https://youtube.com/playlist?list=PLQqh36zP38-ymnoeGZPPvaaB35JmhRiTi

import

import torch 
import torchvision
from fastai.vision.all import * 
import time
import graphviz
def gv(s): return graphviz.Source('digraph G{ rankdir="LR"'+s + '; }');

data

- download data

path = untar_data(URLs.MNIST)

- training set

X0 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'training/0').ls()])
X1 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'training/1').ls()])
X = torch.concat([X0,X1])/255
y = torch.tensor([0.0]*len(X0) + [1.0]*len(X1)).reshape(-1,1)

- test set

X0 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'testing/0').ls()])
X1 = torch.stack([torchvision.io.read_image(str(fname)) for fname in (path/'testing/1').ls()])
XX = torch.concat([X0,X1])/255
yy = torch.tensor([0.0]*len(X0) + [1.0]*len(X1)).reshape(-1,1)
X.shape,XX.shape,y.shape,yy.shape
(torch.Size([12665, 1, 28, 28]),
 torch.Size([2115, 1, 28, 28]),
 torch.Size([12665, 1]),
 torch.Size([2115, 1]))

CNN 예비학습

기존의 MLP 모형

- 교재의 모형

gv('''
splines=line
subgraph cluster_1{
    style=filled;
    color=lightgrey;
    "x1"
    "x2"
    ".."
    "x784"
    label = "Layer 0"
}
subgraph cluster_2{
    style=filled;
    color=lightgrey;
    "x1" -> "node1"
    "x2" -> "node1"
    ".." -> "node1"
    
    "x784" -> "node1"
    "x1" -> "node2"
    "x2" -> "node2"
    ".." -> "node2"
    "x784" -> "node2"
    
    "x1" -> "..."
    "x2" -> "..."
    ".." -> "..."
    "x784" -> "..."

    "x1" -> "node30"
    "x2" -> "node30"
    ".." -> "node30"
    "x784" -> "node30"


    label = "Layer 1: ReLU"
}
subgraph cluster_3{
    style=filled;
    color=lightgrey;
    "node1" -> "y"
    "node2" -> "y"
    "..." -> "y"
    "node30" -> "y"
    label = "Layer 2: Sigmoid"
}
''')

- 왜 28 \(\times\) 28 이미지를 784개의 벡터로 만든 다음에 모형을 돌려야 하는가?

- 기존에 개발된 모형이 회귀분석 기반으로 되어있어서 결국 회귀분석 틀에 짜 맞추어서 이미지자료를 분석하는 느낌

- observation의 차원은 \(784\)가 아니라 \(1\times (28\times 28)\)이 되어야 맞다.

새로운 아키텍처의 제시

- 예전

\(\underset{(n,784)}{\bf X} \overset{l_1}{\to} \underset{(n,30)}{\boldsymbol u^{(1)}} \overset{relu}{\to} \underset{(n,30)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\boldsymbol u^{(2)}} \overset{sig}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}}=\underset{(n,1)}{\hat{\boldsymbol y}}\)

  • \(l_1\): 선형변환, feature를 뻥튀기하는 역할
  • \(relu\): 뻥튀기된 feature에 비선형을 추가하여 표현력 극대화
  • \(l_2\): 선형변환, 뻥튀기된 feature를 요약 하는 역할 (=데이터를 요약하는 역할)

- 새로운 아키텍처 - \(conv\): feature를 뻥튀기하는 역할 (2d ver \(l_1\) 느낌) - \(relu\): - \(pooling\): 데이터를 요약하는 역할

CONV 레이어 (선형변환의 2D 버전)

- 우선 연산하는 방법만 살펴보자.

(예시1)

torch.manual_seed(43052)
_conv = torch.nn.Conv2d(1,1,(2,2)) # 입력1, 출력1, (2,2) window size
_conv.weight.data, _conv.bias.data
(tensor([[[[-0.1733, -0.4235],
           [ 0.1802,  0.4668]]]]),
 tensor([0.2037]))
_X = torch.arange(0,4).reshape(1,2,2).float()
_X
tensor([[[0., 1.],
         [2., 3.]]])
(-0.1733)*0 + (-0.4235)*1 +\
(0.1802)*2 + (0.4668)*3 + 0.2037
1.541
_conv(_X)
tensor([[[1.5410]]], grad_fn=<SqueezeBackward1>)

(예시2) 잘하면 평균도 계산하겠다?

_conv.weight.data = torch.tensor([[[[1/4, 1/4],[1/4,1/4]]]])
_conv.bias.data = torch.tensor([0.0])
_conv(_X) , (0+1+2+3)/4
(tensor([[[1.5000]]], grad_fn=<SqueezeBackward1>), 1.5)

(예시3) 이동평균?

_X = torch.arange(0,25).float().reshape(1,5,5) 
_X
tensor([[[ 0.,  1.,  2.,  3.,  4.],
         [ 5.,  6.,  7.,  8.,  9.],
         [10., 11., 12., 13., 14.],
         [15., 16., 17., 18., 19.],
         [20., 21., 22., 23., 24.]]])
_conv(_X)
tensor([[[ 3.,  4.,  5.,  6.],
         [ 8.,  9., 10., 11.],
         [13., 14., 15., 16.],
         [18., 19., 20., 21.]]], grad_fn=<SqueezeBackward1>)

(예시4) window size가 증가한다면? (2d의 이동평균느낌)

_conv = torch.nn.Conv2d(1,1,(3,3)) # 입력1, 출력1, (3,3) window size
_conv.bias.data = torch.tensor([0.0])
_conv.weight.data = torch.tensor([[[[1/9,1/9,1/9],[1/9,1/9,1/9],[1/9,1/9,1/9]]]])
_X,_conv(_X)
(tensor([[[ 0.,  1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.,  9.],
          [10., 11., 12., 13., 14.],
          [15., 16., 17., 18., 19.],
          [20., 21., 22., 23., 24.]]]),
 tensor([[[ 6.0000,  7.0000,  8.0000],
          [11.0000, 12.0000, 13.0000],
          [16.0000, 17.0000, 18.0000]]], grad_fn=<SqueezeBackward1>))
(1+2+3+6+7+8+11+12+13)/9
7.0

(예시5) 피처뻥튀기

_X = torch.tensor([1.0,1.0,1.0,1.0]).reshape(1,2,2)
_X
tensor([[[1., 1.],
         [1., 1.]]])
_conv = torch.nn.Conv2d(1,8,(2,2))
_conv.weight.data.shape,_conv.bias.data.shape
(torch.Size([8, 1, 2, 2]), torch.Size([8]))
_conv(_X).reshape(-1)
tensor([-0.3464,  0.2739,  0.1069,  0.6105,  0.0432,  0.8390,  0.2353,  0.2345],
       grad_fn=<ReshapeAliasBackward0>)
torch.sum(_conv.weight.data[0,...])+_conv.bias.data[0],\
torch.sum(_conv.weight.data[1,...])+_conv.bias.data[1]
(tensor(-0.3464), tensor(0.2739))

결국 아래를 계산한다는 의미

torch.sum(_conv.weight.data,axis=(2,3)).reshape(-1)+ _conv.bias.data
tensor([-0.3464,  0.2739,  0.1069,  0.6105,  0.0432,  0.8390,  0.2353,  0.2345])
_conv(_X).reshape(-1)
tensor([-0.3464,  0.2739,  0.1069,  0.6105,  0.0432,  0.8390,  0.2353,  0.2345],
       grad_fn=<ReshapeAliasBackward0>)

(잔소리) axis 사용 익숙하지 않으면 아래 꼭 들으세요..

  • https://guebin.github.io/IP2022/2022/04/11/(6주차)-4월11일.html , numpy공부 4단계: 축

ReLU (2d)

_X = torch.randn(25).reshape(1,5,5)
_X
tensor([[[ 0.2656,  0.0780,  3.0465,  1.0151, -2.3908],
         [ 0.4749,  1.6519,  1.5454,  1.0376,  0.9291],
         [-0.7858,  0.4190,  2.6057, -0.4022,  0.2092],
         [ 0.9594,  0.6408, -0.0411, -1.0720, -2.0659],
         [-0.0996,  1.1351,  0.9758,  0.4952, -0.5475]]])
a1=torch.nn.ReLU()
a1(_X)
tensor([[[0.2656, 0.0780, 3.0465, 1.0151, 0.0000],
         [0.4749, 1.6519, 1.5454, 1.0376, 0.9291],
         [0.0000, 0.4190, 2.6057, 0.0000, 0.2092],
         [0.9594, 0.6408, 0.0000, 0.0000, 0.0000],
         [0.0000, 1.1351, 0.9758, 0.4952, 0.0000]]])

Maxpooling 레이어

_maxpooling = torch.nn.MaxPool2d((2,2))
_X = torch.arange(16).float().reshape(1,4,4) 
_X, _maxpooling(_X) 
(tensor([[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]),
 tensor([[[ 5.,  7.],
          [13., 15.]]]))
_X = torch.arange(25).float().reshape(1,5,5) 
_X, _maxpooling(_X) 
(tensor([[[ 0.,  1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.,  9.],
          [10., 11., 12., 13., 14.],
          [15., 16., 17., 18., 19.],
          [20., 21., 22., 23., 24.]]]),
 tensor([[[ 6.,  8.],
          [16., 18.]]]))
_X = torch.arange(36).float().reshape(1,6,6) 
_X, _maxpooling(_X) 
(tensor([[[ 0.,  1.,  2.,  3.,  4.,  5.],
          [ 6.,  7.,  8.,  9., 10., 11.],
          [12., 13., 14., 15., 16., 17.],
          [18., 19., 20., 21., 22., 23.],
          [24., 25., 26., 27., 28., 29.],
          [30., 31., 32., 33., 34., 35.]]]),
 tensor([[[ 7.,  9., 11.],
          [19., 21., 23.],
          [31., 33., 35.]]]))

CNN 구현 (CPU)

X.shape
torch.Size([12665, 1, 28, 28])

(1) Conv2d

c1 = torch.nn.Conv2d(1,16,(5,5))
print(X.shape)
print(c1(X).shape)
torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])

(2) ReLU

a1 = torch.nn.ReLU()
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])

(3) MaxPool2D

m1 =  torch.nn.MaxPool2d((2,2)) 
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)
torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])

(4) 적당히 마무리하고 시그모이드 태우자

- 펼치자.

(방법1)

m1(a1(c1(X))).reshape(-1,2304).shape
torch.Size([12665, 2304])
16*12*12 
2304

(방법2)

flttn = torch.nn.Flatten()
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)
print(flttn(m1(a1(c1(X)))).shape)
torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])
torch.Size([12665, 2304])

- 2304 \(\to\) 1 로 차원축소하는 선형레이어를 설계

l1 = torch.nn.Linear(in_features=2304,out_features=1) 
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)
print(flttn(m1(a1(c1(X)))).shape)
print(l1(flttn(m1(a1(c1(X))))).shape)
torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])
torch.Size([12665, 2304])
torch.Size([12665, 1])

- 시그모이드

a2 = torch.nn.Sigmoid()
l1 = torch.nn.Linear(in_features=2304,out_features=1) 
print(X.shape)
print(c1(X).shape)
print(a1(c1(X)).shape)
print(m1(a1(c1(X))).shape)
print(flttn(m1(a1(c1(X)))).shape)
print(l1(flttn(m1(a1(c1(X))))).shape)
print(a1(l1(flttn(m1(a1(c1(X)))))).shape)
torch.Size([12665, 1, 28, 28])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 24, 24])
torch.Size([12665, 16, 12, 12])
torch.Size([12665, 2304])
torch.Size([12665, 1])
torch.Size([12665, 1])

- 네트워크 설계

net = torch.nn.Sequential(
    c1, # 2d: 컨볼루션(선형변환), 피처 뻥튀기 
    a1, # 2d: 렐루(비선형변환)
    m1, # 2d: 맥스풀링: 데이터요약
    flttn, # 2d->1d 
    l1, # 1d: 선형변환
    a2 # 1d: 시그모이드(비선형변환) 
)
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters())
t1= time.time()
for epoc in range(100): 
    ## 1
    yhat = net(X) 
    ## 2
    loss = loss_fn(yhat,y) 
    ## 3
    loss.backward()
    ## 4
    optimizr.step()
    optimizr.zero_grad()
t2= time.time()
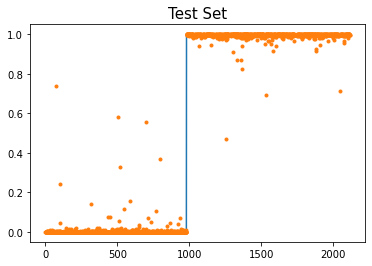
t2-t1
51.493837118148804
plt.plot(y)
plt.plot(net(X).data,'.')
plt.title('Traning Set',size=15)
Text(0.5, 1.0, 'Traning Set')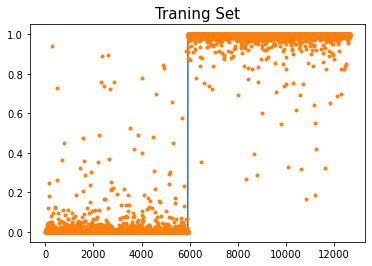

plt.plot(yy)
plt.plot(net(XX).data,'.')
plt.title('Test Set',size=15)
Text(0.5, 1.0, 'Test Set')

CNN 구현 (GPU)

1. dls

ds1=torch.utils.data.TensorDataset(X,y)
ds2=torch.utils.data.TensorDataset(XX,yy)
X.shape
torch.Size([12665, 1, 28, 28])
len(X)/10
1266.5
len(XX)
2115
dl1 = torch.utils.data.DataLoader(ds1,batch_size=1266) 
dl2 = torch.utils.data.DataLoader(ds2,batch_size=2115) 
dls = DataLoaders(dl1,dl2) # 이거 fastai 지원함수입니다

2. lrnr 생성: 아키텍처, 손실함수, 옵티마이저

net = torch.nn.Sequential(
    torch.nn.Conv2d(1,16,(5,5)),
    torch.nn.ReLU(),
    torch.nn.MaxPool2d((2,2)),
    torch.nn.Flatten(),
    torch.nn.Linear(2304,1),
    torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCELoss()
lrnr = Learner(dls,net,loss_fn)

3. 학습

lrnr.fit(10)
epoch train_loss valid_loss time
0 0.904232 0.605049 00:01
1 0.661176 0.371011 00:00
2 0.507179 0.213586 00:00
3 0.392649 0.113123 00:00
4 0.304377 0.065496 00:00
5 0.238253 0.043172 00:00
6 0.188984 0.031475 00:00
7 0.151837 0.024563 00:00
8 0.123364 0.020047 00:00
9 0.101180 0.016816 00:00

4. 예측 및 시각화

net.to("cpu") 
Sequential(
  (0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
  (1): ReLU()
  (2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
  (3): Flatten(start_dim=1, end_dim=-1)
  (4): Linear(in_features=2304, out_features=1, bias=True)
  (5): Sigmoid()
)

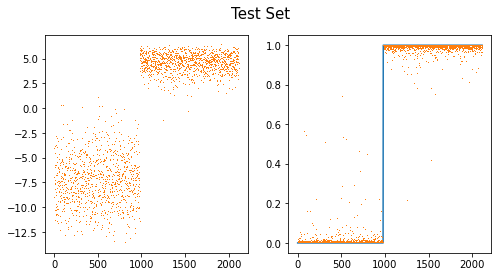
- 결과를 시각화하면 아래와 같다.

plt.plot(net(X).data,'.')
plt.title("Training Set",size=15)
Text(0.5, 1.0, 'Training Set')

plt.plot(net(XX).data,'.')
plt.title("Test Set",size=15)
Text(0.5, 1.0, 'Test Set')

- 빠르고 적합결과도 좋음

Lrnr 오브젝트

lrnr.model
Sequential(
  (0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
  (1): ReLU()
  (2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
  (3): Flatten(start_dim=1, end_dim=-1)
  (4): Linear(in_features=2304, out_features=1, bias=True)
  (5): Sigmoid()
)
net
Sequential(
  (0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
  (1): ReLU()
  (2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
  (3): Flatten(start_dim=1, end_dim=-1)
  (4): Linear(in_features=2304, out_features=1, bias=True)
  (5): Sigmoid()
)
id(lrnr.model), id(net)
(140681387850000, 140681387850000)
lrnr.model(X)
tensor([[5.4047e-03],
        [5.1475e-04],
        [9.8561e-04],
        ...,
        [9.9602e-01],
        [9.9584e-01],
        [9.9655e-01]], grad_fn=<SigmoidBackward0>)

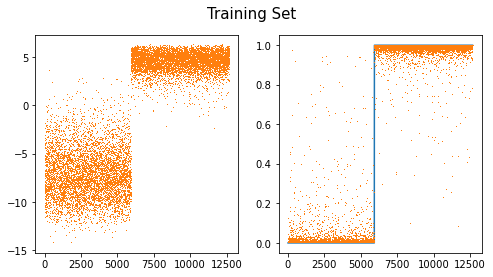
BCEWithLogitsLoss

- BCEWithLogitsLoss = Sigmoid + BCELoss - 왜 써요? 수치적으로 더 안정

- 사용방법

  1. dls 만들기
ds1=torch.utils.data.TensorDataset(X,y)
ds2=torch.utils.data.TensorDataset(XX,yy)
dl1 = torch.utils.data.DataLoader(ds1,batch_size=1266) 
dl2 = torch.utils.data.DataLoader(ds2,batch_size=2115) 
dls = DataLoaders(dl1,dl2) # 이거 fastai 지원함수입니다
  1. lrnr생성
net = torch.nn.Sequential(
    torch.nn.Conv2d(1,16,(5,5)),
    torch.nn.ReLU(),
    torch.nn.MaxPool2d((2,2)),
    torch.nn.Flatten(),
    torch.nn.Linear(2304,1),
    #torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCEWithLogitsLoss()
lrnr = Learner(dls,net,loss_fn)
  1. 학습
lrnr.fit(10)
epoch train_loss valid_loss time
0 0.896794 0.560268 00:00
1 0.613384 0.301413 00:00
2 0.454223 0.169741 00:00
3 0.346758 0.092166 00:00
4 0.268065 0.056573 00:00
5 0.210524 0.039757 00:00
6 0.167973 0.030431 00:00
7 0.135910 0.024560 00:00
8 0.111290 0.020503 00:00
9 0.092058 0.017516 00:00
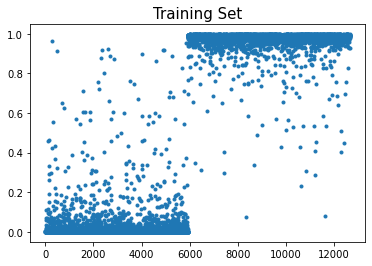
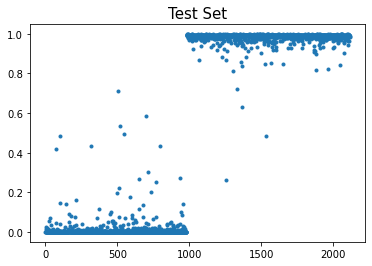
  1. 예측 및 시각화
net.to("cpu")
Sequential(
  (0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
  (1): ReLU()
  (2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), padding=0, dilation=1, ceil_mode=False)
  (3): Flatten(start_dim=1, end_dim=-1)
  (4): Linear(in_features=2304, out_features=1, bias=True)
)
fig,ax = plt.subplots(1,2,figsize=(8,4))
ax[0].plot(net(X).data,',',color="C1")
ax[1].plot(y)
ax[1].plot(a2(net(X)).data,',')
fig.suptitle("Training Set",size=15)
Text(0.5, 0.98, 'Training Set')

fig,ax = plt.subplots(1,2,figsize=(8,4))
ax[0].plot(net(XX).data,',',color="C1")
ax[1].plot(yy)
ax[1].plot(a2(net(XX)).data,',')
fig.suptitle("Test Set",size=15)
Text(0.5, 0.98, 'Test Set')