10wk-1: 순환신경망 (2)

순환신경망
Author

최규빈

Published

November 3, 2022

11/03: [순환신경망] 순환신경망 intro (2)

abc예제, abdc예제, AbAcAd예제(1)

강의영상

youtube: https://youtube.com/playlist?list=PLQqh36zP38-wXdABtimM1pYK5TjPTBA6X

import

import torch
import numpy as np
import matplotlib.pyplot as plt

Define some funtions

def f(txt,mapping):
    return [mapping[key] for key in txt] 
soft = torch.nn.Softmax(dim=1)

Exam2: abc

data

txt = list('abc')*100
txt[:10]
['a', 'b', 'c', 'a', 'b', 'c', 'a', 'b', 'c', 'a']
txt_x = txt[:-1]
txt_y = txt[1:]
txt_x[:5],txt_y[:5]
(['a', 'b', 'c', 'a', 'b'], ['b', 'c', 'a', 'b', 'c'])

하나의 은닉노드를 이용한 풀이 – 억지로 성공

- 데이터정리

mapping = {'a':0,'b':1,'c':2}
x = torch.tensor(f(txt_x,mapping))
y = torch.tensor(f(txt_y,mapping))
x[:5],y[:5]
(tensor([0, 1, 2, 0, 1]), tensor([1, 2, 0, 1, 2]))

- 학습

torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Embedding(num_embeddings=3,embedding_dim=1),
    torch.nn.Tanh(),
    #===#
    torch.nn.Linear(in_features=1,out_features=3)
)
loss_fn = torch.nn.CrossEntropyLoss()
optimizr = torch.optim.Adam(net.parameters())
for epoc in range(5000):
    ## 1
    ## 2 
    loss = loss_fn(net(x),y)
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

- 결과해석

hidden = net[:-1](x).data
yhat = soft(net(x)).data
plt.plot(hidden[:9],'--o')

plt.plot(net(x).data[:9],'--o')

plt.plot(yhat[:9],'--o')

  • 억지로 맞추고있긴한데 파라메터가 부족해보인다.

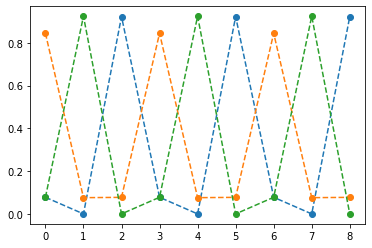
- 결과시각화1

fig,ax = plt.subplots(1,3,figsize=(15,5))
ax[0].plot(hidden[:9],'--o'); ax[0].set_title('$h:=(tanh \circ linr_1)(x)$',size=15)
ax[1].plot(net(x).data[:9],'--o'); ax[1].set_title('$net(x):=(linr_2 \circ tanh \circ linr_1)(x)$',size=15)
ax[2].plot(yhat[:9],'--o'); ax[2].set_title('$\hat{y}$ = softmax$(net(x))$',size=15);
fig.suptitle(r"Vis1: $h,net(x),\hat{y}$",size=20)
plt.tight_layout()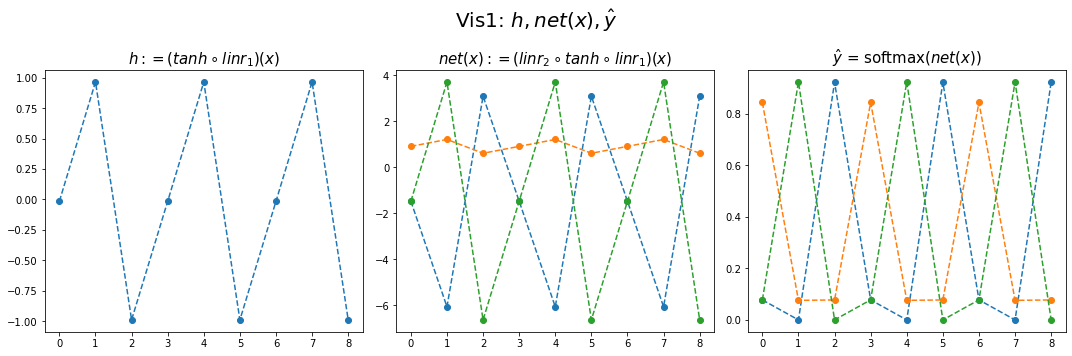

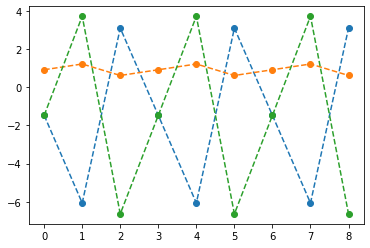
hidden[:9], (net[-1].weight.data).T, net[-1].bias.data
(tensor([[-0.0147],
         [ 0.9653],
         [-0.9896],
         [-0.0147],
         [ 0.9653],
         [-0.9896],
         [-0.0147],
         [ 0.9653],
         [-0.9896]]),
 tensor([[-4.6804,  0.3071,  5.2894]]),
 tensor([-1.5440,  0.9143, -1.3970]))
hidden[:9]@(net[-1].weight.data).T + net[-1].bias.data
tensor([[-1.4755,  0.9098, -1.4745],
        [-6.0618,  1.2108,  3.7086],
        [ 3.0875,  0.6104, -6.6312],
        [-1.4755,  0.9098, -1.4745],
        [-6.0618,  1.2108,  3.7086],
        [ 3.0875,  0.6104, -6.6312],
        [-1.4755,  0.9098, -1.4745],
        [-6.0618,  1.2108,  3.7086],
        [ 3.0875,  0.6104, -6.6312]])
  • (파랑,주황,초록) 순서로 그려짐
  • 파랑 = hidden * (-4.6804) + (-1.5440)
  • 주황 = hidden * (0.3071) + (0.9143)
  • 초록 = hidden * (5.2894) + (-1.3970)

- 내부동작을 잘 뜯어보니까 사실 엉성해. 엄청 위태위태하게 맞추고 있었음. - weight: 파랑과 초록을 구분하는 역할을 함 - weight + bias: 뭔가 교모하게 애매한 주황값을 만들어서 애매하게 ’b’라고 나올 확률을 학습시킨다. \(\to\) 사실 학습하는 것 같지 않고 때려 맞추는 느낌, 쓸수있는 weight가 한정적이라서 생기는 현상 (양수,음수,0)

참고: torch.nn.Linear()의 비밀? - 사실 \({\boldsymbol y}={\boldsymbol x}{\bf W} + {\boldsymbol b}\) 꼴에서의 \({\bf W}\)와 \({\boldsymbol b}\)가 저장되는게 아니다. - \({\boldsymbol y}={\boldsymbol x}{\bf A}^T + {\boldsymbol b}\) 꼴에서의 \({\bf A}\)와 \({\boldsymbol b}\)가 저장된다. - \({\bf W} = {\bf A}^T\) 인 관계에 있으므로 l1.weight 가 우리가 생각하는 \({\bf W}\) 로 해석하려면 사실 transpose를 취해줘야 한다.

왜 이렇게..? - 계산의 효율성 때문 (numpy의 구조를 알아야함) - \({\boldsymbol x}\), \({\boldsymbol y}\) 는 수학적으로는 col-vec 이지만 메모리에 저장할시에는 row-vec 로 해석하는 것이 자연스럽다. (사실 메모리는 격자모양으로 되어있지 않음)

잠깐 딴소리!!

(예시1)

_arr = np.array(range(4)).reshape(2,2)
_arr.strides
(16, 8)
  • 아래로 한칸 = 16칸 jump
  • 오른쪽으로 한칸 = 8칸 jump

(예시2)

_arr = np.array(range(6)).reshape(3,2)
_arr.strides
(16, 8)
  • 아래로 한칸 = 16칸 jump
  • 오른쪽으로 한칸 = 8칸 jump

(예시3)

_arr = np.array(range(6)).reshape(2,3)
_arr.strides
(24, 8)
  • 아래로 한칸 = 24칸 jump
  • 오른쪽으로 한칸 = 8칸 jump

(예시4)

_arr = np.array(range(4),dtype=np.int8).reshape(2,2)
_arr
array([[0, 1],
       [2, 3]], dtype=int8)
_arr.strides
(2, 1)
  • 아래로한칸 = 2칸 (= 2바이트 jump = 16비트 jump)
  • 오른쪽으로 한칸 = 1칸 jump (= 1바이트 jump = 8비트 jump)

진짜 참고..

  • 1바이트 = 8비트
  • 1바이트는 2^8=256 의 정보 표현
  • np.int8은 8비트로 정수를 저장한다는 의미
2**8
256
print(np.array(55,dtype=np.int8))
print(np.array(127,dtype=np.int8))
print(np.array(300,dtype=np.int8)) # overflow 
55
127
44

딴소리 끝!!

- 결과시각화2

combined  = torch.concat([hidden,net(x).data,yhat],axis=1)
combined.shape
torch.Size([299, 7])
fig,ax = plt.subplots(1,3,figsize=(15,5))
ax[0].plot(hidden[:9],'--o'); ax[0].set_title('$h:=(tanh \circ linr_1)(x)$',size=15)
ax[1].plot(net(x).data[:9],'--o'); ax[1].set_title('$net(x):=(linr_2 \circ tanh \circ linr_1)(x)$',size=15)
ax[2].plot(yhat[:9],'--o'); ax[2].set_title('$\hat{y}$ = softmax$(net(x))$',size=15);
fig.suptitle(r"Vis1: $h,net(x),\hat{y}$",size=20)
plt.tight_layout()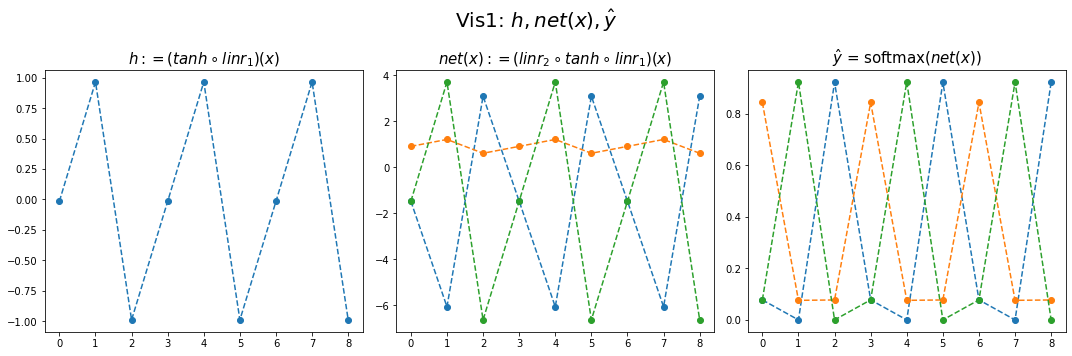

plt.matshow(combined[:15],vmin=-7,vmax=7,cmap='bwr')
plt.xticks(range(7), labels=[r'$h$',r'$y=a?$',r'$y=b?$',r'$y=c?$',r'$P(y=a)$',r'$P(y=b)$',r'$P(y=c)$'],size=14)
plt.colorbar()
plt.gcf().set_figwidth(15)
plt.gcf().set_figheight(15)
plt.title(r"Vis2: $[h | net(x) | \hat{y}]$",size=25)
Text(0.5, 1.0, 'Vis2: $[h | net(x) | \\hat{y}]$')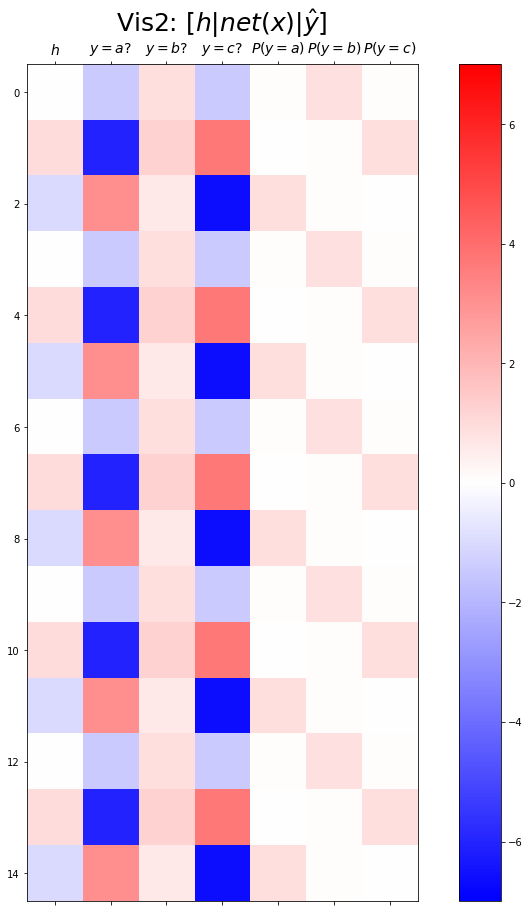

Exam3: abcd

data

txt = list('abcd')*100
txt[:10]
['a', 'b', 'c', 'd', 'a', 'b', 'c', 'd', 'a', 'b']
txt_x = txt[:-1]
txt_y = txt[1:]
txt_x[:5],txt_y[:5]
(['a', 'b', 'c', 'd', 'a'], ['b', 'c', 'd', 'a', 'b'])

하나의 은닉노드를 이용한 풀이 – 억지로 성공

- 데이터정리

mapping = {'a':0,'b':1,'c':2,'d':3}
x = torch.tensor(f(txt_x,mapping))
y = torch.tensor(f(txt_y,mapping))
x[:5],y[:5]
(tensor([0, 1, 2, 3, 0]), tensor([1, 2, 3, 0, 1]))

- 학습

net = torch.nn.Sequential(
    torch.nn.Embedding(num_embeddings=4,embedding_dim=1),
    torch.nn.Tanh(),
    torch.nn.Linear(in_features=1,out_features=4)
)
loss_fn = torch.nn.CrossEntropyLoss()
optimizr = torch.optim.Adam(net.parameters())
net[0].weight.data = torch.tensor([[-0.3333],[-2.5000],[5.0000],[0.3333]])

net[-1].weight.data = torch.tensor([[1.5000],[-6.0000],[-2.0000],[6.0000]])
net[-1].bias.data = torch.tensor([0.1500, -2.0000,  0.1500, -2.000])
for epoc in range(5000):
    ## 1
    ## 2 
    loss = loss_fn(net(x),y)
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

- 결과시각화1

hidden = net[:-1](x).data
yhat = soft(net(x)).data
fig,ax = plt.subplots(1,3,figsize=(15,5))
ax[0].plot(hidden[:9],'--o'); ax[0].set_title('$h:=(tanh \circ linr_1)(x)$',size=15)
ax[1].plot(net(x).data[:9],'--o'); ax[1].set_title('$net(x):=(linr_2 \circ tanh \circ linr_1)(x)$',size=15)
ax[2].plot(yhat[:9],'--o'); ax[2].set_title('$\hat{y}$ = softmax$(net(x))$',size=15);
fig.suptitle(r"Vis1: $h,net(x),\hat{y}$",size=20)
plt.tight_layout()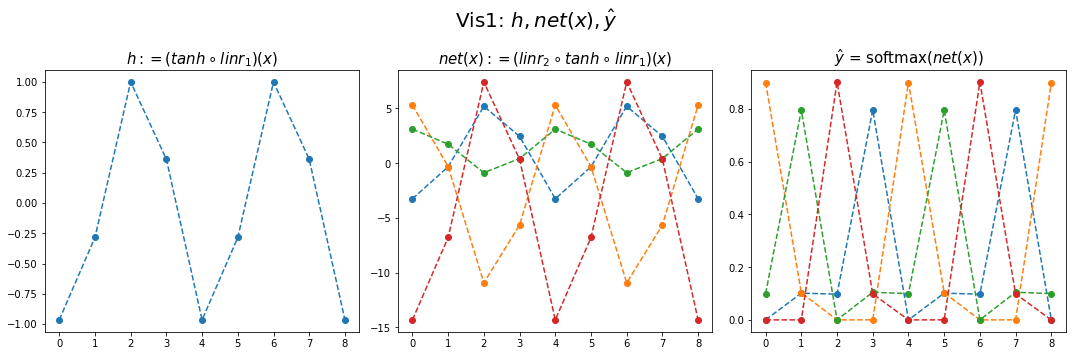

- 결과시각화2

combined  = torch.concat([hidden,net(x).data,yhat],axis=1)
combined.shape
torch.Size([399, 9])
plt.matshow(combined[:15],vmin=-15,vmax=15,cmap='bwr')
plt.xticks(range(9), labels=[r'$h$',r'$y=a?$',r'$y=b?$',r'$y=c?$',r'$y=d?$',r'$P(y=a)$',r'$P(y=b)$',r'$P(y=c)$',r'$P(y=d)$'],size=14)
plt.colorbar()
plt.gcf().set_figwidth(15)
plt.gcf().set_figheight(15)
plt.title(r"Vis2: $[h | net(x) | \hat{y}]$",size=25)
Text(0.5, 1.0, 'Vis2: $[h | net(x) | \\hat{y}]$')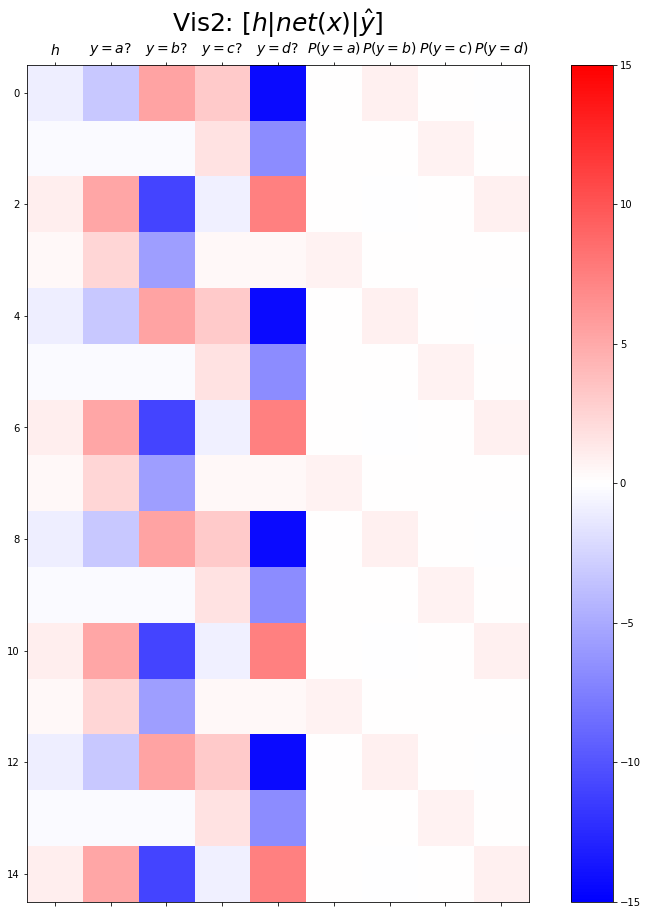

두개의 은닉노드를 이용한 풀이 – 깔끔한 성공

- 데이터정리

mapping = {'a':0,'b':1,'c':2,'d':3}
x = torch.tensor(f(txt_x,mapping))
y = torch.tensor(f(txt_y,mapping))
x[:5],y[:5]
(tensor([0, 1, 2, 3, 0]), tensor([1, 2, 3, 0, 1]))

- 학습

torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Embedding(num_embeddings=4,embedding_dim=2),
    torch.nn.Tanh(),
    torch.nn.Linear(in_features=2,out_features=4)
)
loss_fn = torch.nn.CrossEntropyLoss()
optimizr = torch.optim.Adam(net.parameters())
for epoc in range(5000):
    ## 1
    yhat = net(x)
    ## 2 
    loss = loss_fn(yhat,y)
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

- 결과시각화1

hidden = net[:-1](x).data
yhat = soft(net(x)).data
fig,ax = plt.subplots(1,3,figsize=(15,5))
ax[0].plot(hidden[:9],'--o'); ax[0].set_title('$h:=(tanh \circ linr_1)(x)$',size=15)
ax[1].plot(net(x).data[:9],'--o'); ax[1].set_title('$net(x):=(linr_2 \circ tanh \circ linr_1)(x)$',size=15)
ax[2].plot(yhat[:9],'--o'); ax[2].set_title('$\hat{y}$ = softmax$(net(x))$',size=15);
fig.suptitle(r"Vis1: $h,net(x),\hat{y}$",size=20)
plt.tight_layout()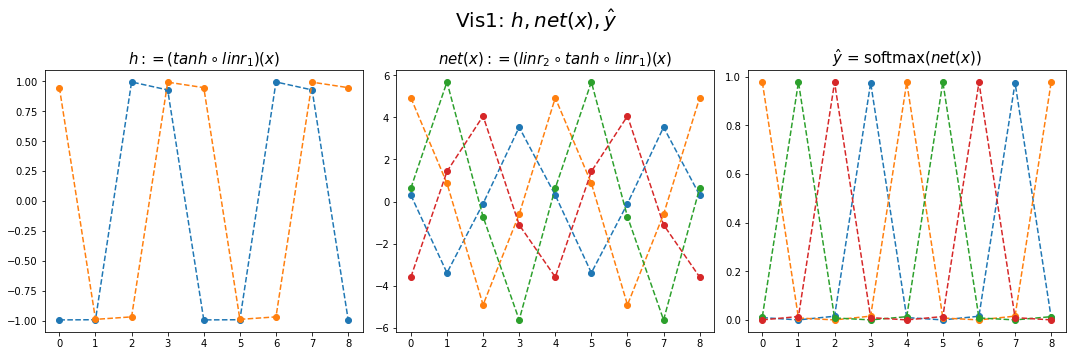

- 결과시각화2

combined  = torch.concat([hidden,net(x).data,yhat],axis=1)
combined.shape
torch.Size([399, 10])
plt.matshow(combined[:15],vmin=-7,vmax=7,cmap='bwr')
plt.xticks(range(10), labels=[r'$h$',r'$h$',r'$y=a?$',r'$y=b?$',r'$y=c?$',r'$y=d?$',r'$P(y=a)$',r'$P(y=b)$',r'$P(y=c)$',r'$P(y=d)$'],size=14)
plt.colorbar()
plt.gcf().set_figwidth(15)
plt.gcf().set_figheight(15)
plt.title(r"Vis2: $[h | net(x) | \hat{y}]$",size=25)
Text(0.5, 1.0, 'Vis2: $[h | net(x) | \\hat{y}]$')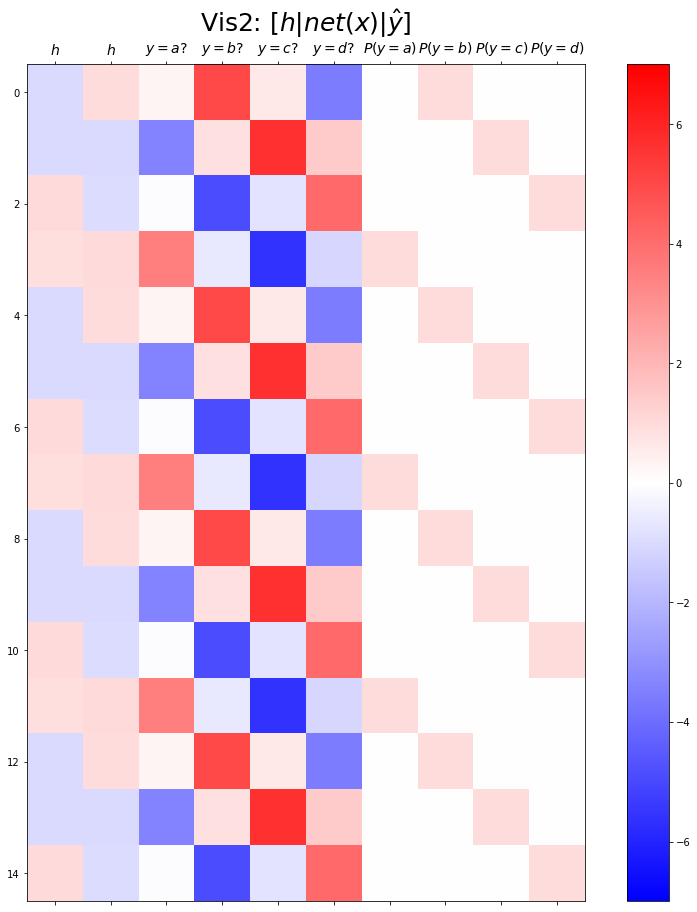

Exam4: AbAcAd

data

txt = list('AbAcAd')*100
txt[:10]
['A', 'b', 'A', 'c', 'A', 'd', 'A', 'b', 'A', 'c']
txt_x = txt[:-1]
txt_y = txt[1:]
txt_x[:5],txt_y[:5]
(['A', 'b', 'A', 'c', 'A'], ['b', 'A', 'c', 'A', 'd'])

두개의 은닉노드를 이용한 풀이 – 실패

- 데이터정리

mapping = {'A':0,'b':1,'c':2,'d':3}
x = torch.tensor(f(txt_x,mapping))
y = torch.tensor(f(txt_y,mapping))
x[:5],y[:5]
(tensor([0, 1, 0, 2, 0]), tensor([1, 0, 2, 0, 3]))

- 학습

torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Embedding(num_embeddings=4,embedding_dim=2),
    torch.nn.Tanh(),
    torch.nn.Linear(in_features=2,out_features=4)
)
loss_fn = torch.nn.CrossEntropyLoss()
optimizr = torch.optim.Adam(net.parameters())
for epoc in range(5000):
    ## 1
    yhat = net(x)
    ## 2 
    loss = loss_fn(yhat,y)
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

- 결과시각화1

hidden = net[:-1](x).data
yhat = soft(net(x)).data
fig,ax = plt.subplots(1,3,figsize=(15,5))
ax[0].plot(hidden[:9],'--o'); ax[0].set_title('$h:=(tanh \circ linr_1)(x)$',size=15)
ax[1].plot(net(x).data[:9],'--o'); ax[1].set_title('$net(x):=(linr_2 \circ tanh \circ linr_1)(x)$',size=15)
ax[2].plot(yhat[:9],'--o'); ax[2].set_title('$\hat{y}$ = softmax$(net(x))$',size=15);
fig.suptitle(r"Vis1: $h,net(x),\hat{y}$",size=20)
plt.tight_layout()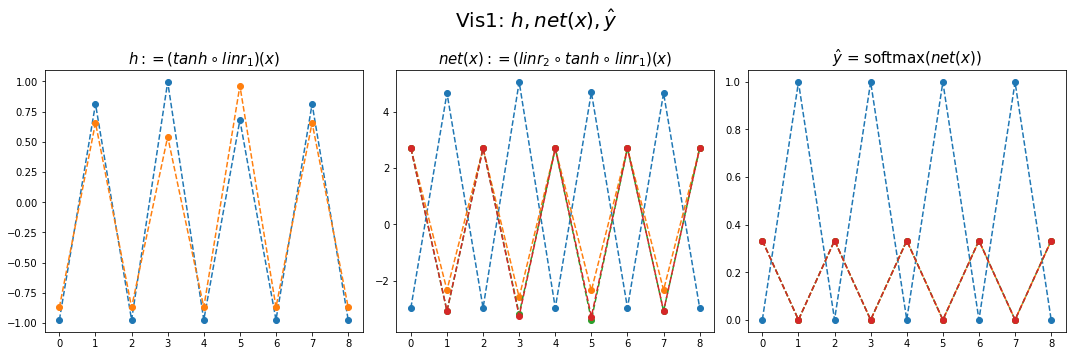

- 결과시각화2

combined  = torch.concat([hidden,net(x).data,yhat],axis=1)
combined.shape
torch.Size([599, 10])
plt.matshow(combined[:15],vmin=-5,vmax=5,cmap='bwr')
plt.xticks(range(10), labels=[r'$h$',r'$h$',r'$y=A?$',r'$y=b?$',r'$y=c?$',r'$y=d?$',r'$P(y=A)$',r'$P(y=b)$',r'$P(y=c)$',r'$P(y=d)$'],size=14)
plt.colorbar()
plt.gcf().set_figwidth(15)
plt.gcf().set_figheight(15)
plt.title(r"Vis2: $[h | net(x) | \hat{y}]$",size=25)
Text(0.5, 1.0, 'Vis2: $[h | net(x) | \\hat{y}]$')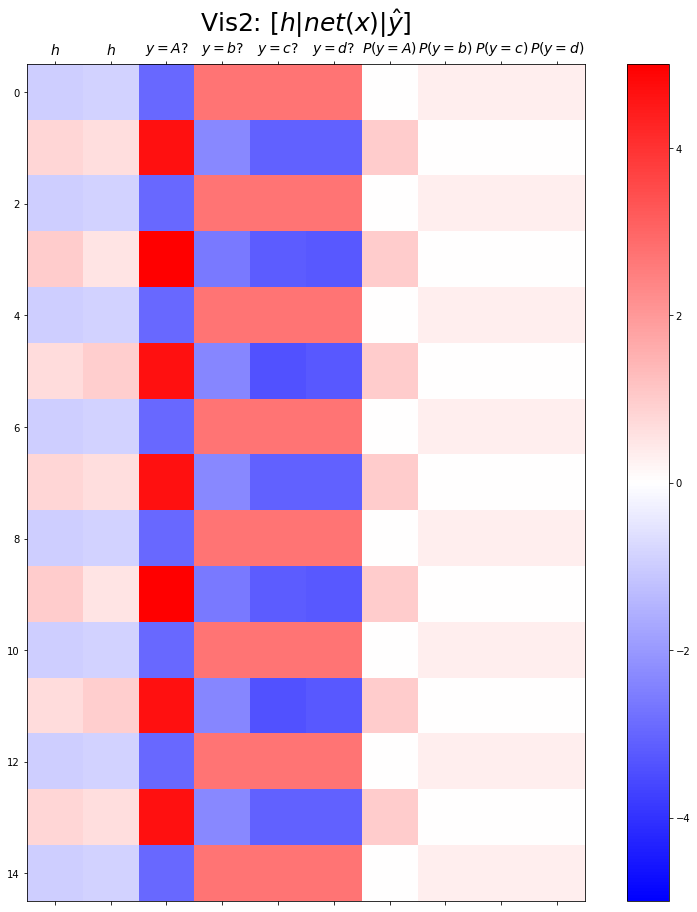

  • 실패

- 실패를 해결하는 순진한 접근방식: 위 문제를 해결하기 위해서는 아래와 같은 구조로 데이터를 다시 정리하면 될 것이다.

X y
A,b A
b,A c
A,c A
c,A d
A,d A
d,A b
A,b A
b,A c
… …

- 순진한 접근방식의 비판: - 결국 정확하게 직전 2개의 문자를 보고 다음 문제를 예측하는 구조 - 만약에 직전 3개의 문자를 봐야하는 상황이 된다면 또 다시 코드를 수정해야함. - 그리고 실전에서는 직전 몇개의 문자를 봐야하는지 모름.

이것에 대한 해결책은 순환신경망이다. 다음시간에 설명

숙제

주어진 자료가 다음과 같다고 하자.

txt = list('abcde')*100
txt[:10]
['a', 'b', 'c', 'd', 'e', 'a', 'b', 'c', 'd', 'e']
txt_x = txt[:-1]
txt_y = txt[1:]
txt_x[:5],txt_y[:5]
(['a', 'b', 'c', 'd', 'e'], ['b', 'c', 'd', 'e', 'a'])

아래 코드를 변형하여 적절한 네트워크를 설계하고 위의 자료를 학습하라. (깔끔한 성공을 위한 최소한의 은닉노드를 설정할 것)

net = torch.nn.Sequential(
    torch.nn.Embedding(num_embeddings=??,embedding_dim=??),
    torch.nn.Tanh(),
    torch.nn.Linear(in_features=??,out_features=??)
)

(풀이)

a,b,c,d,e 를 표현함에 있어서 3개의 은닉노드면 충분하다. - 1개의 은닉노드 -> 2개의 문자를 표현할 수 있음. - 2개의 은닉노드 -> 4개의 문자를 표현할 수 있음. - 3개의 은닉노드 -> 8개의 문자를 표현할 수 있음.

mapping = {'a':0,'b':1,'c':2,'d':3,'e':4}
x = torch.tensor(f(txt_x,mapping))
y = torch.tensor(f(txt_y,mapping))
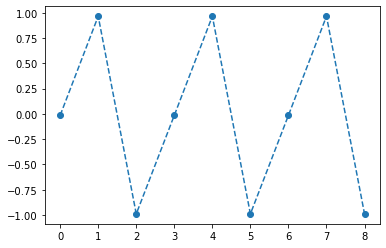
x[:5],y[:5]
(tensor([0, 1, 2, 3, 4]), tensor([1, 2, 3, 4, 0]))
torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Embedding(num_embeddings=5,embedding_dim=3),
    torch.nn.Tanh(),
    torch.nn.Linear(in_features=3,out_features=5)
)
loss_fn = torch.nn.CrossEntropyLoss()
optimizr = torch.optim.Adam(net.parameters())
for epoc in range(5000):
    ## 1
    yhat = net(x)
    ## 2 
    loss = loss_fn(yhat,y)
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

- 결과시각화1

hidden = net[:-1](x).data
yhat = soft(net(x)).data
fig,ax = plt.subplots(1,3,figsize=(15,5))
ax[0].plot(hidden[:9],'--o'); ax[0].set_title('$h:=(tanh \circ linr_1)(x)$',size=15)
ax[1].plot(net(x).data[:9],'--o'); ax[1].set_title('$net(x):=(linr_2 \circ tanh \circ linr_1)(x)$',size=15)
ax[2].plot(yhat[:9],'--o'); ax[2].set_title('$\hat{y}$ = softmax$(net(x))$',size=15);
fig.suptitle(r"Vis1: $h,net(x),\hat{y}$",size=20)
plt.tight_layout()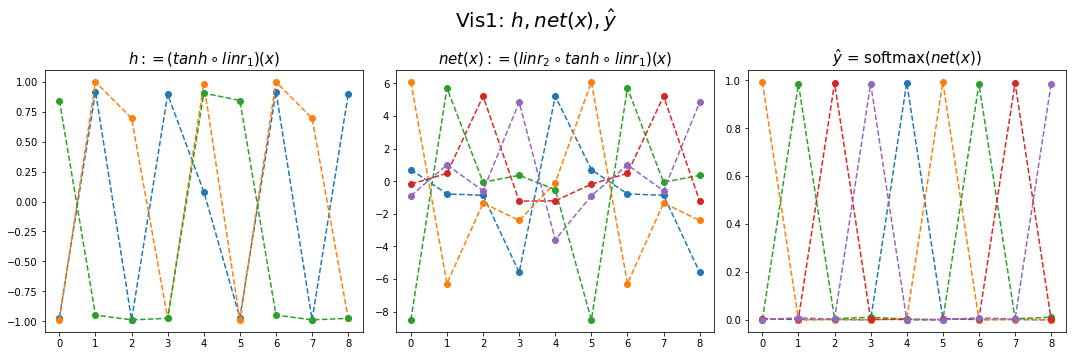

- 결과시각화2

combined  = torch.concat([hidden,net(x).data,yhat],axis=1)
combined.shape
torch.Size([499, 13])
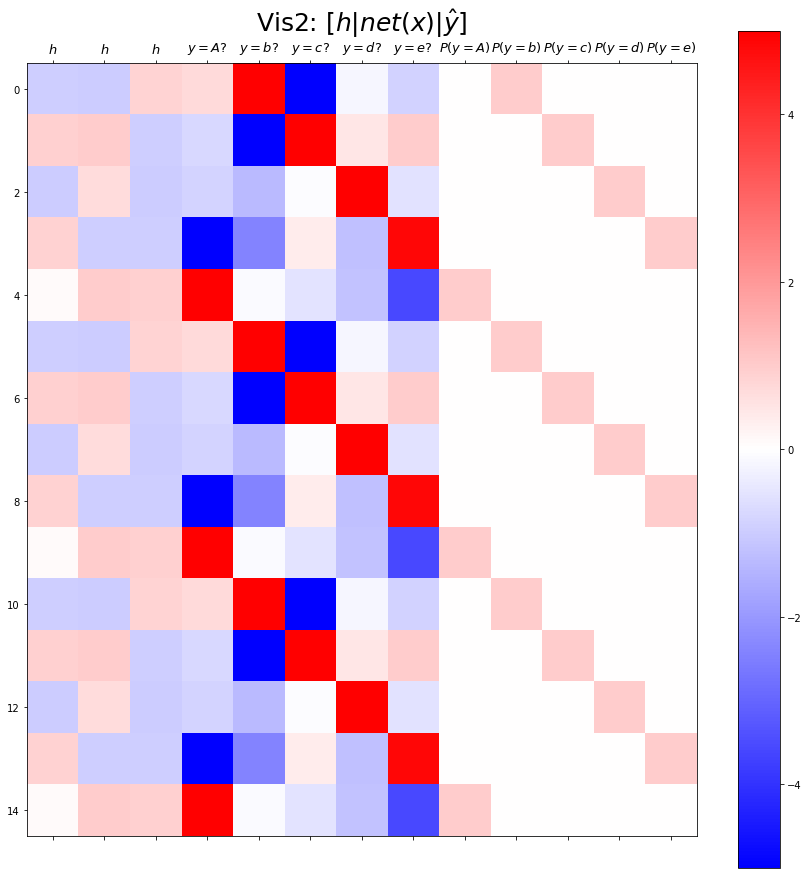
plt.matshow(combined[:15],vmin=-5,vmax=5,cmap='bwr')
plt.xticks(range(13), labels=[r'$h$',r'$h$',r'$h$',
                              r'$y=A?$',r'$y=b?$',r'$y=c?$',r'$y=d?$',r'$y=e?$',
                              r'$P(y=A)$',r'$P(y=b)$',r'$P(y=c)$',r'$P(y=d)$',r'$P(y=e)$'],size=13)
plt.colorbar()
plt.gcf().set_figwidth(15)
plt.gcf().set_figheight(15)
plt.title(r"Vis2: $[h | net(x) | \hat{y}]$",size=25)
Text(0.5, 1.0, 'Vis2: $[h | net(x) | \\hat{y}]$')