01wk-1: 박스플랏, 히스토그램

matplotlib
Author

최규빈

Published

September 4, 2023

박스플랏, 히스토그램

1. 강의영상

2. Import

import matplotlib.pyplot as plt 
import numpy as np 
#!pip install opencv-python
import cv2 
import matplotlib
matplotlib.rcParams['figure.figsize'] = (3, 2)  # 가로 6, 세로 4 크기의 그림
matplotlib.rcParams['figure.dpi'] = 150

3. Boxplot

A. motivating example

- 통계란?

- 평균 좋아해요?

# 예제1 – 전북고등학교: 평균은 좋은 측정값인가?

- 전북고등학교에서 통계학을 수업하는 A선생님과 B선생님의 있다.

y1=[75,75,76,76,77,77,78,79,79,98] # A선생님에게 통계학을 배운 학생의 점수들
y2=[76,76,77,77,78,78,79,80,80,81] # B선생님에게 통계학을 배운 학생의 점수들

- 어떤반이 더 공부를 잘할까?, 누가 더 잘 가르칠까?

np.mean(y1)
79.0
np.mean(y2)
78.2

- 의사결정: A선생님에게 배운 학생들의 평균이 더 높다. -> A선생님이 더 강의를 잘 하셨다?

- 반론: 평균은 A반(=A선생님에게 통계학을 배운 반)이 더 높다. 그런데 98점을 받은 학생이 A반에 포함되어서 A반이 전체평균이 높게 나온것이고 나머지 학생들은 전체적으로 B반 학생들이 더 시험을 잘 보았다고 해석할 수 있다.

- 교훈: 단순한 평균비교보다 학생들이 받은 점수의 분포를 비교해보는 것이 중요하다. 분포를 살펴보는 방법 중 유용한 방법이 박스플랏이다.

#

B. matplotlib으로 boxplot 그리기

- A반 학생들의 박스플랏 그리기

plt.boxplot(y1);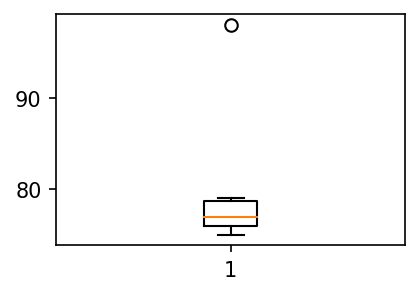

- B반 학생들의 박스플랏 그리기

plt.boxplot(y2);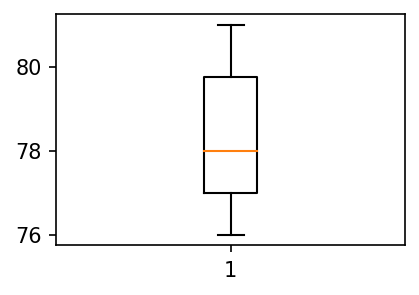

- A반 학생들의 점수와 B반 학생들의 점수를 나란히 박스플랏으로 그리자.

plt.boxplot([y1,y2]);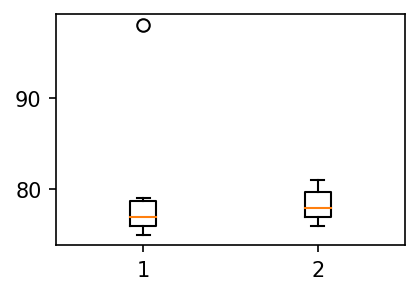

C. boxplot이란?

- Galarnyk (2023)

Galarnyk, Michael. 2023. “Python_tutorials.” https://github.com/mGalarnyk/Python_Tutorials.
Code 
np.random.seed(916170)

# connection path is here: https://stackoverflow.com/questions/6146290/plotting-a-line-over-several-graphs
mu, sigma = 0, 1 # mean and standard deviation
s = np.random.normal(mu, sigma, 1000)

fig, axes = plt.subplots(nrows = 1, ncols = 1, figsize=(10, 5))

# rectangular box plot
bplot = axes.boxplot(s,
                vert=False,
                patch_artist=True, 
                showfliers=True, # This would show outliers (the remaining .7% of the data)
                positions = [0],
                boxprops = dict(linestyle='--', linewidth=2, color='Black', facecolor = 'red', alpha = .4),
                medianprops = dict(linestyle='-', linewidth=2, color='Yellow'),
                whiskerprops = dict(linestyle='-', linewidth=2, color='Blue', alpha = .4),
                capprops = dict(linestyle='-', linewidth=2, color='Black'),
                flierprops = dict(marker='o', markerfacecolor='green', markersize=10,
                  linestyle='none', alpha = .4),
                widths = .3,
                zorder = 1)   

axes.set_xlim(-4, 4)
plt.xticks(fontsize = 14)

axes.set_yticks([])
axes.annotate(r'',
            xy=(-.73, .205), xycoords='data',
            xytext=(.66, .205), textcoords='data',
            arrowprops=dict(arrowstyle="|-|",
                            connectionstyle="arc3")
            );

axes.text(0, .25, "Interquartile Range \n(IQR)",  horizontalalignment='center', fontsize=18)
axes.text(0, -.21, r"Median", horizontalalignment='center', fontsize=16);
axes.text(2.65, -.15, "\"Maximum\"", horizontalalignment='center', fontsize=18);
axes.text(-2.65, -.15, "\"Minimum\"", horizontalalignment='center', fontsize=18);
axes.text(-.68, -.24, r"Q1", horizontalalignment='center', fontsize=18);
axes.text(-2.65, -.21, r"(Q1 - 1.5*IQR)", horizontalalignment='center', fontsize=16);
axes.text(.6745, -.24, r"Q3", horizontalalignment='center', fontsize=18);
axes.text(.6745, -.30, r"(75th Percentile)", horizontalalignment='center', fontsize=12);
axes.text(-.68, -.30, r"(25th Percentile)", horizontalalignment='center', fontsize=12);
axes.text(2.65, -.21, r"(Q3 + 1.5*IQR)", horizontalalignment='center', fontsize=16);

axes.annotate('Outliers', xy=(2.93,0.015), xytext=(2.52,0.20), fontsize = 18,
            arrowprops={'arrowstyle': '->', 'color': 'black', 'lw': 2},
            va='center');

axes.annotate('Outliers', xy=(-3.01,0.015), xytext=(-3.41,0.20), fontsize = 18,
            arrowprops={'arrowstyle': '->', 'color': 'black', 'lw': 2},
            va='center');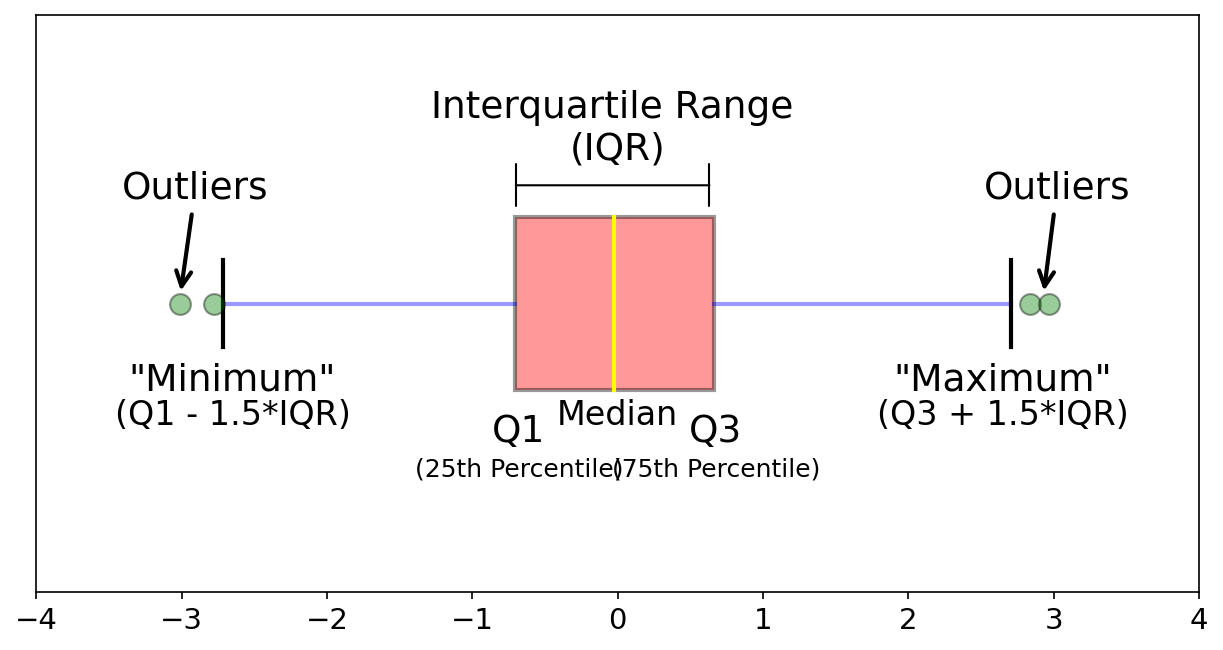

  • 가장 큰 값이 100%, 가장 작은 값이 0%, 중간값이 50%

D. boxplot을 언제 쓰면 좋을까?

- 박스플랏의 장점: 단순히 평균을 주는 것보다 데이터를 파악하고 직관을 얻기에 유리하다.

- 박스플랏이 이용되는 범위:

  • 첫 데이터 분석때 자료 분포를 파악하기 용이
  • Kaggel등의 대회참여시, 두 개 이상의 모형의 성능을 비교

4. Histogram

A. motivating example

- 전북고예제에서 우리의 소망: “A반 B반 중에 어떤 반이 공부를 더 잘하냐?”, “A선생님과 B선생님 중 어떤 분의 강의가 효과적이었다고 평할 수 있는가?” 와 같은 단순한 질문에 대한 대답

  • 보통 이러한 질문은 중심경향값 중 하나를 골라서 비교하면 되었다.
  • 여기에서 중심경향값이란 데이터 분포의 중심을 보여주는 값으로 자료 전체를 대표할 수 있는 값을 말함. 평균, 중앙값등이 대표적인 중심경향값이다.

- 전북고예제에서는 “A반 B반 중에서 어떤 반이 공부를 더 잘하냐?” 라는 질문의 대답으로 단순평균비교로는 의미가 없었다. 오히려 결과론적으로 보면 중앙값이 더 타당해 보인다.

- 그런데 사실 생각해보면 중앙값을 기준으로 B반이 공부를 더 잘했다고 주장하는 것도 애매하다. 어쨌든 가장 공부잘한 학생은 A반에 있으니까!

  • 에이 한명 뿐이잖아요? 라고 생각할 수 있는데 그 한명이 2명 3명으로 점점 늘어난다고 생각해보자, 합리적인 기준을 제시할 수 있는가?
  • 그리고 A반을 지도한 선생님이 영재를 지도하는데 특화된 선생님일수도 있잖아요?

- 사실 “A반 B반중에 누가 더 공부를 잘하냐?” 라는 질문은 굉장히 대답하기 곤란한 질문이다. 왜냐하면

  • 이슈1: 단순 평균비교로 이러한 질문에 답을 하기 어렵다.
  • 이슈2: 박스플랏으로 전체분포를 파악해도 어떠한 반이 더 공부를 잘한다는 기준을 잡는게 애매하다.

- 그런데 특수한 경우에는 “A반 B반중에 누가 더 공부를 잘하냐?” 라는 질문에 대한 대답을 깔끔하게 할 수 있다.

# 예제2 – 정규분포 전북고등학교: 평균은 좋은 측정값인가?

- A반과 B반의 통계학 성적이 아래와 같다고 하자.

np.random.seed(43052)
y1 = np.random.randn(10000)
y2 = np.random.randn(10000) + 0.5 
np.mean(y1),np.mean(y2)
(-0.011790879905079434, 0.4979147460611458)
np.mean(y2) - np.mean(y1)
0.5097056259662253

y2의 값이 y1의 값보다 전체적으로 0.5097056259662253 정도 높다고 볼 수 있다?

plt.boxplot([y1,y2]);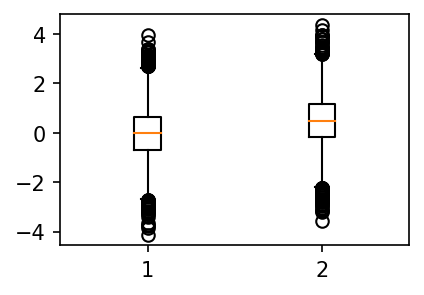

  • 분포의 모양이 거의 비슷, 왼쪽그림을 컨트롤+C 하여 오른쪽에 붙인다음 0.5정도 y축으로 올린느낌이다!

- 여기에서는 “B반의 성적 \(\approx\) A반의 성적 + 0.5” 라고 주장해도 큰 무리가 없어보인다. 따라서 이 경우에는 “A반 B반 중에 어떤반이 더 공부를 잘하냐?” 라는 질문에 대하여 “B반이 평균적으로 0.5점정도 더 공부를 잘합니다” 라고 대답해도 괜찮다.

  • 이 예제에서는 우연히 극단적인 학생이 없었음.
  • 그렇지만 혹시 극단적인 학생이 나온다면? 걱징X. 너무 극단적인 값이 많이 나오면 정규분포가 아님 + 만약에 어떠한 반에서 극단적인 학생이 나온다면 똑같은 확률로 다른반 역시 그러한 극단적 학생이 나올 것

- 결론: 정규분포 분포가정을 한다면 이슈1,2에 대한 문제를 한번에 해결가능 함

#

- 정규분포가정은 어떻게 할 수 있나? (= 데이터를 보고 어떻게 정규분포라고 알 수 있는가?): 데이터의 히스토그램을 그려서 종 모양이 되는지 확인해본다.1

  • 1 아직 초보단계라서 이것밖에 모를 수 있어요

    • B. histogram 이란?

    - 히스토그램: X축이 변수의 구간, Y축은 그 구간에 포함된 빈도를 의미하는 그림

    C. histogram 그리기

    - 히스토그램의 예시1 – 기본플랏, ;으로 결과 생략하기

    y=[10,11,12,15,16,20,21,22,23,24,25]
    plt.hist(y)
    (array([2., 1., 0., 1., 1., 0., 1., 1., 2., 2.]),
 array([10. , 11.5, 13. , 14.5, 16. , 17.5, 19. , 20.5, 22. , 23.5, 25. ]),
 <BarContainer object of 10 artists>)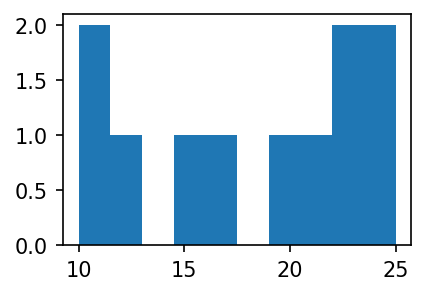

    plt.hist(y,bins=10)
    (array([2., 1., 0., 1., 1., 0., 1., 1., 2., 2.]),
 array([10. , 11.5, 13. , 14.5, 16. , 17.5, 19. , 20.5, 22. , 23.5, 25. ]),
 <BarContainer object of 10 artists>)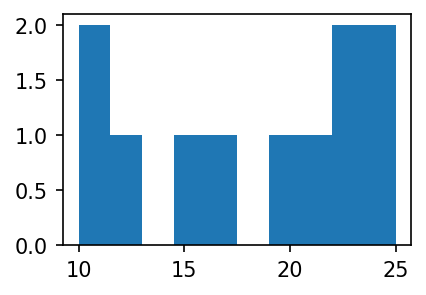

    - 히스토그램 예시2 – bins 옵션이용

    plt.hist(y,bins=3)
    (array([3., 2., 6.]),
 array([10., 15., 20., 25.]),
 <BarContainer object of 3 artists>)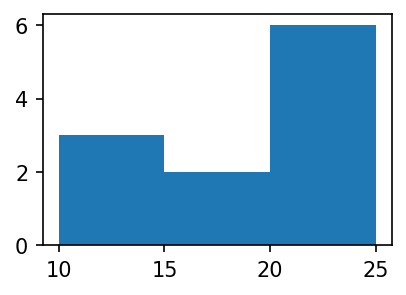

    - 히스토그램 예시3 – bins=3 옵션의 결과값 해석

    plt.hist(y,bins=3)
    (array([3., 2., 6.]),
 array([10., 15., 20., 25.]),
 <BarContainer object of 3 artists>)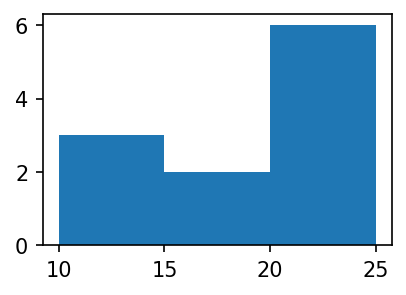

    • 가장 큰 값은 25, 가장 작은 값은 10이므로 range는 15이다.
    • range / bins = 15 / 3 = 5 이므로 각 구간의 간격은 5이다.
    • 구간은 [10,15), [15,20), [20,25] 로 나눈다.
    • 각 구간에 포함된 자료의 수는 3,2,6 이다.

    - 히스토그램 예시4 – bins=7 옵션의 결과값 해석

    plt.hist(y,bins=7) 
    (array([3., 0., 2., 0., 1., 2., 3.]),
 array([10.        , 12.14285714, 14.28571429, 16.42857143, 18.57142857,
        20.71428571, 22.85714286, 25.        ]),
 <BarContainer object of 7 artists>)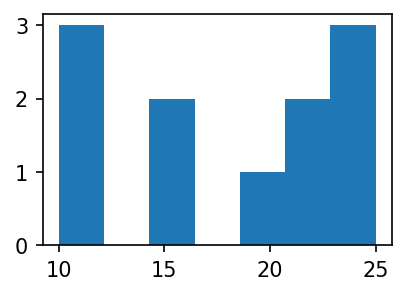

    • 가장 큰 값은 25, 가장 작은 값은 10이므로 range는 15이다.
    • range / bins = 15 / 7 = 2.142857142857143 이므로 각 구간의 간격은 2.142857142857143이다.
    • 구간은 [10,12.14285714), [12.14285714,14.28571429,), [22.85714286,25] 로 나눈다.
    • 각 구간에 포함된 자료의 수는 3,0,2,0,1,2,3 이다.

    - 히스토그램 예시5 – range 옵션

    plt.hist(y,bins=7,range=[0,30]) # range를 변경하면 --> 구간도 달라짐
    (array([0., 0., 3., 2., 2., 4., 0.]),
 array([ 0.        ,  4.28571429,  8.57142857, 12.85714286, 17.14285714,
        21.42857143, 25.71428571, 30.        ]),
 <BarContainer object of 7 artists>)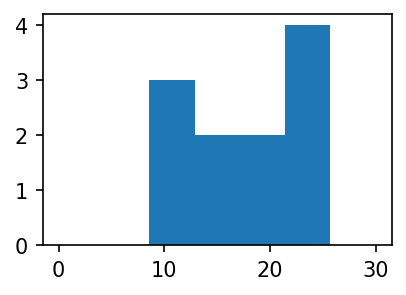

    - 히스토그램 예시6 – 나란히 그리기

    np.random.seed(43052)
y1 = np.random.randn(10000)
y2 = np.random.randn(10000) + 0.5 
plt.hist([y1,y2],bins=100);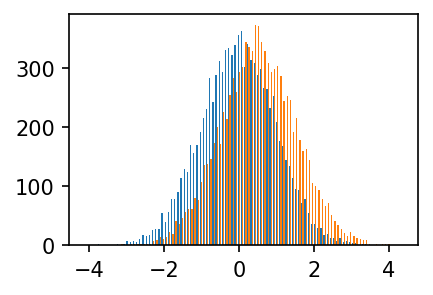

    5. Histogram equalization

    A. 예비학습1: 이미지자료 다운로드

    - ref: https://en.wikipedia.org/wiki/Histogram_equalization

    !wget https://upload.wikimedia.org/wikipedia/commons/0/08/Unequalized_Hawkes_Bay_NZ.jpg
img = cv2.imread('Unequalized_Hawkes_Bay_NZ.jpg')
!rm Unequalized_Hawkes_Bay_NZ.jpg
    --2023-09-04 11:59:07--  https://upload.wikimedia.org/wikipedia/commons/0/08/Unequalized_Hawkes_Bay_NZ.jpg
Resolving upload.wikimedia.org (upload.wikimedia.org)... 103.102.166.240, 2001:df2:e500:ed1a::2:b
Connecting to upload.wikimedia.org (upload.wikimedia.org)|103.102.166.240|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 110895 (108K) [image/jpeg]
Saving to: ‘Unequalized_Hawkes_Bay_NZ.jpg’

Unequalized_Hawkes_ 100%[===================>] 108.30K   572KB/s    in 0.2s    

2023-09-04 11:59:07 (572 KB/s) - ‘Unequalized_Hawkes_Bay_NZ.jpg’ saved [110895/110895]
    • !wget 주소: 주소에 있는 이미지를 다운로드
    • !rm 파일이름: 현재폴더에 “파일이름”을 삭제
    plt.imshow(img)

    • 다운받은 이미지를 보는 방법

    B. 예비학습2: 이미지자료의 이해

    비밀1: 이미지는 사실 숫자들의 집합이었음.

    - 예시1 – 2d array = 흑백이미지

    _img1 = np.array([0,30,90,120,150,180,210,240,255]).reshape(3,3)
_img1
    array([[  0,  30,  90],
       [120, 150, 180],
       [210, 240, 255]])
    plt.imshow(_img1,cmap='gray')
plt.colorbar()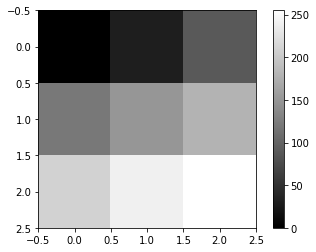

    - 예시2 – 2d array = 흑백이미지

    _img2 = np.array([0,20,40,60,80,100,120,140,160]).reshape(3,3)
_img2
    array([[  0,  20,  40],
       [ 60,  80, 100],
       [120, 140, 160]])
    plt.imshow(_img2,cmap='gray',vmin=0,vmax=255)
plt.colorbar()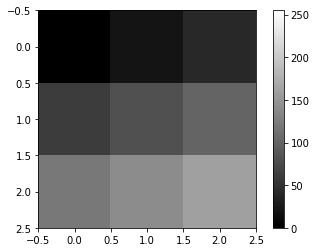

    - 예시3 – 나란히 그리기

    _img3 = np.concatenate([_img1,_img2],axis=1)
_img3
    array([[  0,  30,  90,   0,  20,  40],
       [120, 150, 180,  60,  80, 100],
       [210, 240, 255, 120, 140, 160]])
    plt.imshow(_img3,cmap='gray')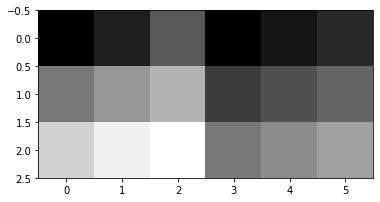

    비밀2: 칼라이미지는 red + green + blue 의 조합으로 표현가능 (다른방식도 가능)

    - ref: https://en.wikipedia.org/wiki/RGB_color_model

    그림 ??: 위키에서 긁은 그림, 빛의 3원색을 표현하고 있음

    - 예시1 – 3d array = 칼라이미지

    r = np.array(
    [[  0,   0,   0,   0,   0],
     [  0,   0,   0,   0,   0],
     [255, 255, 255, 255, 255],
     [255, 255, 255, 255, 255],
     [255, 255, 255, 255, 255]]
)
g = np.array(
    [[255, 255, 255,  0,   0],
     [255, 255, 255,  0,   0],
     [255, 255, 255,  0,   0],
     [  0,   0,   0,  0,   0],
     [  0,   0,   0,  0,   0]]
)
b = np.array(
    [[  0,   0, 255, 255, 255],
     [  0,   0, 255, 255, 255],
     [  0,   0, 255, 255, 255],
     [  0,   0,   0,   0,   0],
     [  0,   0,   0,   0,   0]]
)
z = np.array(
    [[ 0,  0,  0,  0,  0],
     [ 0,  0,  0,  0,  0],
     [ 0,  0,  0,  0,  0],
     [ 0,  0,  0,  0,  0],
     [ 0,  0,  0,  0,  0]]
)    
    red = np.stack([r,z,z],axis=-1)
green = np.stack([z,g,z],axis=-1)
blue = np.stack([z,z,b],axis=-1)
    plt.imshow(red)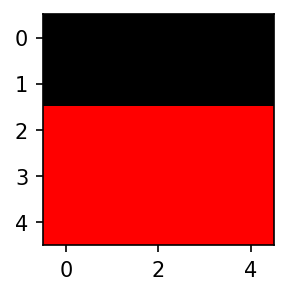

    plt.imshow(green)

    plt.imshow(blue)

    plt.imshow(red+green+blue)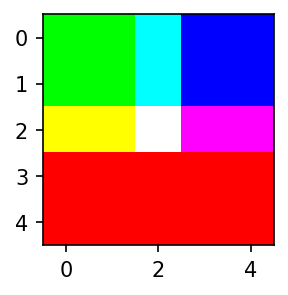

    - 예시2: R,G,B를 같은 비율로 섞으면 다시 흑백이미지가 된다.

    arr2 = np.array(
    [[10,  40],
     [80,  60]]
)
arr2
    array([[10, 40],
       [80, 60]])
    arr3 = np.stack([arr2,arr2,arr2],axis=-1)
plt.imshow(arr3)

    plt.imshow(arr2,cmap='gray',vmin=0,vmax=255)
plt.colorbar()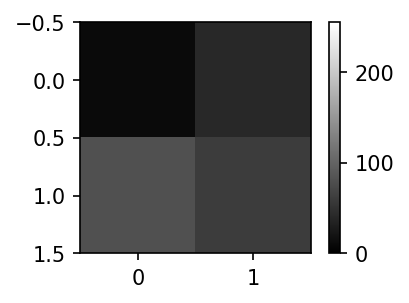

    C. 히스토그램 이퀄라이제이션

    - 우리가 관심있었던 이미지

    plt.imshow(img)

    - 이미지를 rgb로 각각 분리하고 각 색깔들의 히스토그램을 그려보자.

    r = img[:,:,0]
g = img[:,:,1]
b = img[:,:,2]
    plt.hist(r.reshape(-1),range=(0,255),bins=255);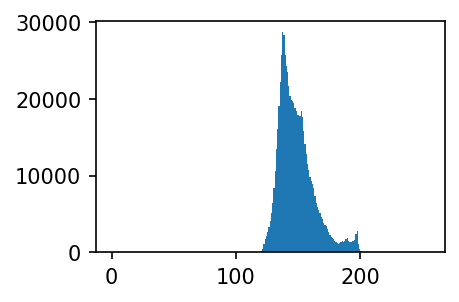

    • 120-200 사이에 값이 몰려있음
    • 만약에 120-200까지의 분포된 모양은 그대로 유지하면서 range를 0-255 까지 늘린다면?

    - cv2.equalizeHist()를 이용하여 분포의 모양은 대략적으로 유지하면서 값을 퍼트리자!

    rr = cv2.equalizeHist(r)
gg = cv2.equalizeHist(g)
bb = cv2.equalizeHist(b)
    plt.hist(r.reshape(-1),bins=255, range=[0,255],label='befor');
plt.hist(rr.reshape(-1),bins=255,range=[0,255],label='after');
plt.legend()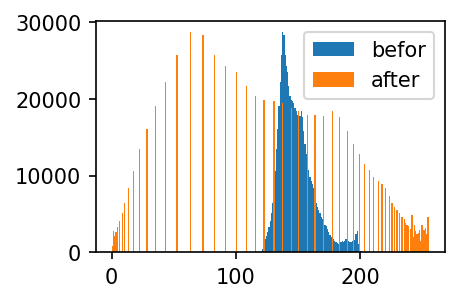

    - 변환이후의 이미지를 그려본다면?

    img2 = np.stack([rr,gg,bb],axis=-1)
    plt.imshow(img2)

    plt.imshow(np.concatenate([img,img2],axis=1))

    6. 참고

    - numpy에서 np.stack(), np.concatenate() 의 사용법을 복습하려면??

    - numpy, pandas, matplotlib에 대한 내용을 복습하려면?

    - 파이썬 전반적인 내용을 복습하려면?

    7. 숙제

    - HE(Histogram Equalization)을 이용하여 아래주소에 저장된 이미지의 명암비를 보정하라

    - 힌트: 아래는 위의 주소의 이미지를 다운로드 하여 img라는 numpy array로 저장한것 이다.

    !wget https://raw.githubusercontent.com/guebin/2021DV/master/_notebooks/hw_img.png
img = cv2.imread('hw_img.png')
!rm hw_img.png
    --2023-09-04 18:50:51--  https://raw.githubusercontent.com/guebin/2021DV/master/_notebooks/hw_img.png
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 185.199.109.133, 185.199.111.133, 185.199.108.133, ...
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|185.199.109.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 120618 (118K) [image/png]
Saving to: ‘hw_img.png’

hw_img.png          100%[===================>] 117.79K  --.-KB/s    in 0.01s   

2023-09-04 18:50:55 (10.8 MB/s) - ‘hw_img.png’ saved [120618/120618]

    - 아래는 다운로드한 이미지를 시각화한 결과이다.

    plt.imshow(img)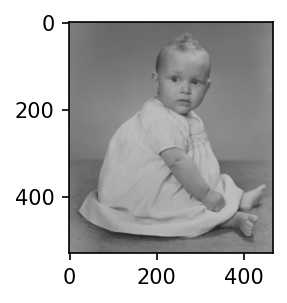

    숙제 관련 공지
    1. 숙제는 본인이 편리한 형식으로 정리하여 LMS에 제출
      • 화면캡쳐,.ipynb, .html 등 가능
    2. 숙제가 너무 어려워 못 하시는 분은 질문하시면 힌트 줍니다. (필요에 따라서 거의 정답에 가까운 힌트를 줄 수도 있습니다)
    파이썬을 처음 사용하는 학생을 위한 공지
    1. 기본적으로는 “파이썬프로그래밍 -> 데이터시각화” 순서로 수강하는 것을 권유합니다.
    2. 하지만 어떠한 이유로 “파이썬입문”없이 데이터시각화를 수강하셔야 하는 경우는 https://guebin.github.io/PP2023/ 에서 부족한 부분을 공부하시고 따라오시기 바랍니다. 중간고사 이전까지의 분량정도만 공부하면 충분합니다.
    3. 시간부족등의 이유로 https://guebin.github.io/PP2023/ 의 내용을 공부하기 어려우시다면, 질문을 아주 많이 하시면서 따라오셔야 합니다. (아무리 사소한거라도 다 답변합니다. 최대한 돕겠습니다.)