04wk-2: 깊은 신경망 (3) – 오버피팅, 드랍아웃, 신경망의 표현

Author

최규빈

Published

March 27, 2024

1. 강의영상

2. Imports

import torch
import matplotlib.pyplot as plt

3. 오버피팅 (시벤코정리의 이면)

A. 오버피팅

- 오버피팅이란?

위키: In mathematical modeling, overfitting is “the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably”.
제 개념: 데이터를 “데이터 = 언더라잉 + 오차”라고 생각할때 우리가 데이터로부터 적합할 것은 언더라잉인데 오차항을 적합하고 있는 현상.

B. 오버피팅 예시

- \(m\)이 매우 클때 아래의 네트워크 거의 무엇이든 맞출 수 있다고 보면 된다.

\(\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,m)}{\boldsymbol u^{(1)}} \overset{h}{\to} \underset{(n,m)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\hat{\boldsymbol y}}\)
\(\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,m)}{\boldsymbol u^{(1)}} \overset{sig}{\to} \underset{(n,m)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\hat{\boldsymbol y}}\)
\(\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,m)}{\boldsymbol u^{(1)}} \overset{relu}{\to} \underset{(n,m)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\hat{\boldsymbol y}}\)

- 그런데 종종 맞추지 말아야 할 것들도 맞춘다.

model: \(y_i = (0\times x_i) + \epsilon_i\), where \(\epsilon_i \sim N(0,0.01^2)\)

torch.manual_seed(5) 
x = torch.linspace(0,1,100).reshape(100,1)
y = torch.randn(100).reshape(100,1)*0.01
plt.plot(x,y,'--o',alpha=0.5)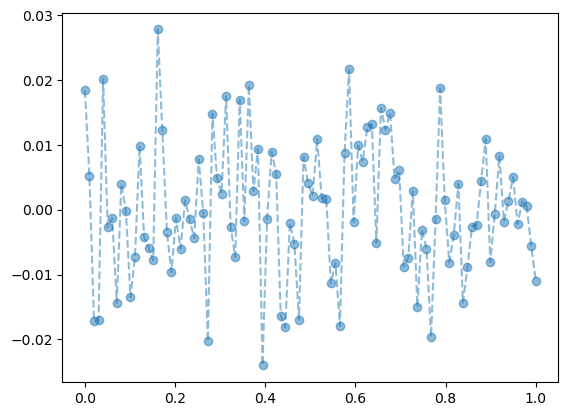

y는 그냥 정규분포에서 생성한 오차이므로 \(X \to y\) 로 향하는 규칙따위는 없음

torch.manual_seed(1) 
net=torch.nn.Sequential(
    torch.nn.Linear(in_features=1,out_features=512), 
    torch.nn.ReLU(),
    torch.nn.Linear(in_features=512,out_features=1)) 
optimizr= torch.optim.Adam(net.parameters())
loss_fn= torch.nn.MSELoss()

for epoc in range(1000): 
    ## 1 
    yhat=net(x) 
    ## 2 
    loss=loss_fn(yhat,y) 
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    net.zero_grad()

plt.plot(x,y,'--o',alpha=0.5)
plt.plot(x,net(x).data,'--')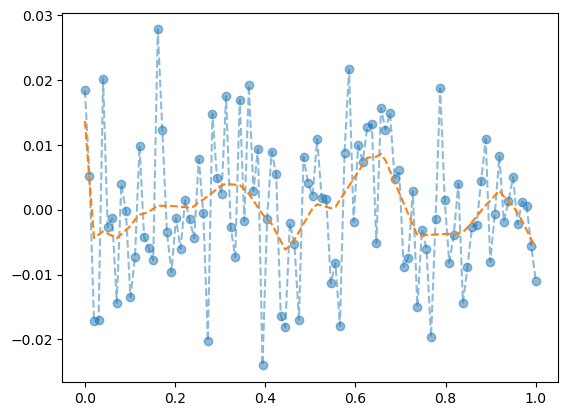

우리는 데이터를 랜덤에서 뽑았는데, 데이터의 추세를 따라간다 \(\to\) 오버피팅 (underlying이 아니라 오차항을 따라가고 있음)

C. 오버피팅이라는 뚜렷한 증거! (train / test)

- 데이터의 분리하여 보자.

torch.manual_seed(5) 
x_all = torch.linspace(0,1,100).reshape(100,1)
y_all = torch.randn(100).reshape(100,1)*0.01
x = x_all[:80] 
y = y_all[:80]
xx = x_all[80:]
yy = y_all[80:]
plt.plot(x,y,'--o',label="training (open)",alpha=0.7)
plt.plot(xx,yy,'--o',label="test (hidden)",alpha=0.3)
plt.legend()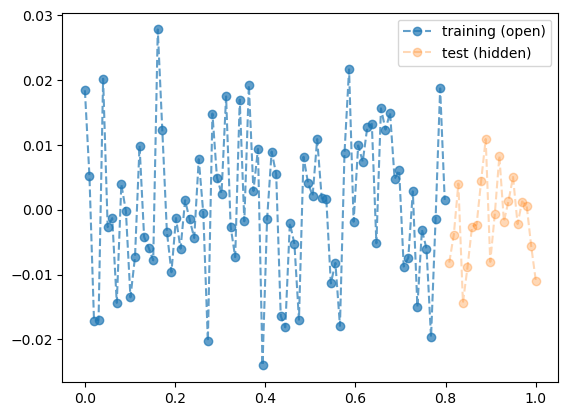

- train만 학습

torch.manual_seed(1) 
net=torch.nn.Sequential(
    torch.nn.Linear(in_features=1,out_features=512), 
    torch.nn.ReLU(),
    torch.nn.Linear(in_features=512,out_features=1)) 
optimizr= torch.optim.Adam(net.parameters())
loss_fn= torch.nn.MSELoss()

for epoc in range(1000): 
    ## 1 
    yhat = net(x) 
    ## 2 
    loss=loss_fn(yhat,y) 
    ## 3 
    loss.backward()
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

- training data로 학습한 net를 training data 에 적용

plt.plot(x,y,'--o',label="training data (open)",alpha=0.3)
plt.plot(xx,yy,'--o',label="test data (hidden)",alpha=0.3)
plt.plot(x,net(x).data,label="fitted values, predicted values",color="C0")
plt.legend()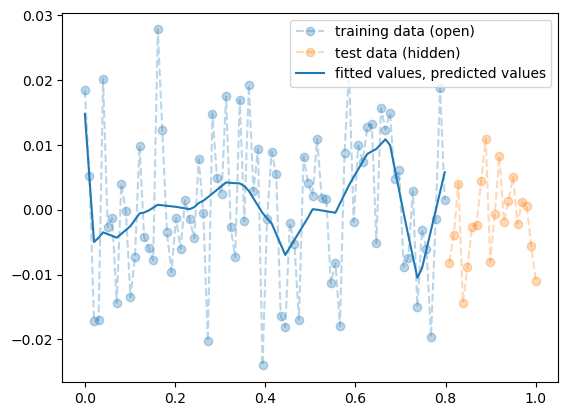

train에서는 잘 맞추는듯이 보인다.

- training data로 학습한 net를 test data 에 적용

plt.plot(x,y,'--o',label="training data (open)",alpha=0.3)
plt.plot(xx,yy,'--o',label="test data (hidden)",alpha=0.3)
plt.plot(x,net(x).data,label="fitted values, predicted values",color="C0")
plt.plot(xx,net(xx).data,label="predicted values, predicted values with new data",color="C1")
plt.legend()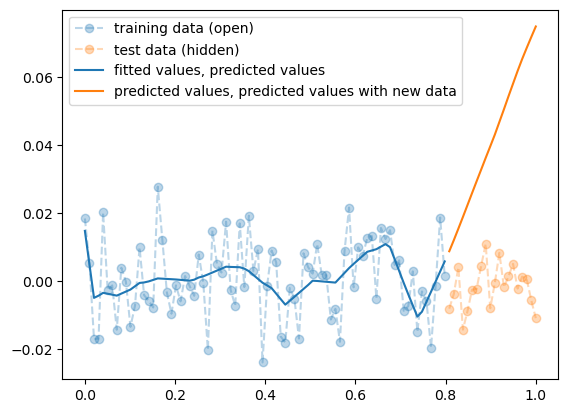

train은 그럭저럭 따라가지만 test에서는 엉망이다. \(\to\) overfit

D. 시벤코정리의 올바른 이해

시벤코정리의 항변(?) (Cybenko 1989)

하나의 은닉층을 가지는 아래와 같은 꼴의 네트워크 \(net: {\bf X}_{n \times p} \to {\bf y}_{n\times q}\)는

net = torch.nn.Sequential(
    torch.nn.Linear(p,???),
    torch.nn.Sigmoid(), ## <-- 여기에 렐루를 써도 된다. 
    torch.nn.Linear(???,q)
)

모든 continuous mapping

\[f: {\bf X}_{n \times p} \to {\bf y}_{n\times q}\]

를 원하는 정확도로 “근사”시킬 수 있다 (즉 마음만 먹으면 loss를 0에 가깝도록 만들 수 있다는 의다) 쉽게 말하면 \({\bf X} \to {\bf y}\) 인 어떠한 복잡한 규칙라도 하나의 은닉층을 가진 심층신경망(DNN)이 원하는 정확도로 근사시킨다는 의미이다. 그렇지만 이러한 규칙이 네크워크가 학습하지 못했던 자료 (처음 보는 자료, unseen data) \({\bf XX}_{m \times p}\), \({\bf yy}_{m \times p}\) 에 대하여서도 올바르게 적용된다라는 보장은 없다. 즉

\[{\bf X}_{n \times p} \to {\bf y}_{n\times q}\]

를 원하는 정확도로 근사시킨 네트워크라고 할지라도

\[{\bf XX}_{m \times p} \to {\bf yy}_{m\times q}\]

는 엉터리로 나올 수 있다. 시벤코는 넓은 신경망이 가지는 표현력의 한계를 수학적으로 밝혔을 뿐이다. 넓은 신경망이 우수한 신경망¹이라는 주장을 한적은 없다.

¹ 여기에서 우수하다는 말은 여러의미가 있어요, 오버피팅이 없는 신경망이라든가, 경제적인 신경망이라든가..

Cybenko, George. 1989. “Approximation by Superpositions of a Sigmoidal Function.” Mathematics of Control, Signals and Systems 2 (4): 303–14.

4. 드랍아웃

A. 오버피팅의 해결

- 오버피팅의 해결책: 드랍아웃

- 데이터 – 재활용

torch.manual_seed(5) 
x_all = torch.linspace(0,1,100).reshape(100,1)
y_all = torch.randn(100).reshape(100,1)*0.01
x = x_all[:80] 
y = y_all[:80]
xx = x_all[80:]
yy = y_all[80:]
plt.plot(x,y,'--o',label="training (open)",alpha=0.7)
plt.plot(xx,yy,'--o',label="test (hidden)",alpha=0.3)
plt.legend()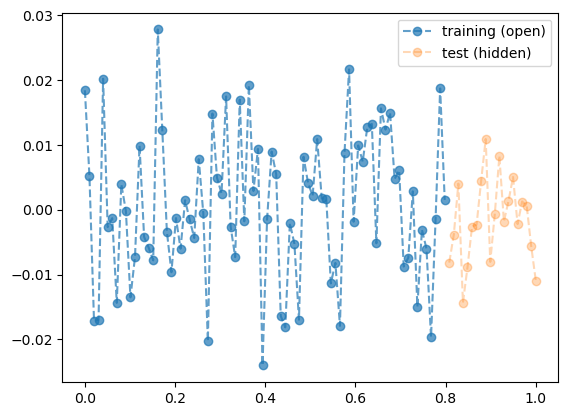

- 학습

torch.manual_seed(1) 
net = torch.nn.Sequential(
    torch.nn.Linear(in_features=1,out_features=512),
    torch.nn.ReLU(),
    torch.nn.Dropout(0.8),
    torch.nn.Linear(in_features=512,out_features=1)
)
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters())

for epoc in range(1000):
    ## 1 
    yhat = net(x)
    ## 2 
    loss = loss_fn(net(x),y) 
    ## 3 
    loss.backward() 
    ## 4 
    optimizr.step()
    optimizr.zero_grad()

- 결과시각화 (잘못된 사용)

plt.plot(x,y,'o')
plt.plot(xx,yy,'o')
plt.plot(x,net(x).data,'--',color='C0') 
plt.title(f"net.training = {net.training}",fontsize=15)

Text(0.5, 1.0, 'net.training = True')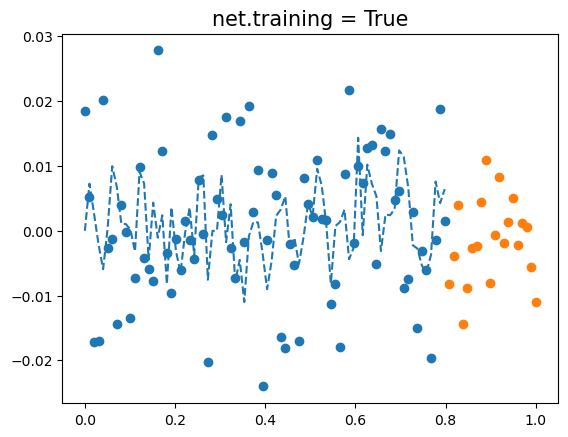

net에 드랍아웃이 포함되어 있다면, net.training == True 일때 결과가 엉망으로 나옴.
왜??

- 결과시각화 (올바른 사용)

net.training

True

net.eval()
net.training

False

plt.plot(x,y,'o')
plt.plot(xx,yy,'o')
plt.plot(x,net(x).data,'--',color='C0') 
plt.plot(xx,net(xx).data,'--',color='C1') 
plt.title(f"net.training = {net.training}",fontsize=15)

Text(0.5, 1.0, 'net.training = False')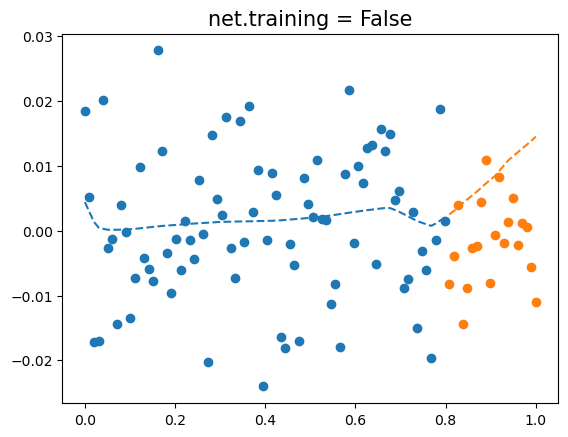

이게 제대로 된 결과시각화임!

B. 드랍아웃 레이어

u = torch.randn(20).reshape(10,2)
u

tensor([[ 1.2686, -0.8109],
        [-1.0100,  0.1346],
        [-1.9911, -0.9007],
        [ 0.7675, -0.7510],
        [ 2.1963, -0.4903],
        [-1.5218,  0.7236],
        [-0.4238,  0.0079],
        [ 1.5566,  1.6662],
        [ 1.4546,  0.2123],
        [-1.5117,  0.9293]])

d = torch.nn.Dropout(0.9)
d(u)

tensor([[12.6862, -0.0000],
        [-0.0000,  0.0000],
        [-0.0000, -0.0000],
        [ 0.0000, -0.0000],
        [ 0.0000, -0.0000],
        [-0.0000,  0.0000],
        [-0.0000,  0.0000],
        [ 0.0000,  0.0000],
        [ 0.0000,  0.0000],
        [-0.0000,  0.0000]])

90%의 드랍아웃: 드랍아웃층의 입력 중 임의로 90%를 골라서 결과를 0으로 만든다. + 그리고 0이 되지않고 살아남은 값들은 10배 만큼 값이 커진다.

- 드랍아웃레이어 정리

구조: 입력 -> 드랍아웃레이어 -> 출력
역할: (1) 입력의 일부를 임의로 0으로 만드는 역할 (2) 0이 안된것들은 스칼라배하여 드랍아웃을 통과한 모든 숫자들의 총합이 일정하게 되도록 조정
효과: 오버피팅을 억제하는 효과가 있음 (왜??) <– 이거 너무 시간이 없어서 대충 설명했는데요.. 잘 이해가 안되시면 2023-기계학습활용-11wk-43, 2023-기계학습활용-12wk-44 참고하시면 될 겁니다. 그래도 이해가 안되면 일단은 외우세요. (진짜 궁금하시면 따로 물어보세요.. 제가 이걸 설명할 시간이 없을것 같아요.. 죄송합니다)
의미: each iteration (each epoch x) 마다 학습에 참여하는 노드가 랜덤으로 결정됨.
느낌: 모든 노드가 골고루 학습가능 + 한 두개의 특화된 능력치가 개발되기 보다 평균적인 능력치가 전반적으로 개선됨

오버피팅을 잡는 방법은 드랍아웃만 있는게 아니다..

- ReLU + dropout의 특이한 성질

def my_dropout(x):
    x[:5,[0]] = torch.zeros(5).reshape(-1,1)
    x[5:,[1]] = torch.zeros(5).reshape(-1,1)
    return 2*x

relu = torch.nn.ReLU()
sig = torch.nn.Sigmoid()

relu(my_dropout(u)), my_dropout(relu(u))

(tensor([[0.0000, 0.0000],
         [0.0000, 0.2693],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [3.1132, 0.0000],
         [2.9091, 0.0000],
         [0.0000, 0.0000]]),
 tensor([[0.0000, 0.0000],
         [0.0000, 0.2693],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [0.0000, 0.0000],
         [3.1132, 0.0000],
         [2.9091, 0.0000],
         [0.0000, 0.0000]]))

sig(my_dropout(u)), my_dropout(sig(u))

(tensor([[0.5000, 0.1650],
         [0.5000, 0.5669],
         [0.5000, 0.1417],
         [0.5000, 0.1821],
         [0.5000, 0.2728],
         [0.0455, 0.5000],
         [0.2999, 0.5000],
         [0.9574, 0.5000],
         [0.9483, 0.5000],
         [0.0464, 0.5000]]),
 tensor([[0.0000, 0.6154],
         [0.0000, 1.0672],
         [0.0000, 0.5778],
         [0.0000, 0.6412],
         [0.0000, 0.7597],
         [0.3584, 0.0000],
         [0.7912, 0.0000],
         [1.6517, 0.0000],
         [1.6214, 0.0000],
         [0.3614, 0.0000]]))

드랍아웃은 히든레이어사이, 즉 활성화 함수 바로 뒤에 오는게 맞음. 그렇지만 ReLU의 경우 활성화 함수 직전에 취하기도 함.

5. 신경망의 표현 (\({\boldsymbol x} \to \hat{\boldsymbol y}\) 로 가는 과정을 그림으로 표현)

예제1: \(\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,1)}{\boldsymbol u^{(1)}} \overset{sig}{\to} \underset{(n,1)}{\boldsymbol v^{(1)}} =\underset{(n,1)}{\hat{\boldsymbol y}}\)

- 모든 observation과 가중치를 명시한 버전

(표현1)

단점: 똑같은 그림의 반복이 너무 많음

- observation 반복을 생략한 버전들

(표현2) 모든 \(i\)에 대하여 아래의 그림을 반복한다고 하면 (표현1)과 같다.

(표현3) 그런데 (표현2)에서 아래와 같이 \(x_i\), \(y_i\) 대신에 간단히 \(x\), \(y\)로 쓰는 경우도 많음

- 1을 생략한 버전들

(표현4) bais=False 대신에 bias=True를 주면 1을 생략할 수 있음

(표현4의 수정) \(\hat{w}_1\)대신에 \(\hat{w}\)를 쓰는 것이 더 자연스러움

(표현5) 선형변환의 결과는 아래와 같이 \(u\)로 표현하기도 한다.

다이어그램은 그리는 사람의 취향에 따라 그리는 방법이 조금씩 다릅니다. 즉 교재마다 달라요.

예제2: \(\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,2)}{\boldsymbol u^{(1)}} \overset{relu}{\to} \underset{(n,2)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\boldsymbol u^{(2)}} \overset{sig}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}} =\underset{(n,1)}{\hat{\boldsymbol y}}\)

참고: 코드로 표현

torch.nn.Sequential(
    torch.nn.Linear(in_features=1,out_features=2),
    torch.nn.ReLU(),
    torch.nn.Linear(in_features=2,out_features=1),
    torch.nn.Sigmoid()
)

- 이해를 위해서 03kw-2에서 다루었던 아래의 상황을 고려하자.

(강의노트의 표현)

(좀 더 일반화된 표현) 상황을 일반화하면 아래와 같다.

* Layer의 개념: \({\bf X}\)에서 \(\hat{\boldsymbol y}\)로 가는 과정은 “선형변환+비선형변환”이 반복되는 구조이다. “선형변환+비선형변환”을 하나의 세트로 보면 아래와 같이 표현할 수 있다.

\(\underset{(n,1)}{\bf X} \overset{l_1}{\to} \left( \underset{(n,2)}{\boldsymbol u^{(1)}} \overset{relu}{\to} \underset{(n,2)}{\boldsymbol v^{(1)}} \right) \overset{l_2}{\to} \left(\underset{(n,1)}{\boldsymbol u^{(2)}} \overset{sig}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}}\right), \quad \underset{(n,1)}{\boldsymbol v^{(2)}}=\underset{(n,1)}{net({\bf X})}=\underset{(n,1)}{\hat{\boldsymbol y}}\)

이것을 다이어그램으로 표현한다면 아래와 같다.

(선형+비선형을 하나의 Layer로 묶은 표현)

Layer를 세는 방법

제 방식: 학습가능한 파라메터가 몇층으로 있는지… <– 이것만 기억하세여
일부 교재 설명: 입력층은 계산하지 않음, activation layer는 계산하지 않음. <– 무시하세요.. 이러면 헷갈립니다..
위의 예제의 경우 number of layer = 2 이다.

Hidden Layer의 수를 세는 방법

제 방식: Hidden Layer의 수 = Layer의 수 -1 <– 이걸 기억하세여..
일부 교재 설명: Layer의 수 = Hidden Layer의 수 + 출력층의 수 = Hidden Layer의 수 + 1 <– 기억하지 마세여
위의 예제의 경우 number of hidden layer = 1 이다.

Important

무조건 학습가능한 파라메터가 몇겹으로 있는지만 판단하세요. 딴거 아무것도 생각하지마세여

## 예시1 -- 2층 (히든레이어는 1층)
torch.nn.Sequential(
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.ReLU(),
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
)

## 예시2 -- 2층 (히든레이어는 1층)
torch.nn.Sequential(
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.ReLU(),
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.Sigmoid(),
)

## 예시3 -- 1층 (히든레이어는 없음!!)
torch.nn.Sequential(
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
)

## 예시4 -- 1층 (히든레이어는 없음!!)
torch.nn.Sequential(
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.Sigmoid()
)

## 예시5 -- 3층 (히든레이어는 2층)
torch.nn.Sequential(
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.Sigmoid()
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.Sigmoid()
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층    
)

## 예시6 -- 3층 (히든레이어는 2층)
torch.nn.Sequential(
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.ReLU()
    torch.nn.Dropout(??)
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.ReLU()
    torch.nn.Dropout(??)
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층  
    torch.nn.Sigmoid()
)

Important

문헌에 따라서 레이어를 세는 개념이 제가 설명한 방식과 다른경우가 있습니다. 제가 설명한 방식보다 1씩 더해서 셉니다. 즉 아래의 경우 레이어를 3개로 카운트합니다.

## 예시1 -- 문헌에 따라 3층으로 세는 경우가 있음 (히든레이어는 1층)
torch.nn.Sequential(
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.ReLU(),
    torch.nn.Linear(??,??), ## <-- 학습해야할 가중치가 있는 층
    torch.nn.Sigmoid()
)

예를 들어 여기에서는 위의 경우 레이어는 3개라고 설명하고 있습니다. 이러한 카운팅은 “무시”하세요. 제가 설명한 방식이 맞아요. 이 링크 잘못(?) 나와있는 이유는 아래와 같습니다.

- 진짜 예전에 MLP를 소개할 초창기에서는 위의 경우 Layer를 3개로 셌음. (Rosenblatt et al. 1962)

- 그런데 요즘은 그렇게 안셈.. (그리고 애초에 MLP라는 용어도 잘 안쓰죠..)

참고로 히든레이어의 수는 예전방식이나 지금방식이나 동일하게 카운트하므로 히든레이어만 세면 혼돈이 없습니다.

Rosenblatt, Frank et al. 1962. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms. Vol. 55. Spartan books Washington, DC.

* node의 개념: \(u\to v\)로 가는 쌍을 간단히 노드라는 개념을 이용하여 나타낼 수 있음.

(노드의 개념이 포함된 그림)

여기에서 node의 숫자 = feature의 숫자와 같이 이해할 수 있다. 즉 아래와 같이 이해할 수 있다.

(“number of nodes = number of features”로 이해한 그림)

다이어그램의 표현방식은 교재마다 달라서 모든 예시를 달달 외울 필요는 없습니다. 다만 임의의 다이어그램을 보고 대응하는 네트워크를 pytorch로 구현하는 능력은 매우 중요합니다.

예제3: \(\underset{(n,784)}{\bf X} \overset{l_1}{\to} \underset{(n,32)}{\boldsymbol u^{(1)}} \overset{relu}{\to} \underset{(n,32)}{\boldsymbol v^{(1)}} \overset{l_1}{\to} \underset{(n,1)}{\boldsymbol u^{(2)}} \overset{sig}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}}=\underset{(n,1)}{\hat{\boldsymbol y}}\)

(다이어그램표현)

Layer0,1,2 대신에 Input Layer, Hidden Layer, Output Layer로 표현함

- 위의 다이어그램에 대응하는 코드

net = torch.nn.Sequential(
    torch.nn.Linear(in_features=28*28*1,out_features=32),
    torch.nn.ReLU(),
    torch.nn.Linear(in_features=32,out_features=1),
    torch.nn.Sigmoid() 
)

6. 숙제 – 나 혼자 내고 나 혼자 품..

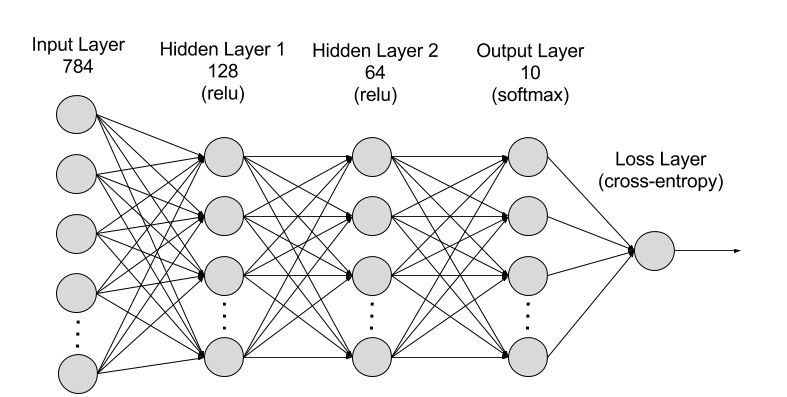
아래의 아키텍처를 가지는 네트워크를 파이토치코드로 선언하라.

출처: https://aws.amazon.com/ko/what-is/deep-learning/

net = torch.nn.Sequential(
    torch.nn.Linear(784,128),
    torch.nn.ReLU(),
    torch.nn.Linear(128,64),
    torch.nn.ReLU(),
    torch.nn.Linear(64,10),
    #torch.nn.Softmax()
)
loss_fn = torch.nn.CrossEntropyLoss() # <- 이 로스에 torch.nn.Softmax() 가 사실 포함되어있음..