회귀분석 (1) – 선형모형,손실함수,경사하강법
강의영상
https://youtube.com/playlist?list=PLQqh36zP38-xPdKoLnn2mMlwf9HLZTuib
imports
로드맵
- 회귀분석 \(\to\) 로지스틱 \(\to\) 심층신경망(DNN) \(\to\) 합성곱신경망(CNN)
- 강의계획서
ref
- 넘파이 문법이 약하다면? (reshape, concatenate, stack)
(1) reshape: 아래 링크의 넘파이공부 2단계 reshape 참고
https://guebin.github.io/IP2022/2022/04/06/(6주차)-4월6일.html
(2) concatenate, stack: 아래 링크의 넘파이공부 4단계 참고
회귀모형 소개
- model: \(y_i= w_0+w_1 x_i +\epsilon_i = 2.5 + 4x_i +\epsilon_i, \quad i=1,2,\dots,n\)
- model: \({\bf y}={\bf X}{\bf W} +\boldsymbol{\epsilon}\)
- \({\bf y}=\begin{bmatrix} y_1 \\ y_2 \\ \dots \\ y_n\end{bmatrix}, \quad {\bf X}=\begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \dots \\ 1 & x_n\end{bmatrix}, \quad {\bf W}=\begin{bmatrix} 2.5 \\ 4 \end{bmatrix}, \quad \boldsymbol{\epsilon}= \begin{bmatrix} \epsilon_1 \\ \dots \\ \epsilon_n\end{bmatrix}\)
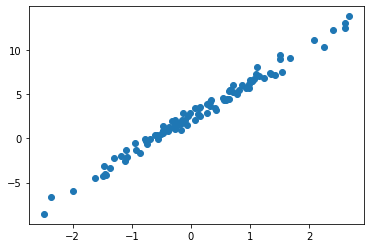
회귀모형에서 데이터 생성
회귀모형에서 학습이란?
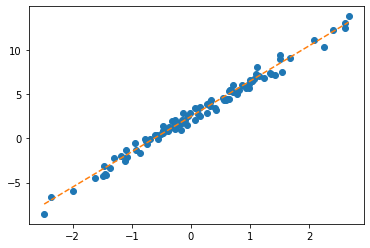
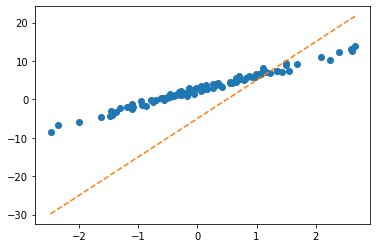
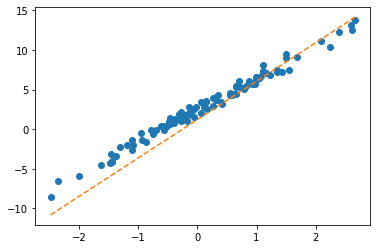
- 파란점만 주어졌을때, 주황색 점선을 추정하는것. 좀 더 정확하게 말하면 given data로 \(\begin{bmatrix} \hat{w}_0 \\ \hat{w}_1 \end{bmatrix}\)를 최대한 \(\begin{bmatrix} 2.5 \\ 4 \end{bmatrix}\)와 비슷하게 찾는것.
given data : \(\big\{(x_i,y_i) \big\}_{i=1}^{n}\)
parameter: \({\bf W}=\begin{bmatrix} w_0 \\ w_1 \end{bmatrix}\)
estimated parameter: \({\bf \hat{W}}=\begin{bmatrix} \hat{w}_0 \\ \hat{w}_1 \end{bmatrix}\)
- 더 쉽게 말하면 아래의 그림을 보고 적당한 추세선을 찾는것이다.
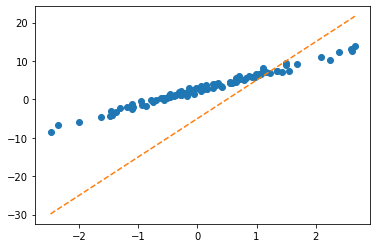
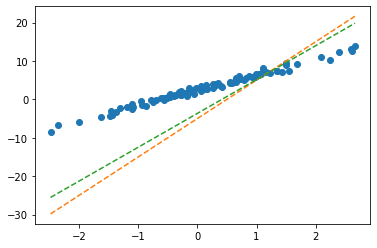
- 시도: \((\hat{w}_0,\hat{w}_1)=(-5,10)\)을 선택하여 선을 그려보고 적당한지 판단.
- \(\hat{y}_i=-5 +10 x_i\) 와 같이 \(y_i\)의 값을 적합시키겠다는 의미
- 벡터표현으로 주황색점선을 계산
파라메터를 학습하는 방법 (적당한 선으로 업데이트 하는 방법)
- 이론적으로 추론 <- 회귀분석시간에 배운것
- 컴퓨터의 반복계산을 이용하여 추론 (손실함수도입 + 경사하강법) <- 우리가 오늘 파이토치로 실습해볼 내용.
- 전략: 아래와 같은 3단계 전략을 취한다.
- stage1: 아무 점선이나 그어본다..
- stage2: stage1에서 그은 점선보다 더 좋은 점선으로 바꾼다.
- stage3: stage1 - 2 를 반복한다.
Stage1: 첫번째 점선 – 임의의 선을 일단 그어보자
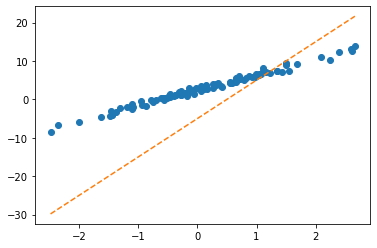
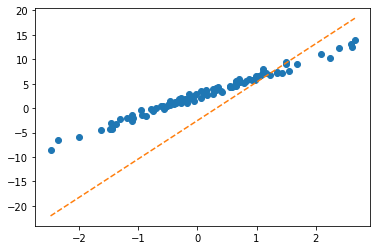
- \(\hat{w}_0=-5, \hat{w}_1 = 10\) 으로 설정하고 (왜? 그냥) 임의의 선을 그어보자.
처음에는 \({\bf \hat{W}}=\begin{bmatrix} \hat{w}_0 \\ \hat{w}_1 \end{bmatrix}=\begin{bmatrix} -5 \\ 10 \end{bmatrix}\) 를 대입해서 주황색 점선을 적당히 그려보자는 의미
끝에 requires_grad=True는 나중에 미분을 위한 것
그려보자!
Stage2: 첫번째 수정 – 최초의 점선에 대한 ‘적당한 정도’를 판단하고 더 ’적당한’ 점선으로 업데이트 한다.
- ’적당한 정도’를 판단하기 위한 장치: loss function 도입!
\(loss=\sum_{i=1}^{n}(y_i-\hat{y}_i)^2=\sum_{i=1}^{n}(y_i-(\hat{w}_0+\hat{w}_1x_i))^2\)
\(=({\bf y}-{\bf\hat{y}})^\top({\bf y}-{\bf\hat{y}})=({\bf y}-{\bf X}{\bf \hat{W}})^\top({\bf y}-{\bf X}{\bf \hat{W}})\)
- loss 함수의 특징 - \(y_i \approx \hat{y}_i\) 일수록 loss값이 작다. - \(y_i \approx \hat{y}_i\) 이 되도록 \((\hat{w}_0,\hat{w}_1)\)을 잘 찍으면 loss값이 작다. - (중요) 주황색 점선이 ‘적당할 수록’ loss값이 작다.
- 우리의 목표: 이 loss(=8587.6875)을 더 줄이자. - 궁극적으로는 아예 모든 조합 \((\hat{w}_0,\hat{w}_1)\)에 대하여 가장 작은 loss를 찾으면 좋겠다. (stage2에서 할일은 아님)
- 문제의 치환: 생각해보니까 우리의 문제는 아래와 같이 수학적으로 단순화 되었다. - 적당해보이는 주황색 선을 찾자 \(\to\) \(loss(w_0,w_1)\)를 최소로하는 \((w_0,w_1)\)의 값을 찾자.
- 수정된 목표: \(loss(w_0,w_1)\)를 최소로 하는 \((w_0,w_1)\)을 구하라. - 단순한 수학문제가 되었다. 마치 \(loss(w)=w^2-2w+3\) 을 최소화하는 \(w\)를 찾으라는 것과 같음. - 즉 “적당한 선으로 업데이트 하라 = 파라메터를 학습 하라 = 손실함수를 최소화 하라”
- 우리의 무기: 경사하강법, 벡터미분
Stage2를 위한 경사하강법 복습
경사하강법 아이디어 (1차원)
(step 1) 임의의 점을 찍는다.
(step 2) 그 점에서 순간기울기를 구한다. (접선) <– 미분
(step 3) 순간기울기(=미분계수)의 부호를 살펴보고 부호와 반대방향으로 움직인다.
(팁) 기울기의 절대값 크기와 비례하여 보폭(=움직이는 정도)을 조절한다.
경사하강법 아이디어 (2차원)
(step 1) 임의의 점을 찍는다.
(step 2) 그 점에서 순간기울기를 구한다. (접평면) <– 편미분
(step 3) 순간기울기(=미분계수)의 부호를 살펴보고 부호와 반대방향으로 각각 움직인다.
(팁) 기울기의 절대값 크기와 비례하여 보폭(=움직이는 정도)을 각각 조절한다.
loss를 줄이도록 \({\bf W}\)를 개선하는 방법
- \(\text{수정값} \leftarrow \text{원래값} - \text{기울어진크기}(=\text{미분계수}) \times \alpha\)
- 여기에서 \(\alpha\)는 전체적인 보폭의 크기를 결정한다. 즉 \(\alpha\)값이 클수록 한번의 update에 움직이는 양이 크다.
- \({\bf W} \leftarrow {\bf W} - \alpha \times \frac{\partial}{\partial {\bf W}}loss(w_0,w_1)\)
마이너스의 의미: 기울기의 부호를 보고 반대방향으로 움직여라.
\(\frac{\partial}{\partial {\bf W}}loss(w_0,w_1):\) 기울기의 절대값 크기와 비례하여 움직이는 정도를 조정하라.
\(\alpha\)의 의미: 전체적인 보폭의 속도를 조절, \(\alpha\)가 크면 전체적으로 빠르게 움직인다. 다리의 길이로 비유할 수 있다.
- 우리의 목표: loss=8587.6875 인데, 이걸 줄이는 것이 목표라고 했었음. 이것을 줄이는 방법이 경사하강법이다.
- 경사하강법으로 loss를 줄이기 위해서는 \(\frac{\partial}{\partial {\bf W}}loss(w_0,w_1)\)의 계산이 필요한데, 이를 위해서 벡터미분이 필요하다. (loss.backward()로 하면된다)
- loss.backward()의 의미: loss를 미분해라! 뭘로?
requires_grad=True를 가진 텐서로!!
loss=torch.sum((y-yhat)**2)= torch.sum((y-X@What)**2)
# 이었고
What=torch.tensor([-5.0,10.0],requires_grad=True)
# 이므로 결국 What으로 미분하라는 의미.
# 미분한 식이 나오는 것이 아니고,
# 그 식에 (-5.0, 10.0)을 대입한 계수값이 계산됨. - 위에서 loss.backward()의 과정은 미분을 활용하여 \((-5,10)\)에서의 순간기울기를 구했다는 의미임.
- (-5,10)에서 loss의 순간기울기 값은 What.grad로 확인가능하다.
- 이것이 의미하는건 \((-5,10)\)에서의 \(loss(w_0,w_1)\)의 순간기울기가 \((-1342.2523, 1188.9307)\) 이라는 의미
- (확인1) loss.backward()가 미분을 잘 계산해 주는 것이 맞는가? 손계산으로 검증하여 보자.
\(loss(w_0,w_1)=({\bf y}-\hat{\bf y})^\top ({\bf y}-\hat{\bf y})=({\bf y}-{\bf XW})^\top ({\bf y}-{\bf XW})\)
\(\frac{\partial}{\partial {\bf W} }loss(w_0,w_1)=-2{\bf X}^\top {\bf y}+2{\bf X}^\top {\bf X W}\)
- (확인2) loss.backward()가 미분을 잘 계산해 주는 것이 맞는가? 편미분을 간단히 구현하여 검증하여 보자.
\(\frac{\partial}{\partial {\bf W} } loss(w_0,w_1)=\begin{bmatrix}\frac{\partial}{\partial w_0} \\ \frac{\partial}{\partial w_1} \end{bmatrix}loss(w_0,w_1) =\begin{bmatrix}\frac{\partial}{\partial w_0}loss(w_0,w_1) \\ \frac{\partial}{\partial w_1}loss(w_0,w_1) \end{bmatrix}\)
\(\frac{\partial}{\partial w_0}loss(w_0,w_1) \approx \frac{loss(w_0+h,w_1)-loss(w_0,w_1)}{h}\)
\(\frac{\partial}{\partial w_1}loss(w_0,w_1) \approx \frac{loss(w_0,w_1+h)-loss(w_0,w_1)}{h}\)
(tensor(-1341.7968), tensor(1190.4297))- 약간 오차가 있지만 얼추비슷 \(\to\) 잘 계산했다는 소리임
- 수정전, 수정하는폭, 수정후의 값은 차례로 아래와 같다.
alpha=0.001
print('수정전: ' + str(What.data)) # What 에서 미분꼬리표를 떼고 싶다면? What.data or What.detach()
print('수정하는폭: ' +str(-alpha * What.grad))
print('수정후: ' +str(What.data-alpha * What.grad))
print('*참값: (2.5,4)' )수정전: tensor([-5., 10.])
수정하는폭: tensor([ 1.3423, -1.1889])
수정후: tensor([-3.6577, 8.8111])
*참값: (2.5,4)- Wbefore, Wafter 계산
(tensor([-5., 10.]), tensor([-3.6577, 8.8111]))- Wbefore, Wafter의 시각화
Stage3: Learn (=estimate \(\bf\hat{W})\)
- 이 과정은 Stage1,2를 반복하면 된다.
- 원래 철자는 epoch이 맞아요
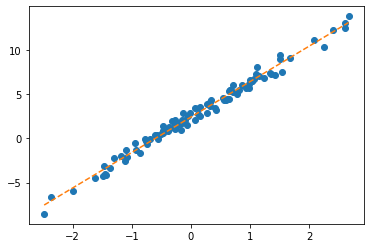
- 반복결과는?! (최종적으로 구해지는 What의 값은?!) - 참고로 true
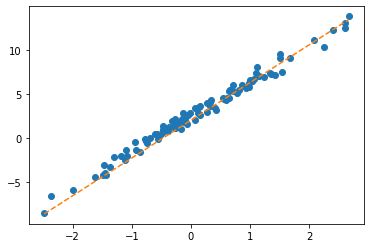
- 반복결과를 시각화하면?
파라메터의 학습과정 음미 (학습과정 모니터링)
학습과정의 기록
- 기록을 해보자.
What= torch.tensor([-5.0,10.0],requires_grad=True)
alpha=0.001
for epoc in range(30):
yhat=X@What ; yhat_history.append(yhat.data.tolist())
loss=torch.sum((y-yhat)**2); loss_history.append(loss.item())
loss.backward()
What.data = What.data-alpha * What.grad; What_history.append(What.data.tolist())
What.grad=None- \(\hat{y}\) 관찰 (epoch=3, epoch=10, epoch=15)
- \(\hat{\bf W}\) 관찰
[[-3.657747745513916, 8.81106948852539],
[-2.554811716079712, 7.861191749572754],
[-1.649186372756958, 7.101552963256836],
[-0.9060714244842529, 6.49347448348999],
[-0.29667872190475464, 6.006272315979004],
[0.2027742564678192, 5.615575313568115],
[0.6119104623794556, 5.302003860473633],
[0.9469034075737, 5.0501298904418945],
[1.2210698127746582, 4.847658157348633],
[1.4453644752502441, 4.684779644012451],
[1.6287914514541626, 4.553659915924072],
[1.7787461280822754, 4.448036193847656],
[1.9012980461120605, 4.3628973960876465],
[2.0014259815216064, 4.294229507446289],
[2.0832109451293945, 4.238814353942871],
[2.149996757507324, 4.194070339202881],
[2.204521894454956, 4.157923698425293],
[2.249027729034424, 4.128708839416504],
[2.285348415374756, 4.105085849761963],
[2.31498384475708, 4.0859761238098145],
[2.339160442352295, 4.070511341094971],
[2.3588807582855225, 4.057991027832031],
[2.3749637603759766, 4.0478515625],
[2.3880786895751953, 4.039637088775635],
[2.3987717628479004, 4.032979965209961],
[2.40748929977417, 4.027583599090576],
[2.414595603942871, 4.023208141326904],
[2.4203879833221436, 4.019659042358398],
[2.4251089096069336, 4.016779899597168],
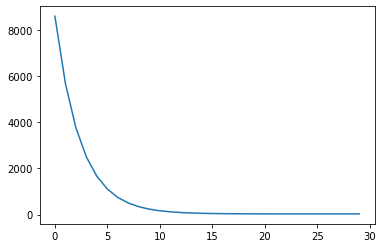
[2.4289560317993164, 4.014443874359131]]- loss 관찰
학습과정을 animation으로 시각화
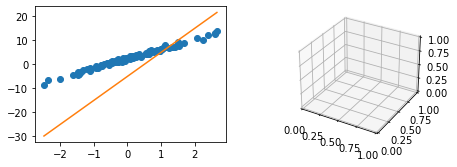
- 왼쪽에는 \((x_i,y_i)\) and \((x_i,\hat{y}_i)\) 을 그리고 오른쪽에는 \(loss(w_0,w_1)\) 을 그릴것임
- 왼쪽그림!
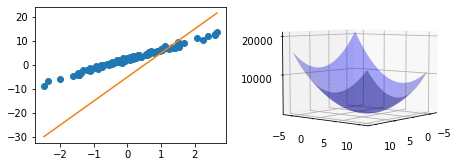
- 오른쪽 그림1: \(loss(w_0,w_1)\)
_w0 = np.arange(-6, 11, 0.5) ## 파란색곡면을 그리는 코드 (시작)
_w1 = np.arange(-6, 11, 0.5)
w1,w0 = np.meshgrid(_w1,_w0)
lss=w0*0
for i in range(len(_w0)):
for j in range(len(_w1)):
lss[i,j]=torch.sum((y-_w0[i]-_w1[j]*x)**2)
ax2.plot_surface(w0, w1, lss, rstride=1, cstride=1, color='b',alpha=0.35) ## 파란색곡면을 그리는 코드(끝)
ax2.azim = 40 ## 3d plot의 view 조절
ax2.dist = 8 ## 3d plot의 view 조절
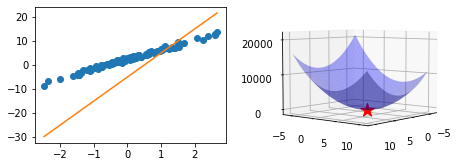
ax2.elev = 5 ## 3d plot의 view 조절 - 오른쪽 그림2: \((w_0,w_1)=(2.5,4)\) 와 \(loss(2.5,4)\) 값 <- loss 함수가 최소가 되는 값 (이거 진짜야? ㅋㅋ)
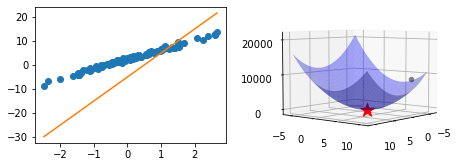
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f87a83a1850>- 오른쪽 그림3: \((w_0,w_1)=(-3.66, 8.81)\) 와 \(loss(-3.66,8.81)\) 값
ax2.scatter(What_history[0][0],What_history[0][1],loss_history[0],color='grey') ## 업데이트되는 What을 표시하는 점 (파란색 동그라미) <mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x7f87a04be210>- 애니메이션
def animate(epoc):
line.set_ydata(yhat_history[epoc])
ax2.scatter(What_history[epoc][0],What_history[epoc][1],loss_history[epoc],color='grey')
return line
ani = animation.FuncAnimation(fig, animate, frames=30)
plt.close()
ani- 함수로 만들자..
def show_lrpr(data,history):
x,y = data
loss_history,yhat_history,What_history = history
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2, projection='3d')
## ax1: 왼쪽그림
ax1.plot(x,y,'o')
line, = ax1.plot(x,yhat_history[0])
## ax2: 오른쪽그림
_w0 = np.arange(-6, 11, 0.5) ## 파란색곡면을 그리는 코드 (시작)
_w1 = np.arange(-6, 11, 0.5)
w1,w0 = np.meshgrid(_w1,_w0)
lss=w0*0
for i in range(len(_w0)):
for j in range(len(_w1)):
lss[i,j]=torch.sum((y-_w0[i]-_w1[j]*x)**2)
ax2.plot_surface(w0, w1, lss, rstride=1, cstride=1, color='b',alpha=0.35) ## 파란색곡면을 그리는 코드(끝)
ax2.scatter(2.5,4,torch.sum((y-2.5-4*x)**2),s=200,color='red',marker='*') ## 최소점을 표시하는 코드 (붉은색 별)
ax2.scatter(What_history[0][0],What_history[0][1],loss_history[0],color='b') ## 업데이트되는 What을 표시하는 점 (파란색 동그라미)
ax2.azim = 40 ## 3d plot의 view 조절
ax2.dist = 8 ## 3d plot의 view 조절
ax2.elev = 5 ## 3d plot의 view 조절
def animate(epoc):
line.set_ydata(yhat_history[epoc])
ax2.scatter(np.array(What_history)[epoc,0],np.array(What_history)[epoc,1],loss_history[epoc],color='grey')
return line
ani = animation.FuncAnimation(fig, animate, frames=30)
plt.close()
return ani\(\alpha\)에 대하여 (\(\alpha\)는 학습률)
(1) \(\alpha=0.0001\): \(\alpha\) 가 너무 작다면? \(\to\) 비효율적이다.
What= torch.tensor([-5.0,10.0],requires_grad=True)
alpha=0.0001
for epoc in range(30):
yhat=X@What ; yhat_history.append(yhat.data.tolist())
loss=torch.sum((y-yhat)**2); loss_history.append(loss.item())
loss.backward()
What.data = What.data-alpha * What.grad; What_history.append(What.data.tolist())
What.grad=None(2) \(\alpha=0.0083\): \(\alpha\)가 너무 크다면? \(\to\) 다른의미에서 비효율적이다 + 위험하다..
What= torch.tensor([-5.0,10.0],requires_grad=True)
alpha=0.0083
for epoc in range(30):
yhat=X@What ; yhat_history.append(yhat.data.tolist())
loss=torch.sum((y-yhat)**2); loss_history.append(loss.item())
loss.backward()
What.data = What.data-alpha * What.grad; What_history.append(What.data.tolist())
What.grad=None(3) \(\alpha=0.0085\)
What= torch.tensor([-5.0,10.0],requires_grad=True)
alpha=0.0085
for epoc in range(30):
yhat=X@What ; yhat_history.append(yhat.data.tolist())
loss=torch.sum((y-yhat)**2); loss_history.append(loss.item())
loss.backward()
What.data = What.data-alpha * What.grad.data; What_history.append(What.data.tolist())
What.grad=None(4) \(\alpha=0.01\)
What= torch.tensor([-5.0,10.0],requires_grad=True)
alpha=0.01
for epoc in range(30):
yhat=X@What ; yhat_history.append(yhat.data.tolist())
loss=torch.sum((y-yhat)**2); loss_history.append(loss.item())
loss.backward()
What.data = What.data-alpha * What.grad; What_history.append(What.data.tolist())
What.grad=None숙제
- 학습률(\(\alpha\))를 조정하며 실습해보고 스크린샷 제출