Lesson 12: 심슨의 역설

Author

최규빈

Published

July 26, 2023

{{< https://youtu.be/playlist?list=PLQqh36zP38-w-fsywiUJa8Dx8hUunE8J1&si=d8A8g_8jNKlqpU9u >}}

강의영상

Imports

import pandas as pd
import numpy as np
from plotnine import *

심슨의 역설

- 버클리대학교의 입학데이터

https://github.com/guebin/DV2023/blob/main/posts/ds.pdf

- 주장: 버클리대학에 gender bias가 존재한다.

1973년 가을학기의 입학통계에 따르면 지원하는 남성이 여성보다 훨씬 많이 합격했고, 그 차이가 너무 커서 우연의 일치라 보기 어렵다.

df=pd.read_csv("https://raw.githubusercontent.com/guebin/DV2022/master/posts/Simpson.csv",index_col=0,header=[0,1])\
.stack().stack().reset_index()\
.rename({'level_0':'department','level_1':'result','level_2':'gender',0:'count'},axis=1)
df

	department	result	gender	count
0	A	fail	male	314
1	A	fail	female	19
2	A	pass	male	511
3	A	pass	female	89
4	B	fail	male	208
5	B	fail	female	7
6	B	pass	male	352
7	B	pass	female	18
8	C	fail	male	204
9	C	fail	female	391
10	C	pass	male	121
11	C	pass	female	202
12	D	fail	male	279
13	D	fail	female	244
14	D	pass	male	138
15	D	pass	female	131
16	E	fail	male	137
17	E	fail	female	299
18	E	pass	male	54
19	E	pass	female	94
20	F	fail	male	149
21	F	fail	female	103
22	F	pass	male	224
23	F	pass	female	238

전체합격률 시각화

A. 시각화1: 전체합격률 시각화 – pandas 초보

- 여성지원자의 합격률

df.pivot_table(index='gender',columns='result',values='count',aggfunc='sum')\
.assign(total = lambda df: df['fail']+df['pass'])\
.assign(rate = lambda df: df['pass']/df['total'])

result	fail	pass	total	rate
gender
female	1063	772	1835	0.420708
male	1291	1400	2691	0.520253

df.query('gender == "female" and result =="pass"')['count'].sum() / df.query('gender == "female"')['count'].sum()

0.420708446866485

- 남성지원자의 합격률

df.query('gender == "male" and result =="pass"')['count'].sum() / df.query('gender == "male"')['count'].sum()

0.5202526941657376

- 시각화

tidydata = pd.DataFrame({'sex':['male','female'],'rate':[0.5202526941657376,0.420708446866485]})
tidydata

	sex	rate
0	male	0.520253
1	female	0.420708

fig = ggplot(tidydata)
col = geom_col(aes(x='sex',y='rate',fill='sex'))
fig + col

B. 시각화1: 전체합격률 시각화 – pandas 고수

tidydata = df.pivot_table(index='gender', columns='result', values='count', aggfunc=sum)\
.assign(rate = lambda df: df['pass'] / (df['fail'] + df['pass']))\
.reset_index()

fig = ggplot(tidydata) 
col = geom_col(aes(x='gender',y='rate',fill='gender'))
fig + col

/tmp/ipykernel_1307301/2552015845.py:1: FutureWarning: The provided callable <built-in function sum> is currently using DataFrameGroupBy.sum. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "sum" instead.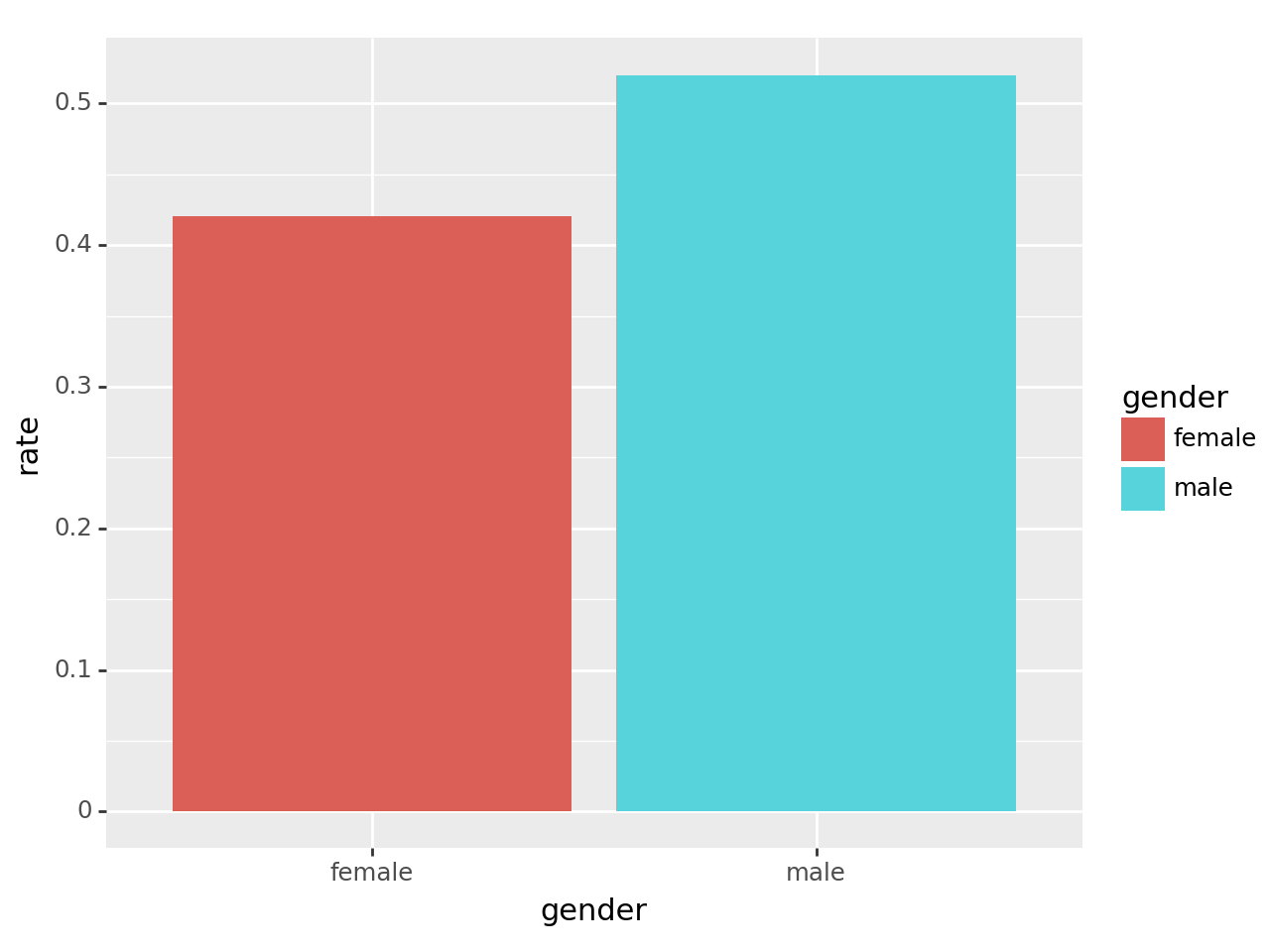

학과별 합격률 시각화

tidydata = df.pivot_table(index=['gender','department'], columns='result',values='count',aggfunc=sum)\
.assign(rate = lambda df: df['pass']/(df['fail']+df['pass']))\
.reset_index()

fig = ggplot(tidydata) 
facet = facet_wrap('department')
col = geom_col(aes(x='gender',y='rate',fill='gender'))
fig + facet + col

/tmp/ipykernel_1307301/2165066459.py:1: FutureWarning: The provided callable <built-in function sum> is currently using DataFrameGroupBy.sum. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "sum" instead.

해석

- 전체합격률: 남자의 합격률이 더 높다. \(\to\) 성차별이 있어보인다(?)

- 학과별합격률: 학과별로 살펴보니 오히려 A,B,F,D의 경우 여성의 합격률이 높다.

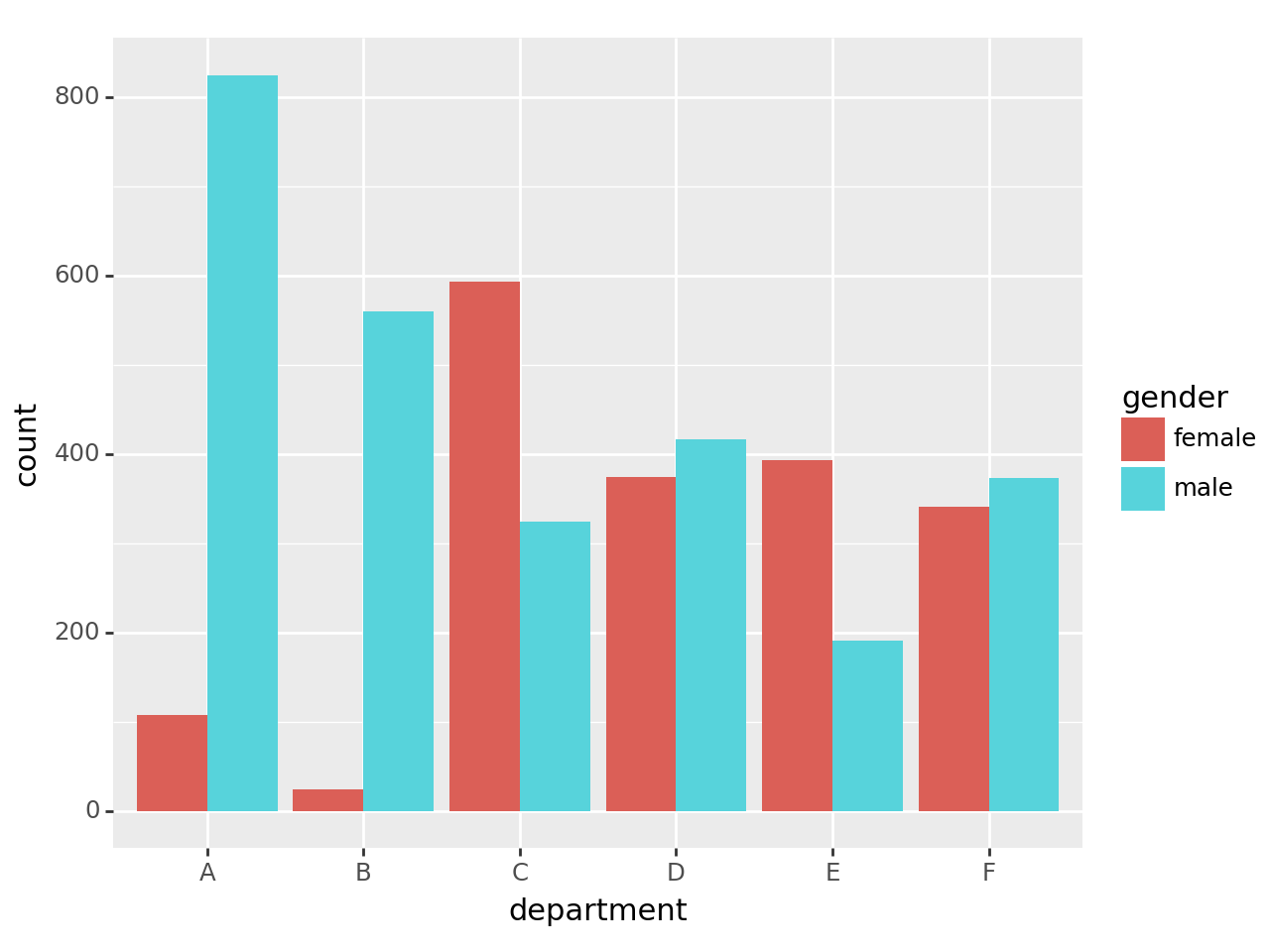
- 교재에서 설명한 이유: 여성이 합격률이 낮은 학과에만 많이 지원하였기 때문

df.pivot_table(index='department', columns='gender', values='count',aggfunc='sum')\
.stack().reset_index().rename({0:'count'},axis=1)

	department	gender	count
0	A	female	108
1	A	male	825
2	B	female	25
3	B	male	560
4	C	female	593
5	C	male	325
6	D	female	375
7	D	male	417
8	E	female	393
9	E	male	191
10	F	female	341
11	F	male	373

tidydata = df.pivot_table(index='department', columns='gender', values='count',aggfunc='sum')\
.stack().reset_index().rename({0:'count'},axis=1)

 
fig = ggplot(tidydata) 
col = geom_col(aes(x='department',y='count',fill='gender'),position='dodge')
fig+col

더 극단적인 예시

df = pd.read_csv("https://raw.githubusercontent.com/guebin/DV2022/master/posts/Simpson2.csv")
df

	department	result	gender	count
0	A	fail	female	0
1	A	fail	male	100
2	A	pass	female	1
3	A	pass	male	900
4	B	fail	female	400
5	B	fail	male	1
6	B	pass	female	600
7	B	pass	male	1

- 전체합격률 조사

display(
    f"합격률(여성):{601/1001:.4f}",
    df[df.gender=='female'],
    f"합격률(남성):{901/1002:.4f}",
    df[df.gender=='male'],
)

'합격률(여성):0.6004'

	department	result	gender	count
0	A	fail	female	0
2	A	pass	female	1
4	B	fail	female	400
6	B	pass	female	600

'합격률(남성):0.8992'

	department	result	gender	count
1	A	fail	male	100
3	A	pass	male	900
5	B	fail	male	1
7	B	pass	male	1

- 학과별 합격률 조사

df

	department	result	gender	count
0	A	fail	female	0
1	A	fail	male	100
2	A	pass	female	1
3	A	pass	male	900
4	B	fail	female	400
5	B	fail	male	1
6	B	pass	female	600
7	B	pass	male	1

display(
    f"합격률(A학과,여성):{1/1:.4f}",
    f"합격률(A학과,남성):{900/1000:.4f}",
    f"합격률(B학과,여성):{600/1000:.4f}",
    f"합격률(B학과,여성):{1/2:.4f}",
)

'합격률(A학과,여성):1.0000'

'합격률(A학과,남성):0.9000'

'합격률(B학과,여성):0.6000'

'합격률(B학과,여성):0.5000'