Lesson 11: 아이스크림을 많이 먹으면 걸리는 병 (draft)

Author

최규빈

Published

July 26, 2023

{{< https://youtu.be/playlist?list=PLQqh36zP38-yJd2E9jkWYAZxBh7W5faep&si=wY4BPM11_6EzCKNy >}}

Imports

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from plotnine import *

아이스크림을 많이 먹으면 걸리는 병 (1)

- ref- 데이터 과학자의 사고법: 더 나은 선택을 위한 통계학적 통찰의 힘

  • 구매할만한 책입니다

- 내용요약

  • 여름 \(\to\) 수영장 \(\to\) 소아마비
  • 여름 \(\to\) 아이스크림
  • 아이스크림과 소아마비는 상관관계가 높다: 아이스크림 성분중에서 소아마비를 유발하는 유해물질이 있을 것이다 (?)

- 아래와 같이 모형을 간단하게 하자.

  • 온도 \(\to\) 소아마비
  • 온도 \(\to\) 아이스크림

Toy exam

- 교재의 예제상황은 예를들면 아래와 같다.

(숨은진짜상황1)

\[\text{아이스크림 판매량} = 20 + 2 \times \text{온도} + \text{오차}\]

np.random.seed(1) 
temp = np.array([-10.2, -5.2, 0.1, 10.1, 12.2, 14.7, 
                25.4, 26.8, 28.9, 35.1, 32.2, 34.6])
eps = np.random.normal(size=12,scale=5)
icecream = 20 + temp * 2 + eps
plt.plot(temp,icecream,'o')

(숨은진짜상황2)

\[\text{소아마비 반응수치} = 30 + 0.5 \times \text{온도} + \text{오차}\]

np.random.seed(2) 
eps = np.random.normal(size=12,scale=5) 
disease = 30+ temp * 0.5 + eps
plt.plot(temp,disease,'o')

(우리가 데이터로부터 관측한 상황)

- 아이스크림과 질병의 산점도를 그려보자.

plt.plot(icecream,disease,'o')

- 아이스크림 중 어떠한 물질이 소아마비를 일으키는것이 분명하므로 (인과성이 분명해보이니까) 아래와 같은 모형을 세우자. <– 여기서부터 틀렸음

\[{\tt disease}_i =\beta_0 +\beta_1 {\tt icecream}_i +\epsilon_i,\quad \textbf{for} ~~ i=1,2,\dots, 12\]

- 적절한 \(\beta_0\)와 \(\beta_1\)을 추정하면 우리는 아이스크림과 소아마비의 관계를 알 수 있다. <– 틀린주장

  • 틀린 모형
  • 도데체 우리가 뭘 잘못했는가?

- 두 변수 사이에 상관관계가 있어도 실제 원인은 다른 변수에 숨겨져 있는 경우가 많다.

(ex1)

  • 온도 \(\to\) 익사
  • 온도 \(\to\) 아이스크림
  • 아이스크림과 익사자도 양의 상관관계에 있을것이다.
  • 아이스크림을 먹이면 물에 빠져 죽는다 \(\to\) 틀린주장
  • 사실 기온이 숨겨진 원인이다. 기온이 증가하면 아이스크림 판매량도 증가하고 폭염때문에 익사사고율도 높아지는 구조이다.

(ex2)

  • 인구수 \(\to\) 교회
  • 인구수 \(\to\) 범죄건수
  • 지역별 교회와 범죄건수를 살펴보면 상관관계가 높게 나올것임
  • 교회를 지으면 범죄건수도 증가한다? \(\to\) 틀린주장
  • 사실 인구가 숨겨진 요인임

- ex2, ex1에 대하여 바른 분석을 하려면?

  • ex2: 인구가 비슷한 도시끼리 묶어서 비교해보면 교회와 범죄의 건수는 양의 상관관계에 있지 않을것임
  • ex1: 온도가 비슷한 그룹끼리 묶어보자.

- 올바른 분석: 온도가 비슷한 그룹끼리 묶어서 그려보자. \(\to\) 상관계수가 줄어들 것이다.

plt.plot(icecream[:6],disease[:6],'o')

plt.plot(icecream[6:],disease[6:],'o')

  • 진짜로 선형관계가 약해졌다..

아이스크림을 많이 먹으면 걸리는 병 (2)

자료생성: 좀 더 그럴듯한 자료 (만들기)

- 지난 시간의 toy example은 데이터가 너무 작아서 억지스러움 \(\to\) 기상자료개방포털, 회원가입해야 자료받을 수 있음.

_df = pd.read_csv('https://raw.githubusercontent.com/guebin/DV2022/master/posts/temp.csv')
_df
지점번호 지점명 일시 평균기온(℃) 최고기온(℃) 최고기온시각 최저기온(℃)
0 146 전주 2020-01-01 -0.5 4.3 15:09 -6.4
1 146 전주 2020-01-02 1.4 6.5 14:12 -3.0
2 146 전주 2020-01-03 2.6 7.6 13:32 -0.5
3 146 전주 2020-01-04 2.0 7.7 13:51 -2.6
4 146 전주 2020-01-05 2.5 8.6 14:05 -3.2
... ... ... ... ... ... ... ...
651 146 전주 2021-10-13 19.9 25.5 14:29 15.6
652 146 전주 2021-10-14 20.4 25.5 13:36 17.0
653 146 전주 2021-10-15 18.3 22.0 13:47 15.7
654 146 전주 2021-10-16 12.8 17.4 0:01 6.5
655 146 전주 2021-10-17 6.7 12.4 15:18 2.2

656 rows × 7 columns

- 평균기온만 선택

pd.Series(_df.columns)
0       지점번호
1        지점명
2         일시
3    평균기온(℃)
4    최고기온(℃)
5     최고기온시각
6    최저기온(℃)
dtype: object
temp = np.array(_df.iloc[:,3])
temp[:5]
array([-0.5,  1.4,  2.6,  2. ,  2.5])

# 숨은진짜상황1: 온도 \(\to\) 아이스크림 판매량

- 아래와 같은 관계가 있다고 하자.

\[\text{아이스크림 판매량} = 20 + 2 \times \text{온도} + \text{오차}\]

np.random.seed(1)
eps = np.random.normal(size=len(temp), scale=10) 
icecream = 20 + 2*temp + eps
plt.plot(temp,icecream,'o',alpha=0.3)
plt.xlabel("temp",size=15)
plt.ylabel("icecream",size=15)
Text(0, 0.5, 'icecream')

# 숨은진짜상황2: 온도 \(\to\) 소아마비 반응수치

- 아래와 같은 관계가 있다고 하자.

\[\text{소아마비 반응수치} = 30 + 0.5 \times \text{온도} + \epsilon\]

np.random.seed(2) 
eps=np.random.normal(size=len(temp),scale=1)
disease= 30 + 0.5 * temp + eps
plt.plot(temp,disease,'o',alpha=0.3)
plt.xlabel("temp",size=15)
plt.ylabel("disease",size=15)
Text(0, 0.5, 'disease')

# 우리가 관측한 상황 (온도는 은닉되어있음)

plt.plot(icecream,disease,'o',alpha=0.3)
plt.xlabel("icecream",size=15)
plt.ylabel("disease",size=15)
Text(0, 0.5, 'disease')

직관: 여름만 뽑아서 plot 해보자.

- temp>25 (여름으로 간주) 인 관측치만 플랏

plt.plot(icecream[temp>25],disease[temp>25], 'o', color='C1') ## 평균기온이 25도가 넘어가면 여름이라 생각

- 전체적인 산점도

fig , ((ax1,ax2), (ax3,ax4)) = plt.subplots(2,2,figsize=(8,6)) 
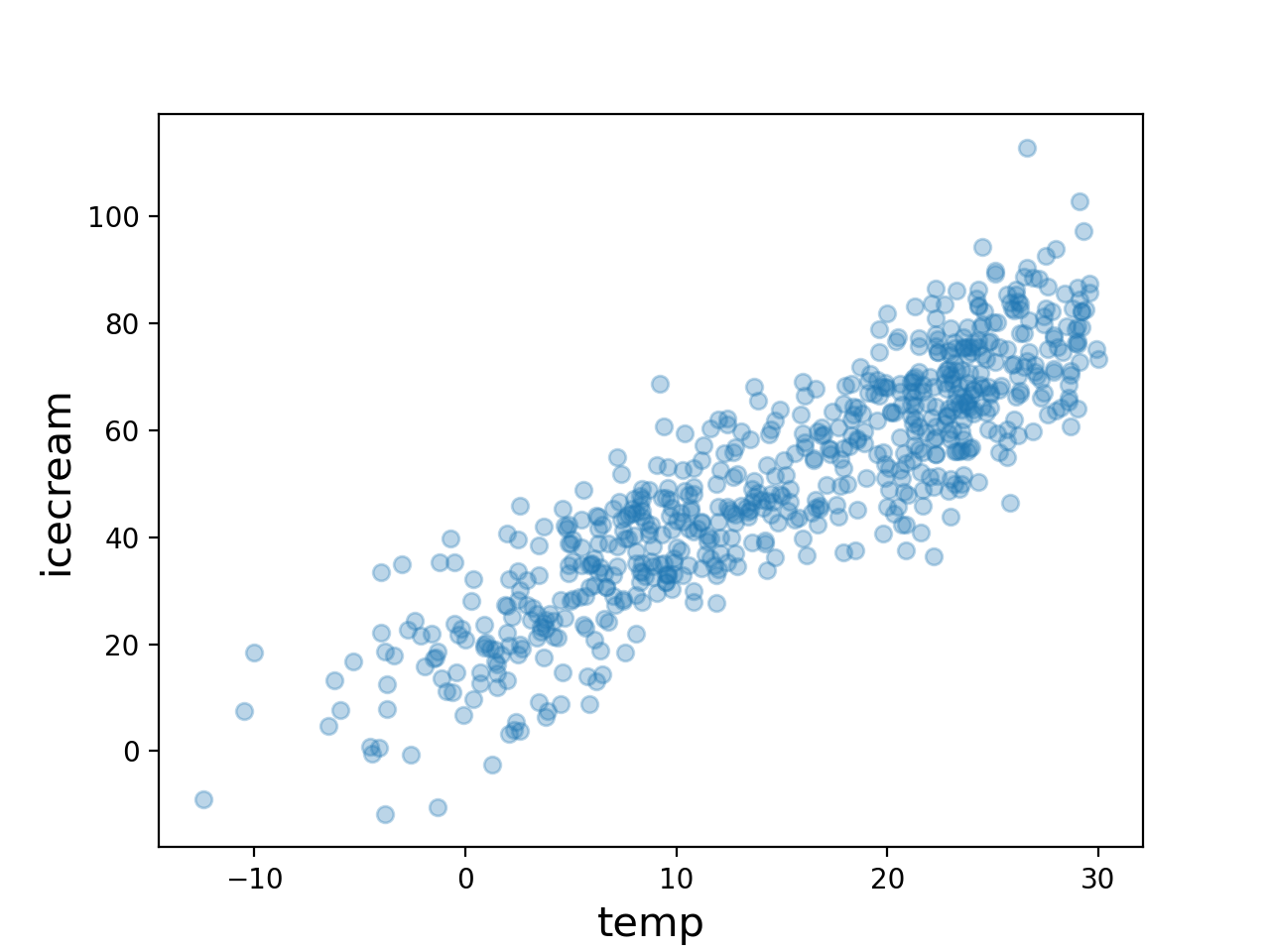
ax1.plot(temp,icecream,'o',alpha=0.2); ax1.set_xlabel('temp'); ax1.set_ylabel('icecream'); ax1.set_title("hidden1")
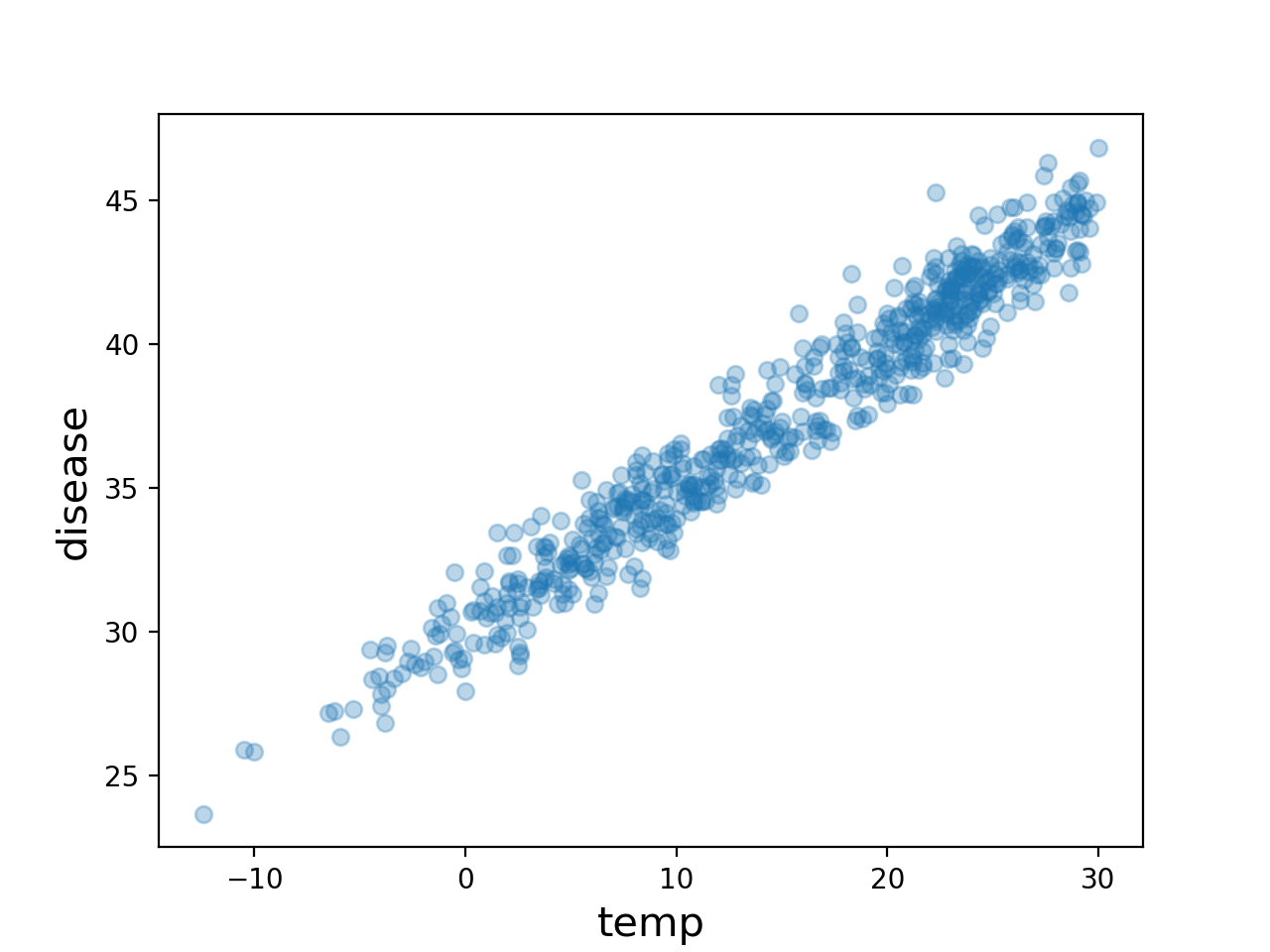
ax2.plot(temp,disease,'o',alpha=0.2); ax2.set_xlabel('temp'); ax2.set_ylabel('disease'); ax2.set_title("hidden2")
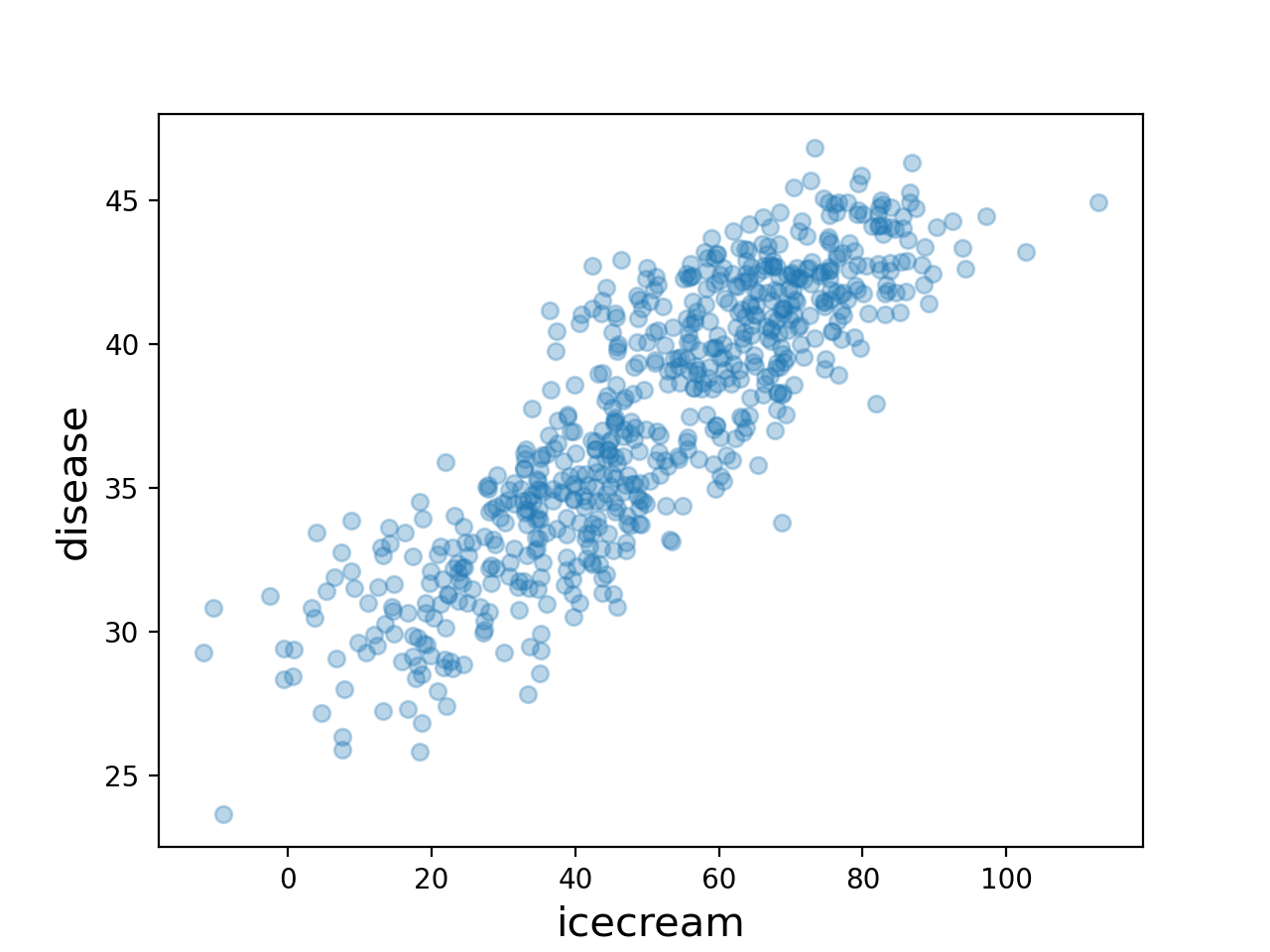
ax3.plot(icecream,disease,'o',alpha=0.2); ax3.set_xlabel('icecream'); ax3.set_ylabel('disease'); ax3.set_title("observed")
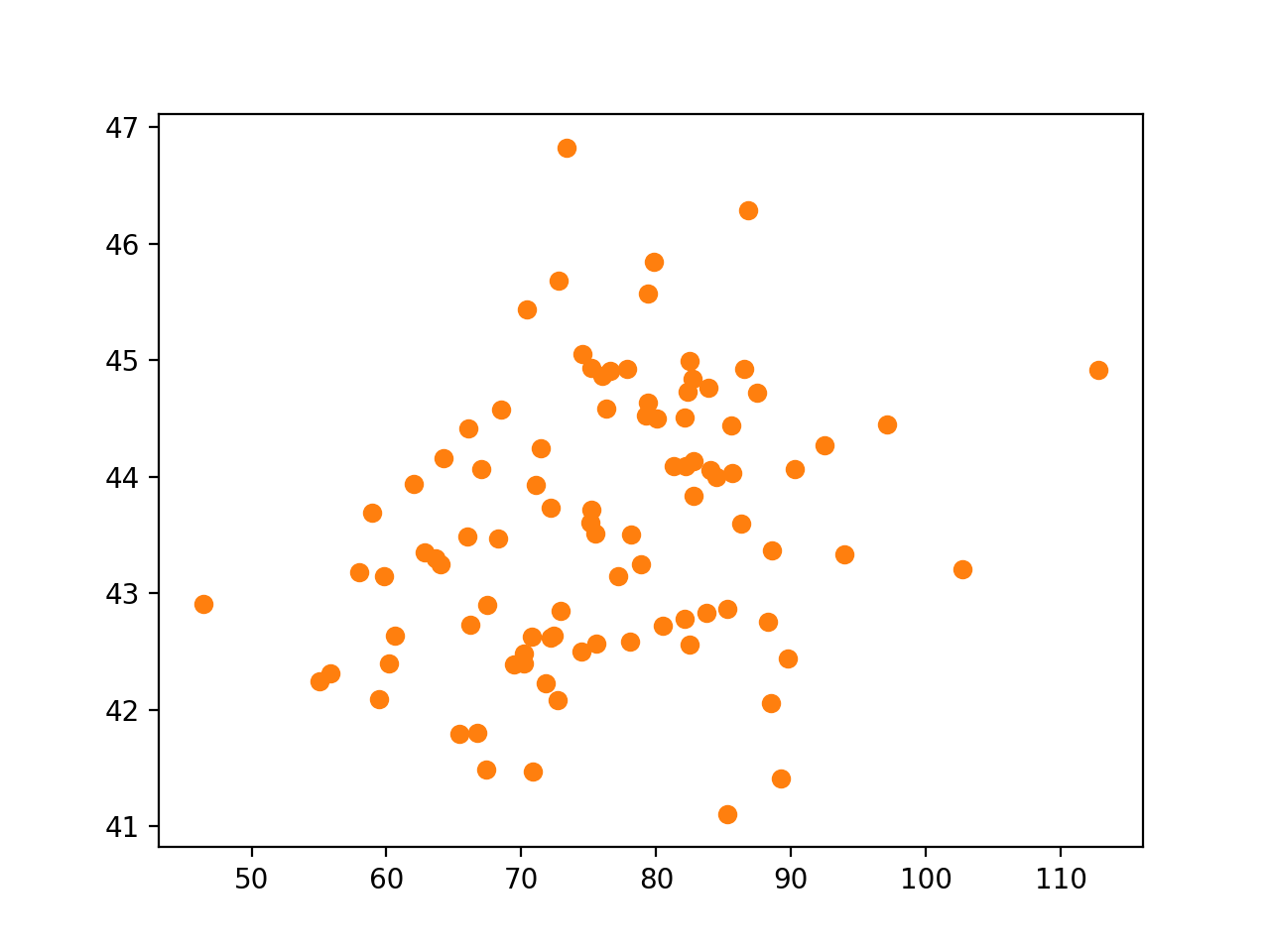
ax4.plot(icecream,disease,'o',alpha=0.2); ax4.set_xlabel('icecream'); ax4.set_ylabel('disease'); ax4.set_title("observed")
ax4.plot(icecream[temp>25],disease[temp>25],'o',label='temp>25')
ax4.legend()
fig.tight_layout()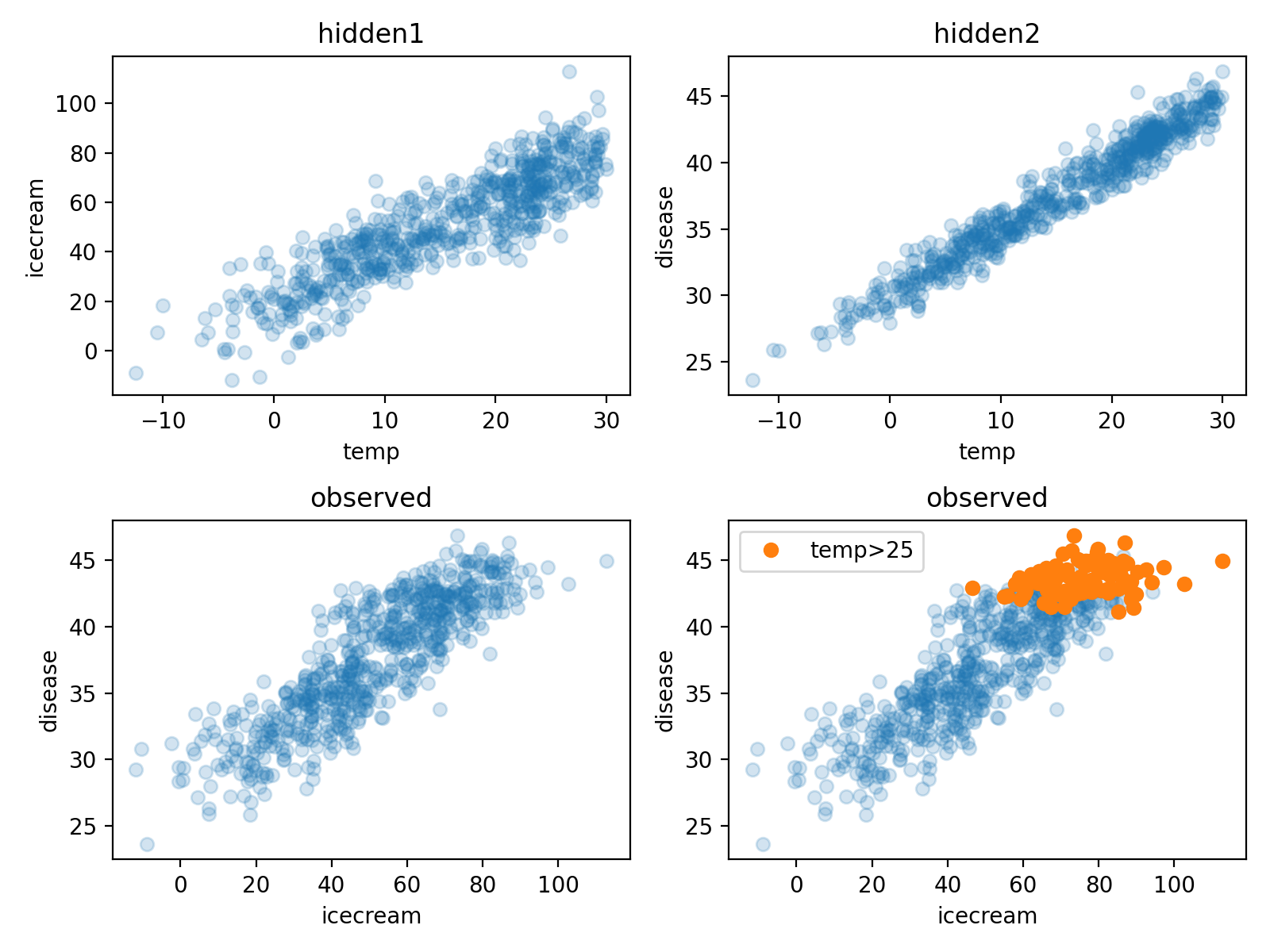

ggplot: 온도구간을 세분화 하여 시각화

- 목표: 모든 온도구간에 대하여 각각 색을 다르게 하여 그려보자.

  • 사실 지금 변수는 온도, 아이스크림판매량, 소아마비
  • 온도가 유사한 지역을 색으로 묶으면 3차원 플랏이 가능함
df = pd.DataFrame({'temp':temp,'icecream':icecream,'disease':disease})
df
temp icecream disease
0 -0.5 35.243454 29.333242
1 1.4 16.682436 30.643733
2 2.6 19.918282 29.163804
3 2.0 13.270314 32.640271
4 2.5 33.654076 29.456564
... ... ... ...
651 19.9 68.839992 39.633906
652 20.4 76.554679 38.920443
653 18.3 68.666079 39.882650
654 12.8 42.771364 36.613159
655 6.7 30.736731 34.902513

656 rows × 3 columns

fig = ggplot(df.assign(temp_cut = pd.qcut(df.temp,7)))
point = geom_point(aes(x='icecream',y='disease',color='temp_cut'),alpha=0.2)
line = geom_smooth(aes(x='icecream',y='disease',color='temp_cut'))
line2 = geom_smooth(aes(x='icecream',y='disease'))
fig+point+line+line2
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.
/home/cgb2/anaconda3/envs/ag/lib/python3.10/site-packages/plotnine/stats/smoothers.py:330: PlotnineWarning: Confidence intervals are not yet implemented for lowess smoothings.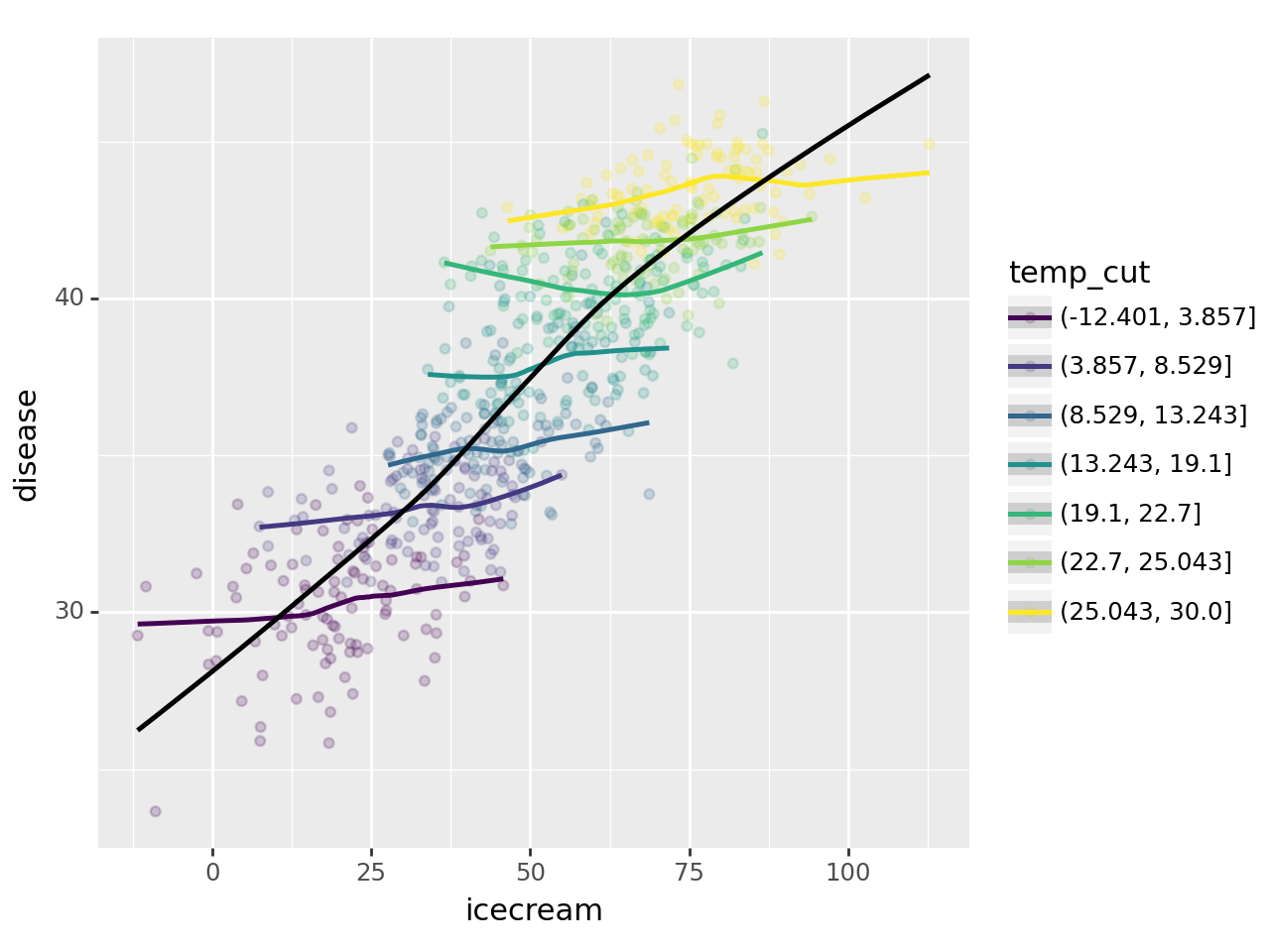

  • 각 온도별로 추세선은 거의 기울기가 0이다. \(\to\) 온도가 비슷한 구간별로 묶어서 보니까 상관관계가 없다는 거!
  • 아이스크림 판매량과 소아마비의 corr은 유의미해보이지만, 온도를 통제하였을 경우 아이스크림 판매량과 소아마비의 partial corr은 유의미해보이지 않음.

# 해석

- 해피앤딩: 온도를 통제하니까 아이스크림과 질병은 관련이 없어보인다. \(\to\) 아이스크림을 먹으면 소아마비를 유발한다는 이상한 결론이 나올뻔 했지만 우리는 온도라는 흑막을 잘 찾았고 결과적으로 “온도->아이스크림판매량,소아마비” 이라는 합리적인 진리를 얻을 수 있었다.

  • 온도와 같은 변수를 은닉변수라고 한다.

- 또 다른 흑막? 고려할 흑막이 온도뿐이라는 보장이 어디있지? 사실 흑막2, 흑막3이 있어서 그런 흑막들을 고려하다보니까 아이스크림과 소아마비사이의 상관관계가 다시 보이면 어떡하지?

  • 이러한 이유 때문에 상관계수로 인과성을 유추하는건 사실상 불가능.
  • 그런데 이론적으로는 “세상의 모든 은닉변수를 통제하였을 경우에도 corr(X,Y)의 값이 1에 가깝다면 그때는 인과성이 있다고 봐도 무방함, (물론 이 경우에도 무엇이 원인인지는 통계적으로 따지는것이 불가)” 이라고 주장할 수 있다. 즉 모든 흑막을 제거한다면 “상관성=인과성”이다.

- 실험계획법, 인과추론: 세상의 모든 흑막을 제거하는건 상식적으로 불가능

  • 피셔의주장(실험계획법): 그런데 실험계획을 잘하면 흑막을 제거한 효과가 있음 (무작위로 사람뽑아서 담배를 피우게 한다든가)
  • 인과추론: 실험계획이 사실상 불가능한 경우가 있음 \(\to\) 모인 데이터에서 최대한 흑막2,3,4,.. 등이 비슷한 그룹끼리 “매칭”을 시킨다!