01wk-2: 파이썬은 좋은 계산기다 (1)

Author

최규빈

Published

March 8, 2024

1. 강의영상

2. Imports

import numpy as np
import matplotlib.pyplot as plt

3. 파이썬은 좋은 계산기이다.

- 아주 어려운 연산도 척척해줌.

np.cos(np.pi) # 삼각함수의 값 계산
-1.0
np.mean(np.array([1,0,1])) # 평균을 계산
0.6666666666666666

- 변수저장 가능

\(x\)에 따라 아래의 값을 계산하고 싶다면?

  • \(y=2x-5\)
  • \(\frac{e^y}{1+e^y}\)
x = 2 
y = 2*x -5 
np.exp(y) / (1+np.exp(y))
0.2689414213699951

- 그림도 그려줌..

x = np.array([1,2,3,4,5])
y = x**2 - 2*x + 1 
plt.plot(x,y,'o')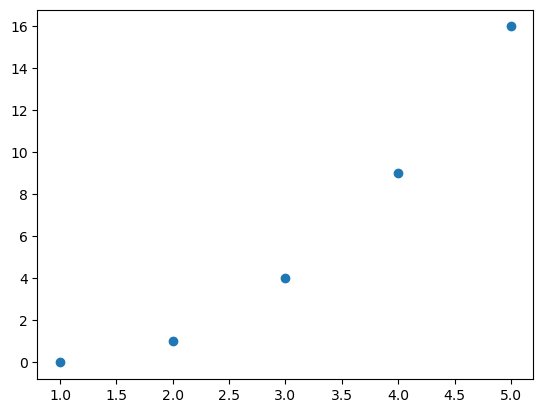

4. 2024 수능 – 1,2,4,6,23

(풀이)

(24)**(1/3) * 3**(2/3)
6.0

(풀이)

h = 0.0000001
def f(x):
    return 2*x**3 - 5*x**2 + 3
(f(2+h)-f(2))/h
4.000000721759989

(풀이)

a = 1
3*2-a, 2**2 + a
(5, 5)

(풀이)

r = 0.5
an = np.array([(3/4)/(r**4),(3/4)/(r**3),(3/4)/(r**2),(3/4)/r,3/4])
Sn = np.cumsum(an)
Sn[3] - Sn[1], 3*an[3]
(4.5, 4.5)
an
array([12.  ,  6.  ,  3.  ,  1.5 ,  0.75])
12+6
18

(풀이)

x = 0.0001 
np.log(1+3*x)/np.log(1+5*x)
0.600059983005448

5. 2024 수능 - 3,7,24

(풀이)

theta = np.linspace(3/2*np.pi, 2*np.pi, 100)
plt.plot(theta,np.sin(-theta),label=r"$y=\sin(-\theta)$")
plt.plot(theta,np.sin(-theta)*0+1/3,'.',label=r"$y=\frac{1}{3}$")
plt.legend()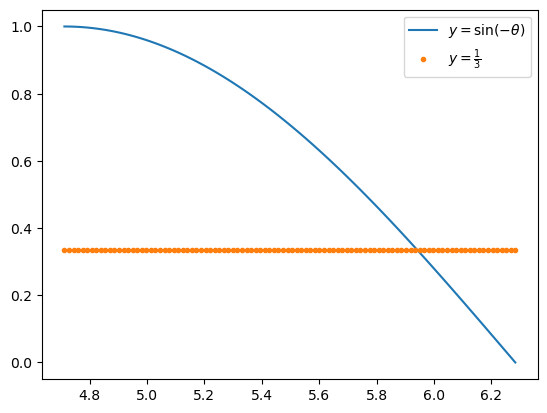

plt.plot(np.sin(-theta),label=r"$y=\sin(-\theta)$")
plt.plot(np.sin(-theta)*0+1/3,'.',label=r"$y=\frac{1}{3}$")
plt.legend()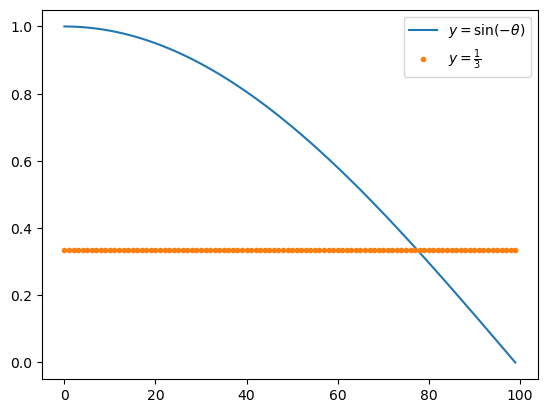

plt.plot(np.sin(-theta)[70:80],'o')
plt.plot(np.sin(-theta)[70:80]*0+1/3,'o')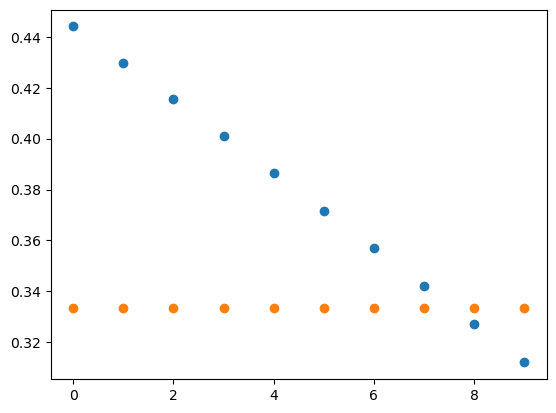

np.sin(-theta)[70:80] # 이중에서 0.33333... 에 가장 가까운것은 끝에서 두번째 
array([0.44406661, 0.42979491, 0.41541501, 0.40093054, 0.38634513,
       0.37166246, 0.35688622, 0.34202014, 0.32706796, 0.31203345])
np.sin(-theta)[78] # 이 값이 0.3333에 가장 가까움
0.32706796331742194
theta[78] # 이것이 theta 값
5.949986086344305
np.tan(5.949986086344305) # 이게 답이다
-0.34610336503441297
-np.sqrt(2)/2, -np.sqrt(2)/4, -1/4, 1/4, np.sqrt(2)/4 # 보기와 비교하면???
(-0.7071067811865476, -0.3535533905932738, -0.25, 0.25, 0.3535533905932738)

(풀이)

x=0
#def f(x):
#    return (1/3)*x**3 - 2*x**2 -12*x +4 
f = lambda x: (1/3)*x**3 - 2*x**2 -12*x +4
x = np.linspace(-5,8,101)
plt.plot(x,f(x),'.')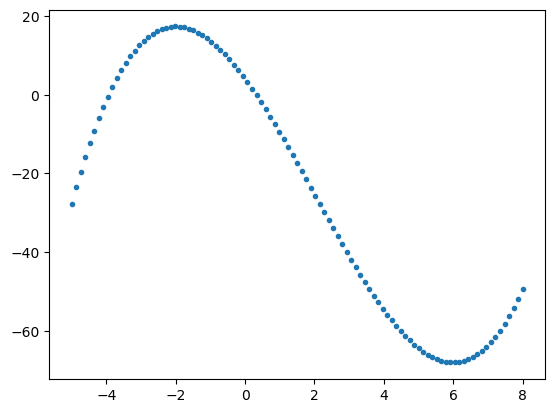

arr = np.array([1,2,33,-3,2,44])
np.argmax(arr)
5
np.argmax(f(x)), np.argmin(f(x))
(23, 85)
x[85]- x[23]
8.06

(풀이)

t = np.linspace(1/100,1,100)
x = np.log(t**3+1)
y = np.sin(np.pi*t)
plt.plot(x,y,'.')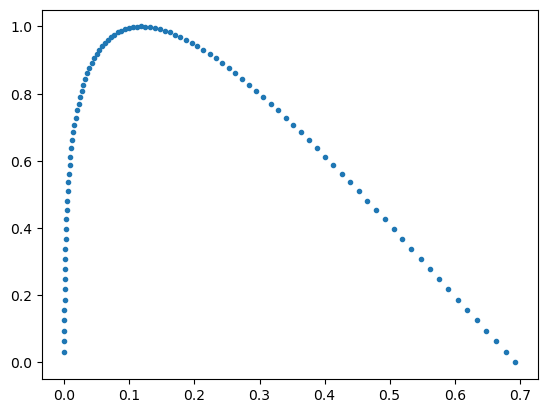

x[-1],y[-1] # 마지막점
(0.6931471805599453, 1.2246467991473532e-16)
x[-2],y[-2] # 마지막에서 두번째점
(0.6781853078827329, 0.031410759078128236)
(y[-2]-y[-1])/(x[-2]-x[-1]) 
-2.0993868719367015
-1/3*np.pi, -2/3*np.pi, -np.pi, - 4/3*np.pi, -5/3*np.pi # 따라서 답은 2번
(-1.0471975511965976,
 -2.0943951023931953,
 -3.141592653589793,
 -4.1887902047863905,
 -5.235987755982989)

6. 파이썬 문법복습

A. 함수를 선언하는 두 가지 방법

- 방법1: def를 이용하는 방법

def f(x):
    return x+1
f(3)
4

- 방법2: lambda를 사용하는 방법

f = lambda x: x+1
f(3)
4

B. list와 np.array의 차이점

- 리스트는 수학친화적이지 않다.

lst1 = [1,2,3]
lst2 = [-1, -2, -3]
lst1+lst2
[1, 2, 3, -1, -2, -3]

- 넘파이는 수학친화적이다.

arr1 = np.array([1,2,3])
arr2 = np.array([-1, -2, -3])
arr1+arr2
array([0, 0, 0])

C. 인덱스로 벡터의 원소를 뽑는 방법

x = [11,22,33,-22,-33,-44]

- 첫번째 원소를 뽑고 싶다면?

x[0]
11

- 두번째 원소를 뽑고 싶다면?

x[1]
22

- 마지막 원소를 뽑고 싶다면?

x[5]
-44
x[-1]
-44

- 마지막에서 두번째 원소를 뽑고 싶다면?

x[4]
-33
x[-2]
-33

- index = 0,1,2 에 해당하는 원소만 추출

x[0:3] # 마지막 인덱스 3은 포함되지 않음 
[11, 22, 33]

- index = 2,3,4 에 해당하는 원소만 추출

x[2:5] # 2,3,4에 해당하는 인덱스만 추출
[33, -22, -33]

- x[0:3]와 같이 처음 시작점이 0인 경우 생략가능

x[:3] 
[11, 22, 33]

- x[k:]와 같은 코드는 index=k에서 끝까지 뽑는다는 의미이다.

x[3:6] #3,4,5
[-22, -33, -44]
x[3:]
[-22, -33, -44]

D. np.cumsum(), np.cumprod()

- 누적합

arr = np.array([1,-1,1,-1,1,-1])
arr
array([ 1, -1,  1, -1,  1, -1])
np.cumsum(arr)
array([1, 0, 1, 0, 1, 0])

- 누적곱

arr = np.array([1,2,3,4])
arr
array([1, 2, 3, 4])
np.cumprod(arr)
array([ 1,  2,  6, 24])

E. plt.plot()

- 예시1: \(x\)없이 그리기 (라인)

y=[2,3,5,2]
plt.plot(y)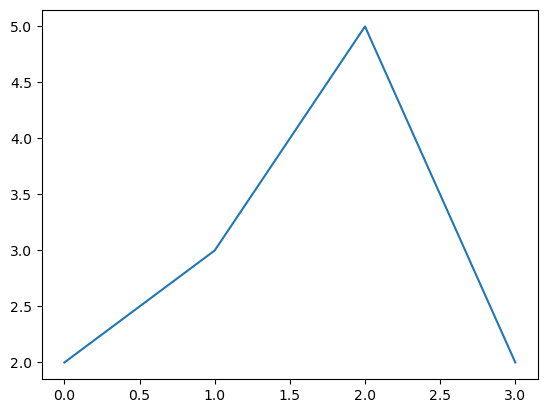

- 예시2: \(x\)없이 그리기 (점)

y=[2,3,5,2]
plt.plot(y,'o')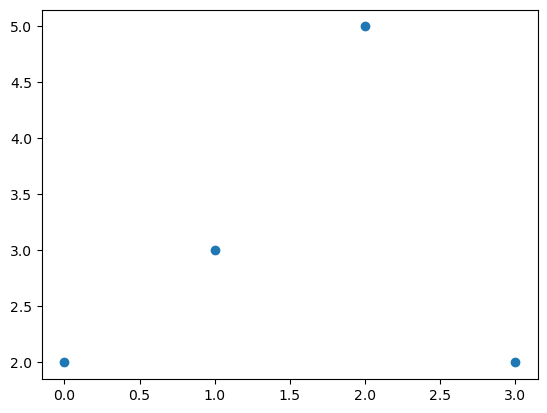

- 예시3: \((x,y)\)를 전달하여 그리기(점)

x=[20,21,22,23]
y=[2,3,5,2]
plt.plot(x,y,'o')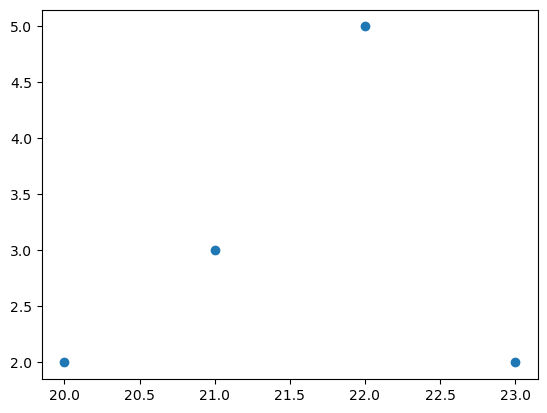

- 예시4: 겹쳐서 그리기

x=[20,21,22,23]
y1=[2,3,5,-2]
y2=[2.5 ,3.5 ,5.5 , -2.5]
plt.plot(x,y1,'--o')
plt.plot(x,y2,'--o')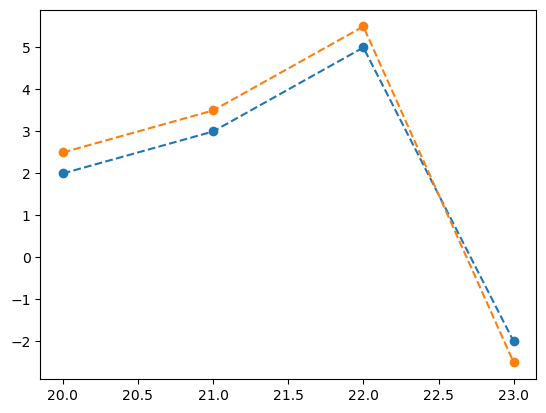

- 예시5: 겹쳐서 그리기 + 라벨

x=[20,21,22,23]
y1=[2,3,5,-2]
y2=[2.5 ,3.5 ,5.5 , -2.5]
plt.plot(x,y1,'--o',label="y1")
plt.plot(x,y2,'--o',label="y2")
plt.legend()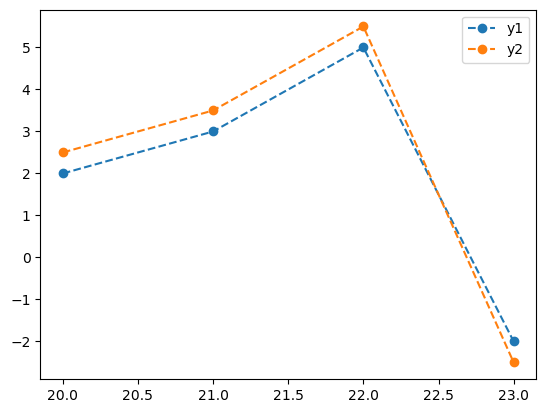

- 예시5: 겹쳐서 그리기 + latex 라벨

x=[20,21,22,23]
y1=[2,3,5,-2]
y2=[2.5 ,3.5 ,5.5 , -2.5]
plt.plot(x,y1,'--o',label=r"$y_1$")
plt.plot(x,y2,'--o',label=r"$y_2$")
plt.legend()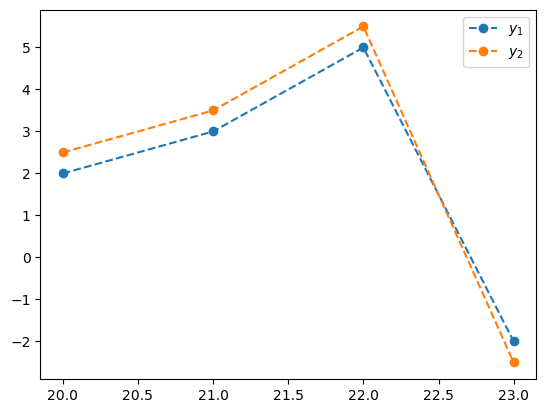

  • latex수식은 이 수업에서 필수사항은 아님
  • latex수식을 사용할 수 없어도 시험점수를 획득할때 아무런 불이익이 없음.

F. np.argmax, np.argmin

- 예시1

arr = np.array([1,2,3,2,1,0])
arr
array([1, 2, 3, 2, 1, 0])
np.argmax(arr),np.argmin(arr)
(2, 5)

# 예제 – 두 함수의 교점

\(-1 \leq x \leq 3\) 에서

  • \(f(x)=(x-1)^2\) 와
  • \(g(x)=-2x+5\)

의 교점의 좌표를 구하여라.

(풀이)

x = np.linspace(-1,3,101)
f = (x-1)**2
g = -2*x+5 
plt.plot(x,f,label=r"$f(x)=(x-1)^2$")
plt.plot(x,g,label=r"$g(x)=-2x+5$")
plt.legend()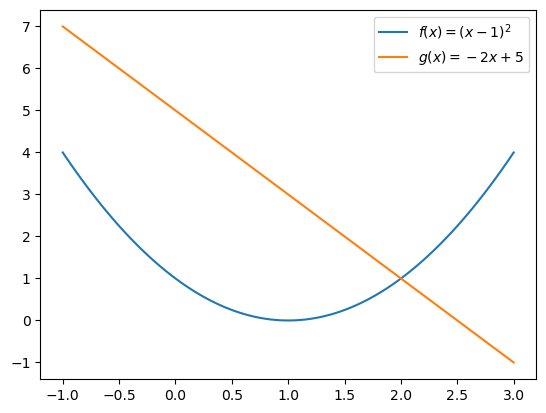

x[np.argmin(abs(f-g))]
2.0
2,(2-1)**2
(2, 1)
  • 이것이 교점의 좌표

7. 숙제

- \(x=3\)일때

\[\frac{e^x}{1+e^x}\]

값을 계산하는 코드를 작성하고 LMS에 제출하라.

.ipynb파일형태로 LMS에 제출할 것. (Quiz제출 연습용임. 제출방법이 익숙하지 않은 학생은 꼭 질문할것. 이 숙제는 제출하지 않아도 감점없음)