14wk-2: 연습문제 (4)

Author

최규빈

Published

December 4, 2025

MLE 기반 추정

1. 아래는 정규분포 \(N(0,1)\)에서 중심 \(\mu=0\)을 추정하는 시뮬레이션 결과이다. (단, \(n=100\), \(m=10000\))

  • \(n\)개의 샘플 \(x_1, \ldots, x_{n}\)을 추출하여 A방식과 B방식으로 각각 \(\hat\mu_x\)를 계산
  • \(n\)개의 샘플 \(y_1, \ldots, y_{n}\)을 독립적으로 추출하여 A방식과 B방식으로 각각 \(\hat\mu_y\)를 계산
  • 위 과정을 \(m\)번 반복하여 \((\hat\mu_x, \hat\mu_y)\)를 산점도로 표시 (따라서 점은 각 방식별로 \(m\)개씩 있음)
방식 추정량
A (파란색) 상위 10%, 하위 10%를 제외한 후 평균 (trimmed mean)
B (주황색) 표본평균 \(\bar{x}\)

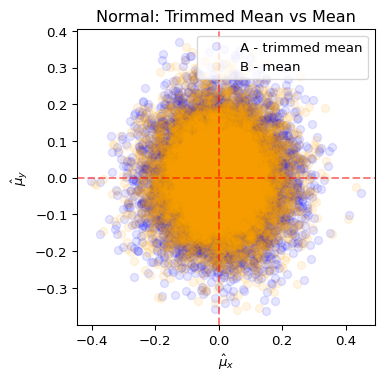
그림을 해석한 것으로 옳은 것을 모두 고르라.

  1. A방식은 MLE에 근거한 방식이다.
  2. B방식은 MLE에 근거한 방식이다.
  3. B방식이 A방식보다 더 효율적이다. 왜냐하면 분포와 상관없이 항상 표본평균으로 모평균을 추정하는 것이 합리적이기 때문이다.
  4. \(n\)이 커진다면 두 방식 모두 \(m\)개의 점들이 점점 중앙으로 몰리게 될 것이다.

2. 아래는 정규분포 \(N(0,1)\)에서 중심 \(\mu=0\)을 추정하는 시뮬레이션 결과이다. (단, \(n=100\), \(m=10000\))

  • \(n\)개의 샘플 \(x_1, \ldots, x_{n}\)을 추출하여 A방식과 B방식으로 각각 \(\hat\mu_x\)를 계산
  • \(n\)개의 샘플 \(y_1, \ldots, y_{n}\)을 독립적으로 추출하여 A방식과 B방식으로 각각 \(\hat\mu_y\)를 계산
  • 위 과정을 \(m\)번 반복하여 \((\hat\mu_x, \hat\mu_y)\)를 산점도로 표시 (따라서 점은 각 방식별로 \(m\)개씩 있음)
방식 추정량
A (파란색) 중앙값 (median)
B (주황색) 표본평균 (mean)

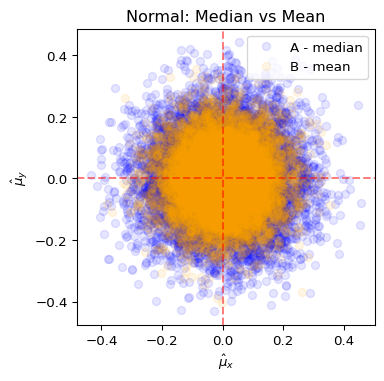
그림을 해석한 것으로 옳은 것을 모두 고르라.

  1. 이 경우 중앙값에 의한 추정이 MLE에 근거한 추정법이다.
  2. 이 경우 표본평균에 의한 추정이 MLE에 근거한 추정법이다.
  3. \(n\)이 작을 때는 평균이 더 효율적이지만, \(n\)이 커지면 중앙값이 더 효율적이 된다.
  4. 정규분포에서 중앙값과 평균은 항상 동일한 추정값을 가진다.

3. 아래는 균등분포 \(U(0,1)\)에서 중심 \(\mathbb{E}(X)=0.5\)를 추정하는 시뮬레이션 결과이다. (단, \(n=100\), \(m=10000\))

  • \(n\)개의 샘플 \(x_1, \ldots, x_{n}\)을 추출하여 A방식과 B방식으로 각각 \(\hat\mu_x\)를 계산
  • \(n\)개의 샘플 \(y_1, \ldots, y_{n}\)을 독립적으로 추출하여 A방식과 B방식으로 각각 \(\hat\mu_y\)를 계산
  • 위 과정을 \(m\)번 반복하여 \((\hat\mu_x, \hat\mu_y)\)를 산점도로 표시 (따라서 점은 각 방식별로 \(m\)개씩 있음)
방식 추정량
A (파란색) 표본평균 \(\bar{x}\)
B (주황색) \(\frac{\min(x)+\max(x)}{2}\)

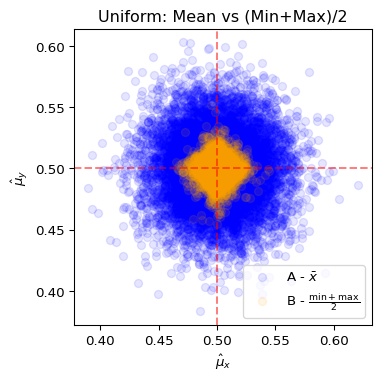
그림에 대한 해석으로 옳은 것을 모두 고르라.

  1. A방식이 MLE에 근거한 추정법이다.
  2. B방식이 MLE에 근거한 추정법이다.
  3. 그림에서는 B방식에 근거한 추정법이 더 우수해 보이는데, 이는 \(n\)이 작아서 생기는 특별한 현상이고, \(n\)이 커진다면 점점 표본평균에 근거한 추정법이 더 우세해진다.
  4. 그림에서는 B방식에 근거한 추정법이 더 우수해보이는데, 이는 표본평균으로 모평균을 추정하는 것이 항상 최선은 아닐수도 있음을 의미한다.

4. 문제 3의 그림에서 주황색 점들의 분포 모양과 파란색 점들의 분포 모양에 대한 설명으로 올바른 것을 모두 고르시오.

  1. 주황색과 파란색 점들의 분포 모양이 다른 이유는 \(n\)이 적기 때문이다.
  2. 주황색 점들이 파란색 점들처럼 원형이 아니라 사각형에 가까운 이유는 \(\min\), \(\max\)에 중심극한정리가 성립하지 않기 때문이다.
  3. \(n\)이 커지면 주황색 점들도 파란색 점들과 같은 모향이 된다.
  4. \(n\)이 커지면 파란색 점들도 주황색 점들과 같은 모향이 된다

5. 피셔(Fisher)의 MLE에 대한 주장으로 틀린 것은?

  1. 분포를 고려하지 않고 무조건 표본평균을 사용하는 것은 최선이 아닐 수 있다.
  2. 정규분포에서 적률법(MME)과 MLE가 일치하는 것은 우연이다.
  3. 균등분포에서 표본평균이 중심의 MLE이다.
  4. MLE는 분포의 특성을 고려하여 최적의 추정량을 찾는다.

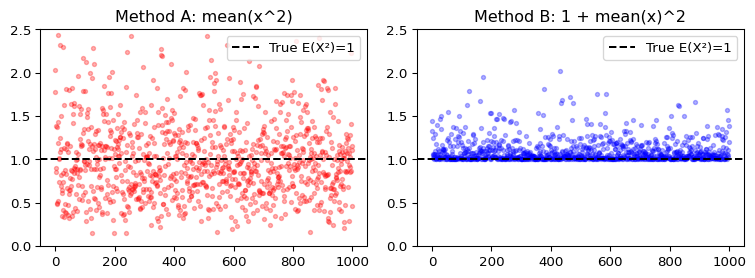
6. \(X \sim N(\mu, 1)\)에서 10개의 샘플을 얻었다. \(\mathbb{E}(X^2)\)를 추정하는 두 방법을 비교한다.

  • A방식: \(\overline{x^2}\) (표본 제곱의 평균)
  • B방식: \(1 + \bar{x}^2\)

그림6: 제곱의 평균에 대한 추정의 비교

방법 A와 B중 MLE에 근거한 방식이 무엇인가? (이유도 쓸 것) MLE에 근거한 방식과 그렇지 않은 방식에 대하여 추정의 효율을 비교하라.

7. 균등분포 \(U(a,b)\)의 가능도함수는 다음과 같다: \[L(a,b)=\frac{1}{(b-a)^n} \times I(a \leq \min(data)) \times I(\max(data) \leq b)\]

이 가능도함수에 대한 설명으로 틀린 것은?

  1. \(a > \min(data)\)이면 가능도는 0이다
  2. \(b < \max(data)\)이면 가능도는 0이다
  3. \((b-a)\)가 클수록 가능도가 커진다
  4. \(a=\min(data)\), \(b=\max(data)\)일 때 가능도가 최대이다