12wk-1: 최대가능도추정 (4)

최규빈

2025-11-17

강의영상

{{}}

MLE 불변성(Invariance)

예제1

공평한 동전을 5회 던져서 아래와 같은 결과를 얻었다고 하자.

\(0, 1, 0, 0, 1\)

실패확률을 추정하라.

(풀이) – MLE에 기초한풀이

\(X_1,X_2,\dots,X_n \sim Ber(\theta)\) 에서 MLE에 의한 \(\theta\)의 추정값은 \(\frac{2}{5}\)이므로 (왜?) 성공확률 \(\theta\)는 \(\frac{2}{5}\)로 추정할 수 있다. 실패할확률은 \(1-\theta\)인데, \(\theta\)의 값을 이미 \(\frac{2}{5}\)로 추정했으므로 실패할확률의 추정값은 \(1-\frac{2}{5}=\frac{3}{5}\)이라고 할 수 있다.

- 개념: MLE에 기반한 추정법은 아래와 같다.

모수를 MLE로 추정한다
추정의 대상과 모수와의 함수관계를 파악한다.
1에서 얻은 추정값을 2에서 얻은 함수관계에 대입한다.

- 이 논리로 위의 예제를 다시 해석하면 아래와 같다.

모수를 추정한다: 베르누이 분포 \(Ber(\theta)\)의 모수는 성공확률 \(\theta\)이며, \(\theta\)의 추정값은 \(\frac{2}{5}\) 이다.
추정의 대상과 모수와의 함수관계를 파악한다: 추정의 대상은 실패확률이다. 그런데 “\(실패확률=1-\theta\)”라는 관계가 있는데 이것이 추정의 대상과 모수와의 함수관계이다.
1에서 얻은 추정값을 2에서 얻은 함수관계에 대입한다: 우리가 1에서 얻은 추정값은 \(\frac{2}{5}\)이다. 2에서 얻은 함수관계는 \[추정의대상=실패확률=1-\theta\]이다. 1에서 얻은 \(\theta\)에 대한 추정값 \(\frac{2}{5}\)를 위의 \(\theta\)자리에 plugin하면 \(실패확률=\frac{3}{5}\)를 얻는다.

- 주의(고급내용): 3의 과정을 수식으로 표현하면 아래와 같다.

\[\widehat{실패확률}^{MLE}=\widehat{1-\theta}^{MLE}=1-\hat{\theta}^{MLE}\]

이러한 논리전개는 언뜻 당연해보이지만 사실 당연한건 아니다. 아래와 같은 사실은

\[\widehat{1-\theta}^{MLE}=1-\hat{\theta}^{MLE}\]

일반적인 추정법에는 성립하지 않는다. 오직 MLE에서만 이러한 논리전개가 가능함. (MLE가 가진 좋은 성질임)

예제2

아래에서

\[X \sim N(\mu,1)\]

얻은 10개의 샘플이 다음과 같다고 하자.

 [1] -0.56047565 -0.23017749  1.55870831  0.07050839  0.12928774  1.71506499
 [7]  0.46091621 -1.26506123 -0.68685285 -0.44566197

\(\mathbb{E}(X^2)\)을 추정하라.

(참고)

진실세계의정보: \(\mathbb{E}(X), \mathbb{E}(X^2)\)
데이터세계의정보: \(\bar{x}\)

(풀이)

언뜻 생각하면 아래와 같이 추정해야 할 것 같다.

mean(x^2)

[1] 0.8243026

그런데 \[\mathbb{E}(X^2)=\big\{\mathbb{E}(X)\big\}^2+\mathbb{V}(X)\]

임을 고려하면 아래와 같이 추정하는것도 말이 되는 것 같다.

mean(x)^2 + 1

[1] 1.005569

두 값은 얼추 비슷하지만 완전히 같지는 않다. 둘다 타당한 추정법인것 같은데 무엇이 더 올바른 추정일까?

분석

A <- c()
B <- c()
for(i in 1:1000){
    x <- rnorm(10)
    A[i] <- mean(x^2)
    B[i] <- 1+mean(x)^2
}
plot(A,col='red',xlab="",ylab="")
points(B,col='blue',xlab="",ylab="")

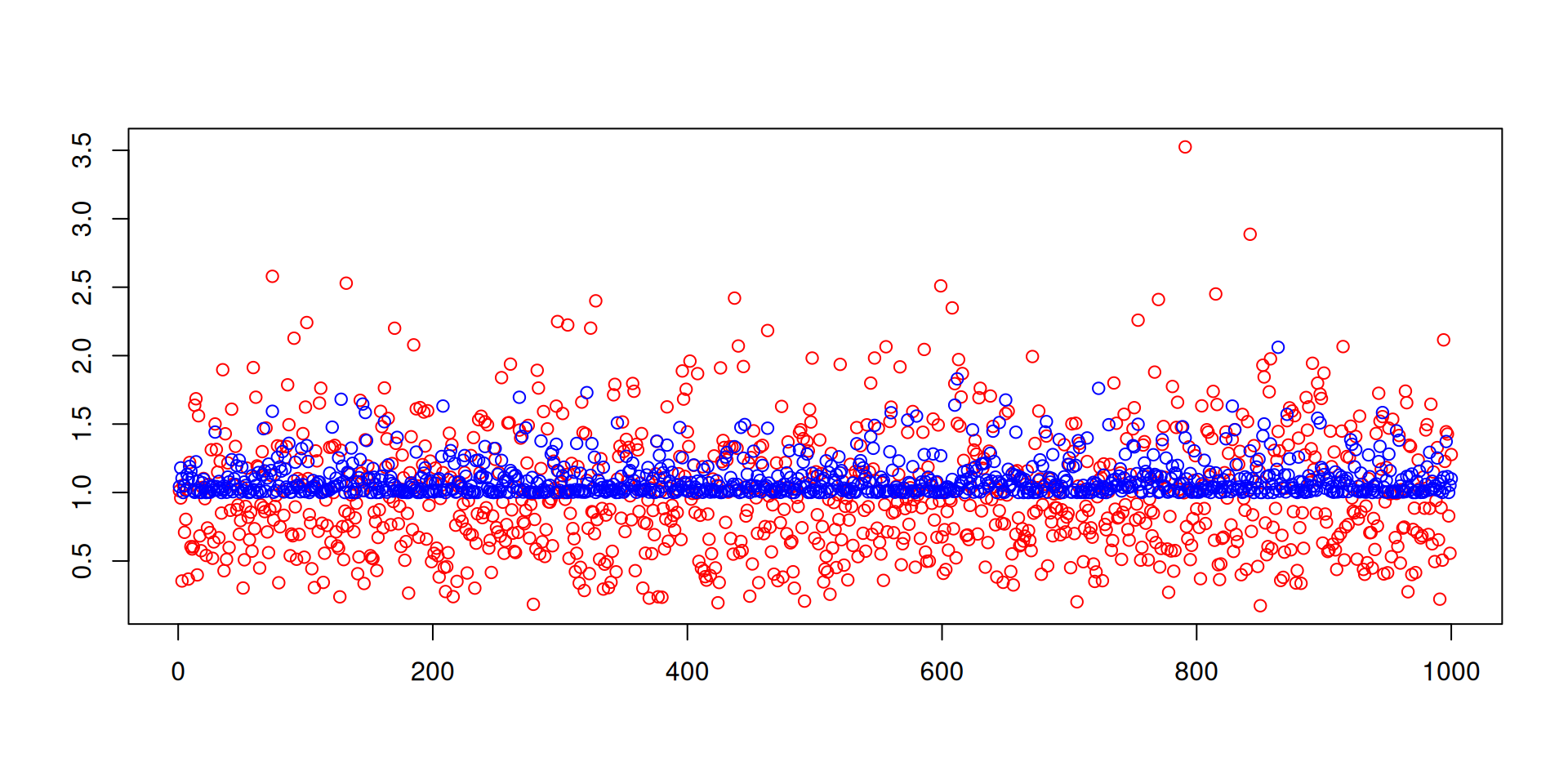
그림1: 추정의비교, 빨간색은 \(\text{mean}(x^2)\), 파란색은 \(1+\text{mean}(x)^2\).

비교한 결과 방법A와 방법B중에서는 방법B가 더 우수하다는 생각이 든다.

방법A: \(\text{mean}(x^2)=\bar{x^2}\)
방법B: \(1+\text{mean}(x)^2=1+\bar{x}^2\)

왜 그럴까? 사실 방법B는 최대가능도방법의 원리로 추정된 값이기 때문이다.

모수를 MLE로 추정한다: 정규분포의 모수는 \(N(\mu,\sigma^2)\)인데, \(\sigma=1\)로 주어졌으므로 추정할 필요가 없고, \(\mu\)를 추정하면 \(\bar{x}\)이다.
추정의 대상과 모수와의 함수관계를 파악한다: \(\mathbb{V}(X)=\mathbb{E}(X^2)-\{\mathbb{E}(X)\}^2\)의 관계가 있으므로 추정의 대상은 \(\mathbb{E}(X^2)=\sigma^2+\mu^2\)와 같이 표현할 수 있음. 그런데 \(\sigma^2=1\)이 주어졌으므로 “\(추정의대상=\mathbb{E}(X^2)=1+\mu^2\)” 의 관계가 있음.
1에서 얻은 추정값을 2에서 얻은 함수관계에 대입한다: 따라서 \[{\mathbb{E}(X^2)}의 추정값 = 1+\bar{x}^2\]

균등분포

구간 \((a,b)\)에서 임의의 난수를 뽑는 실험을 상상하자. 이러한 실험은 아래와 같이 표현할 수 있다. \[X \sim U(a,b)\]

여기에서 \(U\)는 uniform의 약자이다. 히스토그램을 그려보자. (이때 \(a=1, b=2\)를 가정함)

그림2: 균등분포의 히스토그램

히스토그램의 극한을 상상하고 pdf의 수식을 쓰면 아래와 같다.

\[f_X(x)=\frac{1}{b-a}, \quad a \leq x \leq b\]

수식을 좀 더 정리하면 아래와 같다.

\[f_X(x)=\frac{1}{b-a}I(a \leq x \leq b)\]

여기에서 \(I(a \leq x \leq b)=\begin{cases} 1 & a \leq x \leq b \\ 0 & o.w. \end{cases}\) 이다. 이제 아래와 같은 관측치를 얻은 상황에서 x의 중심 \(\mathbb{E}(X)\)를 추정하는 문제를 고려하자.

set.seed(123)
x <- runif(n=10, min=1,max=2)
x

 [1] 1.287578 1.788305 1.408977 1.883017 1.940467 1.045556 1.528105 1.892419
 [9] 1.551435 1.456615

(1) 가능도함수를 구하라.

(풀이)

가능도함수의 수식은 아래와 같다. \[L(\theta|data)=f(data|\theta)\]

여기에서 \(\theta = (a,b)\) 이다. 그런데

\(f(data|\theta) = f(x_1,\dots,x_{10}|\theta)=f(x_1|\theta)\dots f(x_{10}|\theta)\)
\(f(x_1|\theta) = \frac{1}{b-a}I(a\leq x_1 \leq b)=\frac{1}{b-a}I(a\leq x_1)I(x_1\leq b)\)

이므로 가능도 함수는 아래와 같다.

\[L(a,b)=\frac{1}{(b-a)^{10}}\times I(a\leq x_1)\dots I(a \leq x_n)\times I(x_1\leq b)\dots I(x_n\leq b)\]

가능도 함수를 정의하기전에

a=1.2
b=1.5

주어진 \(a,b\)에 대한 아래의 값들을 조사하여보자.

print((b-a)^10)

[1] 5.9049e-06

print(x)

 [1] 1.287578 1.788305 1.408977 1.883017 1.940467 1.045556 1.528105 1.892419
 [9] 1.551435 1.456615

print(a<=x)

 [1]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE

print(x<=b)

 [1]  TRUE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE

가능도함수는 아래와 같이 정의된다.

likelihood = 1/(b-a)^10 * prod(a<=x) * prod(x<=b)
likelihood

[1] 0

(2) 가능도함수의 특징을 살펴보자.

(풀이)

가능도함수는 항상 양수임
가능도가 0이 안나올라면 \(a\)는 \(1.045556\)보다 작아야하고, \(b\)는 \(1.940467\)보다 커야함.

(3) 가능도함수의 값을 표로 정리하자.

(풀이)

\(L(a,b)\)에 대한 값을 조사하여 표를 만들어보면 아래와 같다.

	\(b=1.5\)	\(b=1.8\)	\(b=2.1\)	\(b=2.4\)	\(b=2.7\)	\(b=3\)
\(a=0\)	0.00e+00	0.00e+00	6.00e-04	1.58e-04	4.86e-05	1.69e-05
\(a=0.3\)	0.00e+00	0.00e+00	2.80e-03	6.00e-04	1.58e-04	4.86e-05
\(a=0.6\)	0.00e+00	0.00e+00	1.73e-02	2.80e-03	6.00e-04	1.58e-04
\(a=0.9\)	0.00e+00	0.00e+00	1.62e-01	1.73e-02	2.80e-03	6.00e-04
\(a=1.2\)	0.00e+00	0.00e+00	0.00e+00	0.00e+00	0.00e+00	0.00e+00
\(a=1.5\)	0.00e+00	0.00e+00	0.00e+00	0.00e+00	0.00e+00	0.00e+00

표를보면 \((a,b)=(0.9, 2.1)\)에서 최대값을 가지는 듯 하다.

(4) 가능도함의 그림을 그려보자.

(풀이)

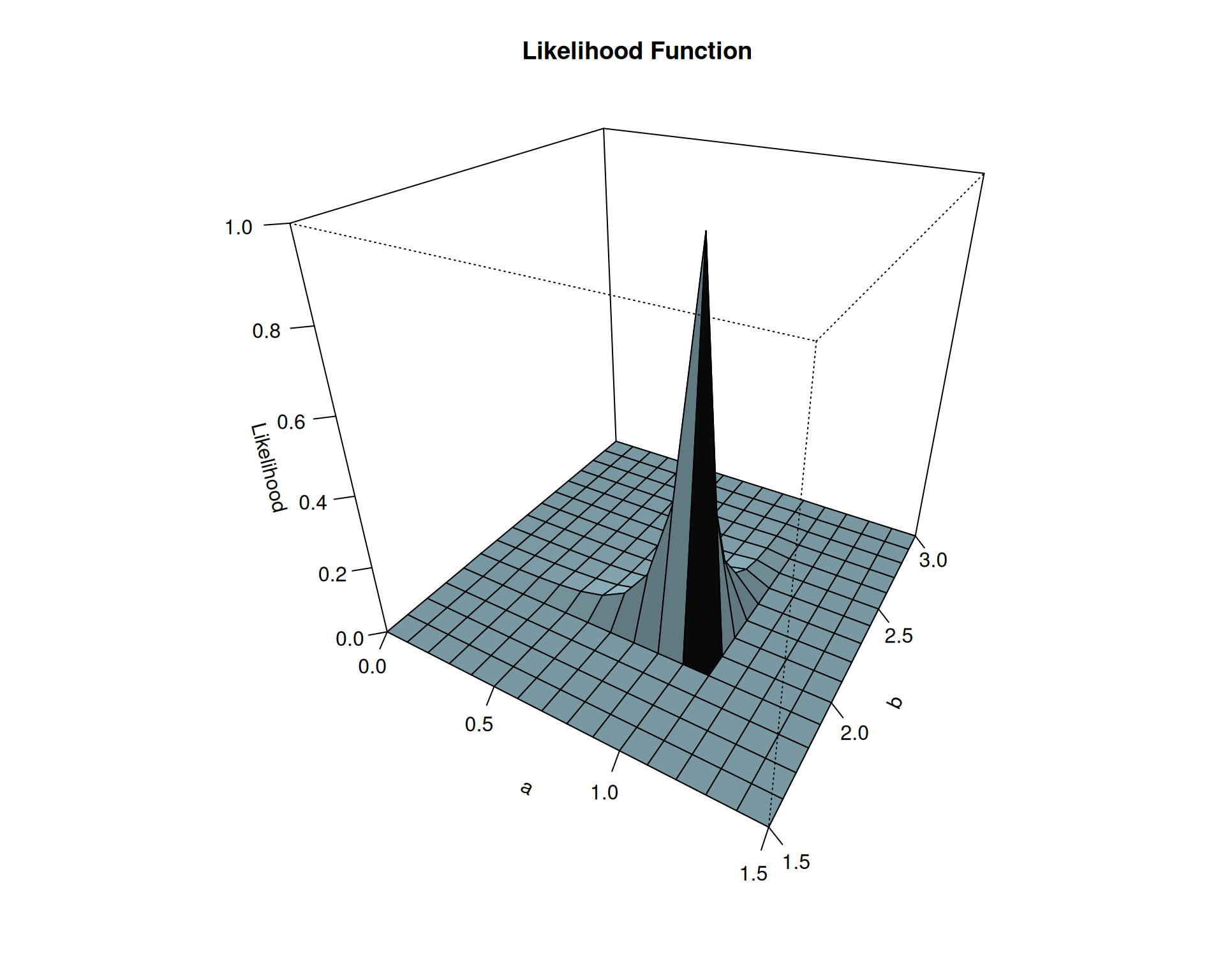
그림3: \(a\), \(b\)에 대한 likelihood 함수의 3D plot

\((a,b)=(1.1,1.9)\) 에서 최대값을 가지는 것 같다.

(5) 이론적인 MLE를 구하라.

(풀이)

가능도함수의 수식은 아래와 같다. \[L(a,b)=\frac{1}{(b-a)^{10}}\times I(a\leq x_1)\dots I(a \leq x_n)\times I(x_1\leq b)\dots I(x_n\leq b)\]

그런데

\(I(a\leq x_1)\dots I(a \leq x_n) = I(a \leq \min(x_1,\dots,x_n))\)
\(I(x_1\leq b)\dots I(x_n\leq b)= I(\max(x_1,\dots,x_n)\leq b)\)

이고

print(min(x)); print(max(x))

[1] 1.045556

[1] 1.940467

이므로

\(I(a\leq x_1)\dots I(a \leq x_n) = I(a \leq \min(x_1,\dots,x_n))=I(a\leq 1.045556)\)
\(I(x_1\leq b)\dots I(x_n\leq b)= I(\max(x_1,\dots,x_n)\leq b)=I(1.940467 \leq b)\)

와 같이 정리된다. 따라서 가능도함수는 아래와 같다.

\[L(a,b)=\frac{1}{(b-a)^{10}}\times I(a\leq 1.045556)\times I(1.940467 \leq b)\]

수식을 살펴보면 (1) \(a\leq 1.045556\) 이고 \(b\geq 1.940467\)일 경우만 가능도함수는 \(0\)이 아닌 값을 가지고 (2) 그 값은 \((b-a)\)값이 작을수록 최대가 되므로 \[(a,b)=(1.045556,1.940467)\]에서 이론적인 최대값을 가진다.

이 결과는 일반화될 수 있으므로 아래와 같이 정리가능하다.

\(X_1,\dots,X_n \overset{iid}{\sim} U(a,b)\) 일때 가능도함수는 아래와 같고 \[L(a,b)=\frac{1}{(b-a)^n}\times I(a \leq \min(data)) \times I(\max(data)\leq b)\] \(a,b\)를 최대가능도추정법으로 추정하면 각각 아래와 같다.

\(a의 추정값 = \min(data)\)

\(b의 추정값 = \max(data)\)

(6) \(\mathbb{E}(X)\)의 값을 추정하라. (최대가능도추정법을 사용할 것)

(풀이)

아래를 다시 따르면 된다.

모수를 MLE로 추정한다.
추정의 대상과 모수와의 함수관계를 파악한다.
1에서 얻은 추정값을 2에서 얻은 함수관계에 대입한다.

1. 균등분포의 모수는 \(a,b\)이고 이를 각각 추정한 결과는 \(\min(data)\), \(\max(data)\)이다.

2. 추정의대상은 \(X\)의 평균인데 이 값은 (직관적으로) \[\mathbb{E}(X)=\frac{a+b}{2}\] 와 같이 계산할 수 있다.

3. 따라서 평균의 추정값은 \(\frac{\min(data)+\max(data)}{2}\)로 계산할 수 있다.

이제 11wk-2의 예제3(마지막 예제)의 결과를 다시 살펴보자. 왜 중심을 추론할때 양 극단값만 고려하면 충분한지 이해가 되는가?

- 결론

MLE는 데이터분석에서 가장 유용한 추정방법이라 할 수는 없지만 (사람마다 취향이 있으니까요?)
꽤 유용하고 많은 분야에서 의미있게 사용된다.
특히 기존에 사용되었던 MME (평균으로 해결하자는 주의) 와 비교해서는 성능이 좋다고 알려져있다.¹