10wk-1: 확률과 가능도 (Python, 참고자료)

Author

최규빈

Published

November 5, 2025

강의영상

  • 본 강의노트로는 강의를 하지 않음.

복습: 피셔의 문제의식

피셔는 1922년 그의 논문 “On the Mathematical Foundations of Theoretical Statistics”에서 혼란이 발생하는 원인을 아래와 같이 주장하였다.

  1. 용어가 불분명해서 그렇다. (즉 순전히 언어적인 혼란이다)
  2. “확률”이라는 개념을 너무 남발해서 그렇다. (역확률)

확률과 가능도

# 예제1

앞면이 나오는 확률을 알 수 없는 동전을 2번 던져서 아래와 같은 결과를 얻었다고 하자.

  • \(x_1=0\)
  • \(x_2=1\)

앞면이 나오는 확률이 0.5였다고 생각하는 것이 타당한가? 아니면 앞면이 나오는 확률이 0.1이었다고 생각하는 것이 타당한가?

(풀이)

\(x_1=0,x_2=1\)는 \(Ber(\theta)\)에서 얻은 실현치라고 가정하자. 만약에 \(\theta=0.5\)였다면 이러한 실현치를 얻을 확률은 아래와 같다.

0.5*0.5
0.25

만약에 \(\theta=0.1\)이었다면 이러한 실현치를 얻을 확률은 아래와 같다.

0.9*0.1
0.09000000000000001

\(0.25>0.09\) 이므로 \(\theta=0.5\)라고 생각하는 것이 더 타당해보인다.

질문: \(0.25\)를 \(\theta=0.5\)일 확률, \(0.09\)를 \(\theta=0.1\)일 확률로 해석하는건 어떨까? 타당한 용어일까?

퀴즈

1. \(x_1=0\), \(x_2=1\)은 진실세계의 정보인가? 아니면 데이터세계의 정보인가?

2. \(\bar{x}=\frac{x_1+x_2}{2}=0.5\)를 표현할 수 있는 용어는 (1) 표본평균 (2) 모평균 (3) 평균

3. 문제를 보고 \(X_1,X_2 \overset{iid}{\sim} Ber(\theta)\)를 떠올렸다. 이러한 과정을 무엇이라고 하는가?

4. \(\theta\)를 표현할 수 있는 용어는? (a) 모평균 (b) 표본평균 (c) 평균 (d) 모수

5. \(x_1,x_2\)의 값을 바탕으로 \(\theta\)의 구체적인 값을 산정하는 과정을 무엇이라고 하나? (a) 추정 (b) 모수추정 (c) 모평균의 추정

#

# 예제2 – 예제1과 같은상황

앞면이 나오는 확률을 알 수 없는 동전을 2번 던져서 아래와 같은 결과를 얻었다고 하자.

  • \(x_1=0\)
  • \(x_2=1\)

아래와 같은 용어가 성립가능할까?

  • \(P(\theta=0.5)=0.5 \times 0.5 = 0.25\)
  • \(P(\theta=0.1)=0.1 \times 0.9 = 0.09\)

(풀이1)

성립한다고 치자. 그렇다면 아래와 같은 확률들도 정의할 수 있어야 한다.

  • \(P(\theta=0.51)\), \(P(\theta=0.52)\), \(P(\theta=0.53)\), \(P(\theta=0.54)\), \(\dots\)
  • \(P(\theta=0.49)\), \(P(\theta=0.48)\), \(P(\theta=0.47)\), \(P(\theta=0.46)\), \(\dots\)
print(0.51*0.49); print(0.52*0.48); print(0.53*0.47); print(0.54*0.46)
print(0.49*0.51); print(0.48*0.52); print(0.47*0.53); print(0.46*0.54)
0.2499
0.2496
0.2491
0.24840000000000004
0.2499
0.2496
0.2491
0.24840000000000004

저 위의 숫자들을 모두 더하면 아래와 같음.

(0.2499 + 0.2496 + 0.2491 + 0.2484)*2
1.9939999999999998

1이 넘네? (모순)

(피셔의생각1)

진실의 세계에서 데이터의 세계로 넘어갈때만 “확률”이라는 개념이 적용된다. 즉 확률은 반드시 아래와 같은 개념으로만 사용되어야 한다.

\[\text{진실의 세계} \overset{P}{\Longrightarrow} \text{데이터의 세계}\]

즉 우리는 \(\theta=0.5\)를 고정한뒤

\[P(X_1=x_1, X_2=x_2)=P(X_1=0, X_2=1)=0.25\]

라고 쓰는 것은 허용할 수 있지만 \(x_1=0, x_2=1\)을 고정한 뒤

\[P(\theta=0.5)=0.25\]

라고 쓰는 건 용납불가능하다.

(피셔의생각2)

확률은 반복가능한 대상에 대해서만 적용가능하다. 왜냐하면 확률은 상대빈도의 극한이기 때문이다. 예를들어 \(x_1, x_2\)은 반복적으로 관찰가능한 대상이므로 \[P(X_1=x_1, X_2=x_2)\]와 같은 표현은 성립한다. 예를들어 \(P(X_1=0, X_2=1)=0.25\)라는 의미는 아래와 같은 관측을 많이하면 대충 \(x_1=0, x_2=1\)이 나올 상대빈도가 \(0.25\)정도 된다는 뜻이다.

for i in range(10):
    print(np.random.binomial(1, 0.5, 2))
[1 0]
[1 1]
[0 1]
[0 0]
[1 0]
[0 0]
[0 0]
[1 1]
[1 0]
[1 0]

그렇디만 \(P(\theta=0.5)=0.25\)는 다르다. 이는 상대빈도의 극한으로 해석할 수 없다. \(\theta=0.5\)는 추정해야할 대상이지 (진실공간의 정보이지) 반복관측가능한 대상이 아니다 (데이터공간의 정보가 아니다).

빈도주의: 확률은 상대빈도의 극한으로 해석할 때 의미가 있다. \((\star\star\star)\)

#

Notation: \(P(X=x | \theta=\theta_0), f(x|\theta=\theta_0)\)

\(X_1,X_2 \overset{iid}{\sim} Ber(0.5)\) 일때 \(P(X_1=x_1,X_2=x_2)\)는 좀 더 명확하게 아래와 같이 쓸 수 있다.

\[P(X_1=x_1, X_2=x_2 | \theta= 0.5)\]

원래 \(P\)가 \(\theta\)에 의존함을 강조하고 싶을때는 “\(P\)” 대신에 “\(P_{\theta}\)”와 같이 쓰기도 한다고 했잖아요? 그 연장선에서

  1. \(P(X_1=0, X_2=1)\)
  2. \(P_{\theta}(X_1=0, X_2=1)\)

와 같은 표현은 사실 혼용해서 사용합니다. 만약에 \(\theta=0.5\)일 경우는 1은 그대로 \(P(X_1=0, X_2=1)\)로 쓰면되지만 2의 경우는 \(P_{0.5}(X_1=0,X_2=1)\)와 같이 쓰기 좀 어색하죠? 그래서 아래와 같이 사용합니다.

  • \(P_{\theta}(X_1=0, X_2=1)\). 단, \(\theta=0.5\).
  • \(P(X_1=0, X_2=1 | \theta = 0.5)\).

이를 좀 더 일반화하면 아래와 같은 기호약속을 할 수 있다.

# 약속1 – \(X \sim P_{\theta}\) 일때 \(P(X=x|\theta=\theta_0)\)은 모수가 \(\theta_0\) 라고 가정하였을 경우 관측치 \(X=x\)를 얻을 확률을 의미한다.

\(X_1,X_2 \overset{iid}{\sim} Ber(\theta)\) 라고 할때 아래를 풀어보자.

  1. \(P(X_1=0 ~|~ \theta=0.1)\)
  2. \(P(X_1=0,X_2=1 ~|~ \theta=0.2)\)
  3. \(P(X_1=0,X_2=1 ~|~ \theta=0.3)\)
  4. \(P(X_1=0,X_2=1 ~|~ \theta=0.4)\)
  5. \(P(X_1=1,X_2=0 ~|~ \theta=0.4)\)
  6. \(P(X_1+X_2=0 ~|~ \theta=0.5)\)
  7. \(P(X_1+X_2\geq 0 ~|~ \theta=0.5)\)
  8. \(P(\max(X_1,X_2)=1 ~|~ \theta=0.5)\)
  9. \(P(\bar{X}=\frac{1}{2} ~|~ \theta=0.5)\)

# 약속2 – 연속확률변수 \(X\)의 확률밀도함수가 \(f_X\)라고 하자. \(f_X(x|\theta=\theta_0)\)이라는 의미는 모수가 \(\theta_0\)이라고 가정하였을 경우 \(x\)에서의 확률밀도함수값을 의미한다.

\(X \sim N(\mu,\sigma^2)\) 라고 할때 아래를 풀어보자. (힌트: 정규분포의 pdf는 \(f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)임.)

  1. \(f_X(0 | \mu=0, \sigma=1)\)
  2. \(f_X(0 | \mu=1, \sigma=1)\)
  3. \(f_X(0 | \mu=0, \sigma=2)\)

(풀이)

손으로는 못푸니까 계산기를 이용합시다.

# 1번
mu=0; sigma=1; x=0; print(1/(sigma*np.sqrt(2*np.pi))*np.exp(-(x-mu)**2/(2*sigma**2)))
# 2번
mu=1; sigma=1; x=0; print(1/(sigma*np.sqrt(2*np.pi))*np.exp(-(x-mu)**2/(2*sigma**2)))
# 3번
mu=0; sigma=2; x=0; print(1/(sigma*np.sqrt(2*np.pi))*np.exp(-(x-mu)**2/(2*sigma**2)))
0.3989422804014327
0.24197072451914337
0.19947114020071635

Note: 1-2, 1-3간의 크기비교는 계산기를 가지고 있지 않아도 할 수 있습니다.

가능도

\(X_1,X_2 \overset{iid}{\sim} Ber(\theta)\) 에서 관측한 관측치가 \(x_1=0, x_2=1\) 이라고 하자.

  • \(\theta=0.5\)라면 이러한 관측치를 얻을 확률이 \(0.25\)이고
  • \(\theta=0.1\)라면 이러한 관측치를 얻을 확률이 \(0.09\)이다.

그렇지만 이것이

  • \(\theta=0.5\)일 확률이 \(0.25\)이고
  • \(\theta=0.1\)일 확률이 \(0.09\)이라는

의미는 아니다.

사실 “\(\theta=0.5\)라면 이러한 관측치를 얻을 확률이 \(0.25\)”라는 표현은 정확하긴 하지만 길고 복잡하다. 그래서 적당한 용어 OOO를 정의해서

  • \(\theta=0.5\)일 OOO가 \(0.25\)이고
  • \(\theta=0.1\)일 OOO가 \(0.09\)이고

와 같이 표현하고 싶다. 여기에서 OOO에 해당하는 용어가 “가능도(likelihood)”이다. 가능도의 일반적인 정의는 아래와 같다.

정의1 – 가능도와 가능도함수

가능도 \(L(\theta|x)\)는 관측된 데이터 \(x\)가 주어졌을 때, 모수 \(\theta\)의 그럴듯한 정도를 수치화 하여 측정한 것으로, 다음과 같이 정의된다:

  • 이산형 확률변수: \(L(\theta|x) = P(X=x|\theta)\)
  • 연속형 확률변수: \(L(\theta|x) = f_X(x|\theta)\)

여기에서 \(L(\theta|x)\)는 간단히 \(L(\theta)\)라고 표현하기도 하며 이를 \(\theta\)에 대한 가능도함수라고 한다.

가능도라는 용어에 익숙해지기 위해서 아래의 문제를 풀어보자.

\(X_1,X_2 \overset{iid}{\sim} Ber(\theta)\) 라고 하자.

  1. \(L(0.5 | x_1=0, x_2=1)=???\)
  2. \(L(0.3 | x_1=0, x_2=1)=???\)
  3. \(L(0.5 | x_1+x_2=1)=???\)
  4. \(L(0.5 | \bar{x}=0.5)=???\)
  5. \(L(0.5 | \bar{x}=0.4)=???\)
  6. \(L(0.5 | \bar{x}=0)=???\)
  7. \(L(\theta | \bar{x}=0.5)=???\)
  8. \(L(\theta | \bar{x}=0.4)=???\)
  9. \(L(\theta | \bar{x}=0)=???\)

가능도와 확률의 차이

  1. 총합이 1이라는 보장이 없다.1
  2. 서로소인 집합 \(A,B\)에 대한 확률의 공리 \[P(A \cup B)=P(A)+P(B)\]가 성립하지 않는다. (가능도는 점 단위로만 정의가능하다)

\(X_1,X_2 \overset{iid}{\sim} Ber(\theta)\) 에서 관측치 \(x_1=0, x_2=1\)을 얻었다고 하자. 아래와 같은 표현은 불가능하다.

  • \(L(\theta \in \{0.5, 0.49\}) = L(0.5) + L(0.49)\)
  • \(L(\theta \in [0,1]) > L(0.5)\)
  • \(L(\theta < 0) = 0\)

그 예제

08wk-1 예제 – 아래를 관찰하자.

그림2: 3000개의 점으로 구성된 산점도

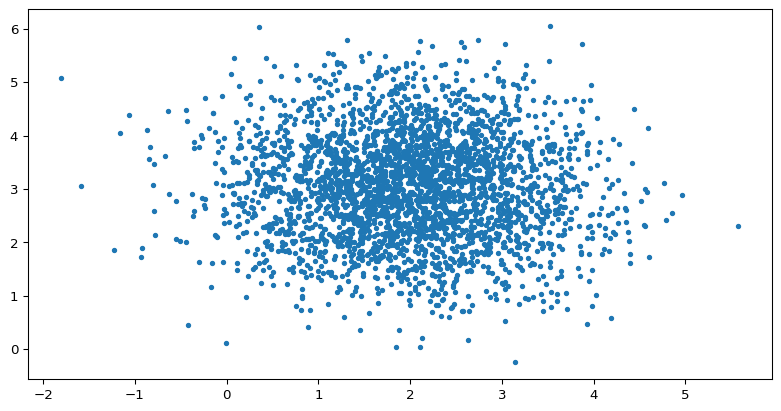
다음 중 그림을 아래와 같이 묘사했다고 하자. (\(\sigma_x=\sigma_y=1\)로 알려져있다고 가정하자.)

  1. \(x\)축의 평균은 2이다.
  2. \(y\)축의 평균은 3이다.
  3. 평균은 \((2,3)\)이다.
  4. 평균은 어딘가에 있다. 즉 평균은 \((x_0,y_0)\) 인데 \(x_0 \in \mathbb{R}, y_0 \in \mathbb{R}\).

이는 아래와 같이 서술한것과 같다.

  1. \(L(\mu_x=2,\mu_y \in \mathbb{R})\)
  2. \(L(\mu_x\in \mathbb{R} ,\mu_y=3)\)
  3. \(L(\mu_x=2,\mu_y=3)\)
  4. \(L(\mu_x\in \mathbb{R} ,\mu_y \in \mathbb{R})\)

Footnotes

  1. \(\int L(\theta|x) d\theta \neq 1\)↩︎