08wk-1: 진실의 세계와 데이터의 세계 (Python, 참고자료)

Author

최규빈

Published

October 21, 2025

강의영상

본 강의노트로는 강의를 하지 않음.

도입

예제1 – 엑스노트

reference: 201x년 김용대 교수님 수업을 들으며 착안한 예제..

앞의 그림을 가장 적절히 설명한 진술이 무엇이라고 생각하는가?

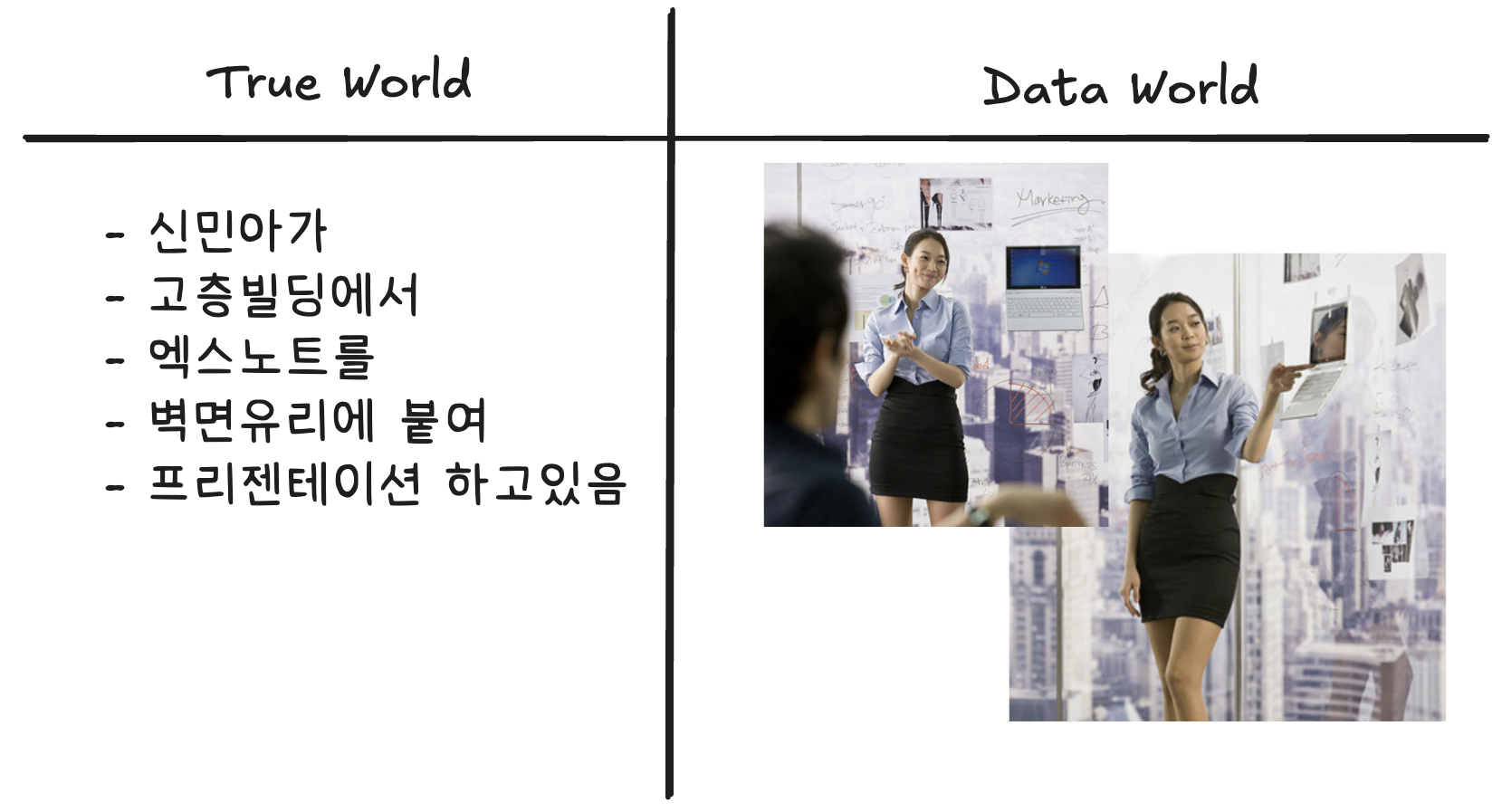
신민아가 고층빌딩에서 엑스노트를 벽면유리에 테잎을 붙여 프리젠테이션을 하고 있다.
젋은여성이 노트북을 활용하여 프리젠테이션을 하고 있다.
여성이 프리젠테이션을 하고 있다.

이제 아래의 진술이 맞을 “확률”을 생각해보자. 1,2,3중에 어떠한 문장이 참일 확률이 가장 높은가?

신민아가 고층빌딩에서 엑스노트를 활용해 프리젠테이션을 하고 있다.
젋은여성이 노트북을 활용하여 프리젠테이션을 하고 있다.
여성이 프리젠테이션을 하고 있다.

예제2 – 아래의 그림을 관찰하자.

다음 중 그림을 가장 잘 묘사한 것은?

\(x\)축의 평균은 2이다.
\(y\)축의 평균은 3이다.
평균은 \((2,3)\)이다.
평균은 어딘가에 있다. 즉 평균은 \((x_0,y_0)\) 인데 \(x_0 \in \mathbb{R}, y_0 \in \mathbb{R}\).

진술 1-4가 맞을 확률은?

왜 이러한 혼란이 생기는가? 피셔는 1922년 그의 논문 “On the Mathematical Foundations of Theoretical Statistics”에서 혼란이 발생하는 원인을 아래와 같이 주장하였다.

용어가 불분명해서 그렇다. (즉 순전히 언어적인 혼란이다)
“확률”이라는 개념을 너무 남발해서 그렇다. (역확률)

모수 vs 추정치

용어가 불분명하다는 것이 무슨 의미일까?

예제1 – 애매한 언어

질문1: 공평한 동전을 던진다고 가정하자. 동전을 던저서 나오는 앞면이 나오면 \(X=0\)이라고 하고 뒷면이 나오면 \(X=1\)이라고 하자. \(X\)의 평균은 얼마인가?
질문2: 동전을 5번 던져서 \((0,1,0,0,1)\)을 얻었다고 하자. 평균이 얼마인가?

- 사람들은 알고 싶지만 오직 추정만 할 수 있는 참값(모수)과 추정 방법을 통해 도출된 값(추정치) 모두에 대해 같은 이름을 사용하는 관습이 있다.

구분	진실의 세계	데이터의 세계
성격	알고 싶지만 오직 추정만 할 수 있는 참값 (true value)	추정 방법을 통해 도출된 특정 값 (particular value at which we happen to arrive)
용어	모수 (parameter)	추정치 (estimate)
평균	모평균 \(\mu\)	표본평균 \(\bar{x}\)
표준편차	모표준편차 \(\sigma\)	표본표준편차 \(s\)

고등학교 과정 복습

- 베르누이 시행 (Bernoulli Trial)

결과가 “성공(1)” 또는 “실패(0)” 두 가지만 나오는 실험
성공 확률을 \(p\)라고 하면, 실패 확률은 \(1-p\)
예: 동전 던지기 (앞면=성공, 뒷면=실패), 제품 검사 (양품=성공, 불량품=실패)

- 확률변수 (Random Variable)

확률 실험의 결과를 숫자로 대응시키는 함수
베르누이 시행에서: \(X = 1\) (성공), \(X = 0\) (실패)
확률변수 \(X\)가 베르누이 분포를 따른다는 표기: \(X \sim \text{Bernoulli}(p)\) 또는 \(X \sim B(p)\)

- 독립 (Independence)

두 확률변수 \(X_1, X_2\)가 독립: 한 변수의 결과가 다른 변수에 영향을 주지 않음
수학적 정의: \(P(X_1=x_1, X_2=x_2) = P(X_1=x_1) \cdot P(X_2=x_2)\)
예: 첫 번째 동전 던지기 결과가 두 번째 동전 던지기에 영향을 주지 않음

- i.i.d. (independent and identically distributed)

독립 (independent): 확률변수들이 서로 독립
동일한 분포 (identically distributed): 모든 확률변수가 같은 분포를 따름
표기: \(X_1, X_2, \ldots, X_n \overset{iid}{\sim} \text{Bernoulli}(p)\)
의미: \(n\)개의 확률변수가 모두 베르누이\((p)\)를 따르며, 서로 독립적임

- 모평균 (Population Mean)

확률변수 \(X\)의 기댓값 (expected value)
표기: \(\mu = \mathbb{E}[X]\)
의미: 진실의 세계에서 이론적으로 계산되는 평균값
베르누이 분포의 경우: \(\mu = \mathbb{E}(X) = p\)

- 실현치 (Realization) – data

확률변수를 (실험 혹은 시뮬레이션을 통해) 관측하여 얻은 구체적인 실제값
표기: \(x_1, x_2, \dots, x_n\) (소문자)
예: 동전을 5번 던져서 \((0,1,0,0,1)\)을 얻음

- 표본평균 (Sample Mean)

관측치들의 산술평균
표기: \(\bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i\) (소문자)
의미: 데이터의 세계에서 실제로 계산되는 평균값
예: \((0,1,0,0,1)\)의 표본평균은 \(\bar{x} = \frac{0+1+0+0+1}{5} = 0.4\)

예제1 – 명확한 언어

질문1: \(p=0.5\)인 베르누이 시행을 상상하자.¹ \(X\sim B(p)\) 일때 모평균 \(\mathbb{E}(X)\)는 얼마인가?²
질문2: \(X_1,\dots,X_5 \overset{i.i.d.}{\sim}B(0.5)\)의 관측값이 \[(x_1,x_2,x_3,x_4,x_5)=(0,1,0,0,1)\]일때 표본평균 \(\bar{x}=\frac{1}{5}\sum_{i=1}^{5}x_i\)는 얼마인가?

예제2 – 애매한 언어

평균이 0이고 표준편차가 1이 정규분포가 있다고 하자. 아래는 이러한 정규분포에 10개의 data를 뽑은 결과이다.

np.random.seed(123)
x = np.random.normal(size=10)
x

array([-1.0856306 ,  0.99734545,  0.2829785 , -1.50629471, -0.57860025,
        1.65143654, -2.42667924, -0.42891263,  1.26593626, -0.8667404 ])

x의 평균은 아래와 같은 코드로 계산한다.

np.mean(x).item()

-0.26951611032632805

x의 표준편차는 아래와 같이 계산한다.

np.std(x).item()

1.236304801499023

만약에 정규분포에서 10개의 데이터가 아니라 더 많은 data를 얻는다면 어떻게 될까?

np.random.seed(123)
x = np.random.normal(size=10000)
np.mean(x).item(), np.std(x).item()

(0.009711892291595955, 0.9981138545901473)

평균은 점점 평균에 가까워 질 것이고, 표준편차는 점점 표준편차에 가까워질 것이다. (뭐라는거야..??)

Note

아래의 표에서 ???의 값을 채워보자.

진실의 세계	데이터의 세계
모평균 \(\mu=???\)	표본평균 \(\bar{x}=???\)
모표준편차 \(\sigma=???\)	표본표준편차 \(s=???\)

예제3 – 베르누이

아래의 상황을 가정하자.

\[X_1,X_2,X_3 \overset{i.i.d.}{\sim} B(0.5)\]

이로부터 데이터를 아래와 같이 얻었다고 하자.

np.random.seed(1234)
x = np.random.binomial(n=1, p=0.5, size=3)

진실세계의 정보	데이터세계의 정보
\(X_1,X_2,X_3 \overset{i.i.d.}{\sim} B(0.5)\)	\(x_1,x_2,x_3 = (0,1,0)\)

예제4 – 이변량 정규분포

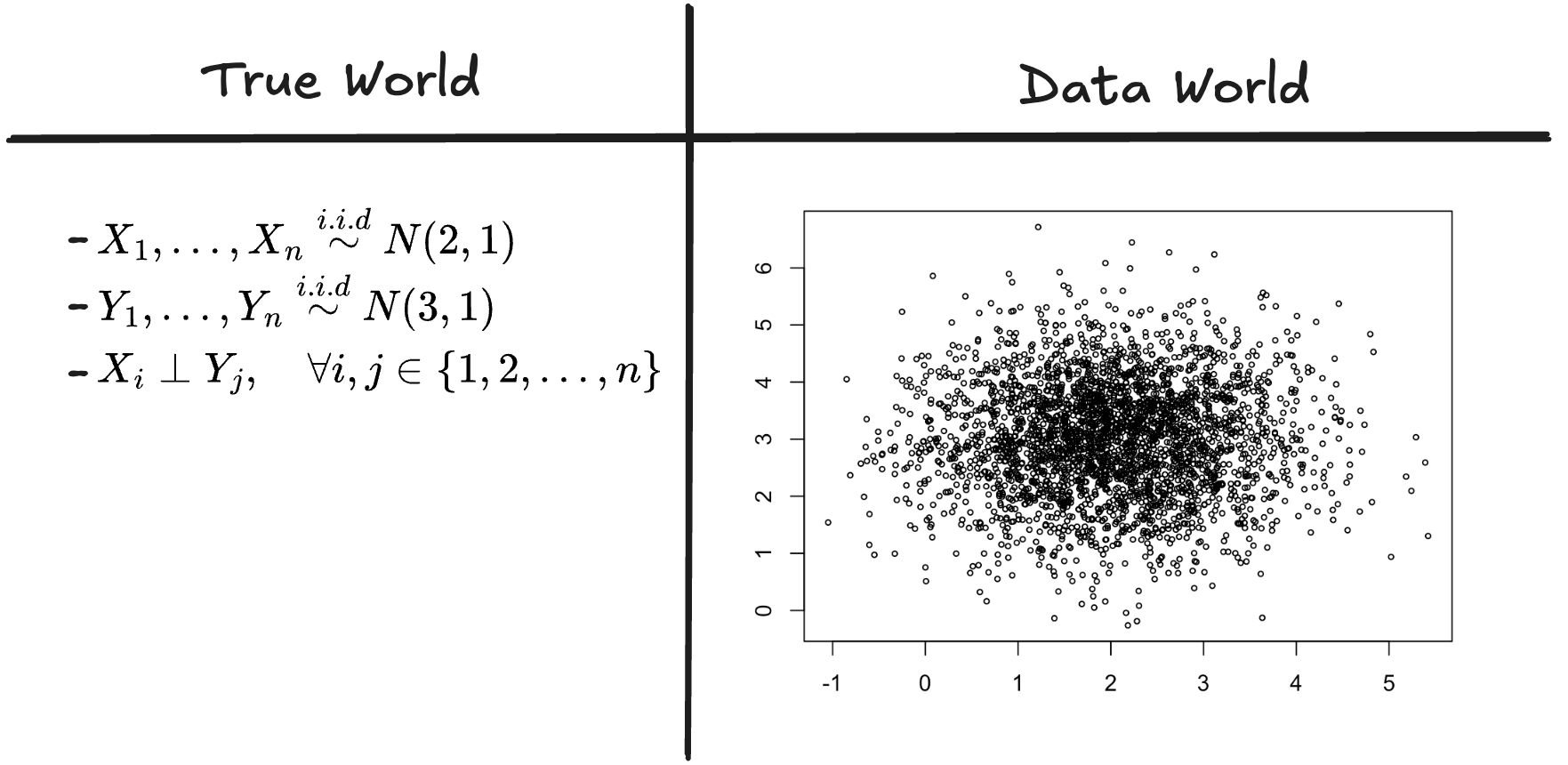
이제 \(n=3000\)에 대해서 아래의 상황을 생각하자.

\(X_1,\dots,X_n \overset{i.i.d}{\sim} N(2,1)\)
\(Y_1,\dots,Y_n \overset{i.i.d}{\sim} N(3,1)\)
\(X_i \perp Y_j,\quad \forall i,j \in \{1,2,\dots,n\}\)

그리고 아래의 코드를 활용하여 데이터를 얻었다.

np.random.seed(123)
x = np.random.normal(loc=2, scale=1, size=3000)
y = np.random.normal(loc=3, scale=1, size=3000)
plt.plot(x, y, '.')

이 경우 진실의 세계와 데이터의 세계는 아래와 같이 생각할 수 있다.

- 통찰1: 진실의 세계에서 데이터의 세계로 넘어가기 위해서는 관측이 필요하다.

- 통찰2: 진실의 세계에서 데이터의 세계로 넘어갈때만 “확률”이라는 개념이 적용된다. 즉 확률은 반드시 아래와 같은 개념으로만 사용되어야 한다.³

\[\text{진실의 세계} \overset{P}{\Longrightarrow} \text{데이터의 세계}\]

- 통찰3: 데이터의 세계는 반복 관찰 가능하다.

예제4 – 동전던지기

진실세계의 정보	데이터세계의 정보
\(X_1,X_2,X_3 \overset{i.i.d.}{\sim} B(0.5)\)	\(x_1,x_2,x_3 = (0,1,0)\)

통찰1: 진실세계의 정보에서 데이터세계의 정보를 얻기 위해서는 반드시 관측이 필요하다.
통찰2: 진실세계의 정보에서 데이터세계의 정보는 확률적으로 얻어진다. (주어진 예시에서는 1/8의 확률로 얻어짐)
통찰3: 데이터세계의 정보는 (관측행위를 되풀이하여) 반복측정 가능하다.
- 예를들어 관측행위를 되풀이하여 \((x_1,x_2,x_3)=(0,0,0)\) 을 얻을수도 있고
- \((x_1,x_2,x_3)=(0,1,1)\) 을 얻을수도 있음.

예제5 – 신민아 배우님..

통찰1: 진실세계의 정보에서 데이터세계의 정보를 얻기 위해서는 관측이 필요
통찰2: 진실세계의 정보에서 데이터세계의 정보는 확률적으로 얻어짐
통찰3: 데이터세계의 정보는 반복측정 가능

Footnotes

공평한 동전을 던진다고 가정하자.↩︎
동전을 던저서 나오는 앞면이 나오면 \(X=0\)이라고 하고 뒷면이 나오면 \(X=1\)이라고 하자. \(X\)의 평균은 얼마인가?↩︎
베이지안 미안해요..↩︎