02wk-2: 카디널리티 (1)

Author

최규빈

Published

September 11, 2025

강의영상

Size와 Cardinality

- 집합 \(A\)의 cardinality는 집합에 들어있는 “원소의 수”를 좀 더 일반화한 개념이다. 집합 \(A\)가 유한집합일 경우는 우리에게 익숙한 size의 개념을 그대로 사용하면 된다. 예를들어 집합 \(A = \{2,3,4\}\) 일 경우는

\[\text{cardinal number of } A := |A| = 3\]

와 같이 사용하면된다. 만약에 집합 \(A\)가 무한집합이라면 그 동작원리가 조금 복잡하다.

- 오늘의 목표: 집합의 size개념을 일반화하자! (그래서 카디널리티라는 개념을 만들자)

  • 익숙한 개념: 두 집합 \(A\),\(B\)의 size 비교 (단, \(A\)와 \(B\)는 유한집합)
  • 파생되는 성질: 두 집합 \(A\), \(B\)사이에 전사, 단사, 전단사 함수가 존재할때 size 비교?
  • 개념의 확장: 두 집합 \(A\),\(B\)의 cardinality 비교 (이때 \(A\)와 \(B\)는 무한집합일수도있음)

전사/단사/전단사

- 용어 정리

  • injective = one-to-one = 단사 = 일대일 함수
  • surjective = onto = 전사 = 위로의 함수
  • bijective = one-to-one and onto, one-to-one correspondence = 전단사 = 일대일 대응

- ref: https://en.wikipedia.org/wiki/Bijection,_injection_and_surjection

Figure: 위키에 있는 단사,전사,전단사함수의 그림

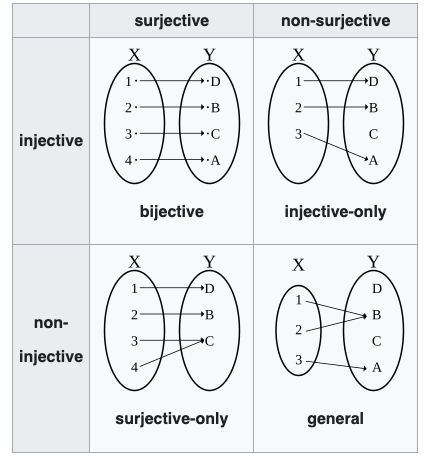
- 따지는 방법

  • 단사: 함수 \(f\)는 \(X\)에서 \(Y\)로 향하는 단사함수이다. \(\Leftrightarrow\) \(\forall x_1,x_2 \in X\): \(x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2)\)
  • 전사: 함수 \(f\)는 \(X\)에서 \(Y\)로 향하는 전사함수이다. \(\Leftrightarrow\) \(\forall y \in Y ~\exists x \in X\) such that \(f(x)=y\).

- 성질1: 어떤함수가 전사함수 & 단사함수 \(\Leftrightarrow\) 전단사함수

- 성질2:

  • 집합 \(X\)에서 집합 \(Y\)로 가는 단사함수 \(f\)가 존재한다. \(\Rightarrow\) \(|X| \leq |Y|\)
  • 집합 \(X\)에서 집합 \(Y\)로 가는 전사함수 \(f\)가 존재한다. \(\Rightarrow\) \(|X| \geq |Y|\)

- 성질1~2로 유추하면 아래와 같은 사실을 주장 할 수 있지 않을까?

  • 집합 \(X\)에서 집합 \(Y\)로 향하는 전단사함수가 존재한다 \(\Rightarrow\) \(|X|=|Y|\)

- 확장된 정의: 두 집합 \(X\), \(Y\)를 고려하자.

  • \(|X|\leq |Y|\) \(\Leftrightarrow\) \(X\)에서 \(Y\)로 향하는 단사함수가 존재한다.
  • \(|X|\geq |Y|\) \(\Leftrightarrow\) \(X\)에서 \(Y\)로 향하는 전사함수가 존재한다.
  • \(|X|=|Y|\) \(\Leftrightarrow\) \(X\)에서 \(Y\)로 향하는 전단사함수가 존재한다.

두 집합의 카디널리티 비교

# 예제1

집합 \(X=\{1,2,3\}\), \(Y=\{2,4,6\}\)을 생각하자. 적당한 함수 \(f\)를 아래와 같이 정의하자.

  • \(f(1)=2\)
  • \(f(2)=4\)
  • \(f(3)=6\)

함수 \(f\)의 성질을 체크해보자.

  1. (단사) \(\forall x_1,x_2 \in X\): \(x_1\neq x_2\) \(\Rightarrow\) \(f(x_1)\neq f(x_2)\).
  2. (전사) \(\forall y \in Y~ \exists x \in X\) such that \(f(x)=y\).

함수 \(f\)는 전단사 함수이다. 집합 \(X\)에서 집합 \(Y\)로 가는 전단사 함수가 존재하므로 집합 \(X\)와 집합 \(Y\)의 카디널리티는 동일하다.

#

# 예제2

집합 \(X=\{1,2,3,\dots \}\), \(Y=\{0,1,2,\dots \}\)을 생각하자. 함수 \(f\)를 아래와 같이 정의하자.

  • \(f(1)=0\)
  • \(f(2)=1\)
  • \(f(3)=2\)
  • \(\dots\)

함수 \(f\)의 성질을 체크해보자.

  1. (단사) \(\forall x_1,x_2 \in X\): \(x_1\neq x_2\) \(\Rightarrow\) \(f(x_1)\neq f(x_2)\)
  2. (전사) \(\forall y \in Y~ \exists x \in X\) such that \(f(x)=y\).

함수 \(f\)는 전단사함수이다. 집합 \(X\)에서 집합 \(Y\)로 가는 전단사 함수가 존재하므로 집합 \(X\)와 집합 \(Y\)의 카디널리티는 동일하다.1

#

- \(\aleph_0\)의 정의: 자연수 집합의 카디널리티 (최소의 무한 기수)를 \(\aleph_0\)이라고 정의한다. 즉

\[|\mathbb{N}|=\aleph_0\]

이다.

- 놀라운 사실1:

  • 음이 아닌 정수의 집합 \(\mathbb{N} \cup \{0\}\)의 카디널리티 역시 \(\aleph_0\)이다.

- 놀라운 사실2:

  • 자연수집합은 음이 아는 정수집합의 진 부분집합인데, 카디널리티가 같다. 즉 \(A \subsetneq B\) 인데, \(|A|=|B|\) 인 상황.
  • 즉 무한집합의 경우, 본인과 카디널넘버가 같은 진 부분집합이 존재할 수 있다. (유한집합에서는 불가능하겠지)
Note

깨알같이 소개하는 무한집합의 정의:

집합 \(A\)가 무한집합이다. \(\Leftrightarrow\) \(A\)와 동일한 카디널리티를 가지는 \(A\)의 진 부분집합이 존재한다.

# 예제3

집합 \(X=\{1,2,3,\dots \}\), \(Y=\{2,4,6,\dots \}\)을 생각하자. 함수 \(f\)를 아래와 같이 정의하자.

  • \(f(1)=2\)
  • \(f(2)=4\)
  • \(f(3)=6\)
  • \(\dots\)

함수 \(f\)의 성질을 체크해보자.

  1. (단사) \(\forall x_1,x_2 \in X\), \(x_1\neq x_2\) \(\Rightarrow\) \(f(x_1)\neq f(x_2)\)?
  2. (전사) \(\forall y \in Y~ \exists x \in X\) such that \(f(x)=y\).

1의 질문과 2의 질문이 모두 맞으므로 함수 \(f\)는 전단사함수이다. 집합 \(X\)에서 집합 \(Y\)로 가는 전단사 함수가 존재하므로 집합 \(X\)와 집합 \(Y\)의 카디널리티는 동일하다.

#

- 인간의 천재적인 직관능력으로 우리는 “\(\aleph_0\)에 1,2,3을 더해도.. 그리고 \(\aleph_0\)를 2배,3배,4배 하여도 \(\aleph_0\)이다” 란 사실을 알 수 있다.

  • \(\aleph_0 + 1 = \aleph_0\)
  • \(\aleph_0 + 2 = \aleph_0\)
  • \(...\)
  • \(\aleph_0 \times 2 = \aleph_0\)
  • \(\aleph_0 \times 3 = \aleph_0\)
  • \(...\)

- 자연수/홀수/짝수/정수의 카디널리티

  • 자연수집합 \(\mathbb{N}\)의 카디널리티는 \(\aleph_0\)이다.
  • 짝수인 자연수 집합의 카디널리티는 \(\aleph_0\)이고, 홀수인 자연수 집합의 카디널리티도 \(\aleph_0\)이다.
  • 정수집합 \(\mathbb{Z}\)의 카디널리티 역시 \(\aleph_0\)이다.

Footnotes

  1. 살짝 어질어질하죠?↩︎