04wk-1: 깊은 신경망 (2) – 꺽인그래프의 한계(?), 시벤코정리, MNIST

Author

최규빈

Published

March 25, 2024

1. 강의영상

2. Imports

import torch
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# import torchvision
# import fastai.data.all

3. 꺽인그래프의 한계?

- 걱정: 지난시간에 배운 기술은 sig를 취하기 전이 꺽은선인 형태만 가능할 듯 하다. 그래서 이 역시 표현력이 부족할 듯 하다.

- 그런데 생각보다 표현력이 풍부한 편이다. 즉 생각보다 쓸 만하다.

A. Step은 표현 불가능하지 않나?

- 맞춰봐

torch.manual_seed(43052)
x = torch.linspace(-1,1,2000).reshape(-1,1)
u = 0*x-3
u[x<-0.2] = (15*x+6)[x<-0.2]
u[(-0.2<x)&(x<0.4)] = (0*x-1)[(-0.2<x)&(x<0.4)]
sig = torch.nn.Sigmoid()
v = π = sig(u)
y = torch.bernoulli(v)
#plt.plot(u,alpha=0.2)
plt.plot(x,y,'.',alpha=0.01,color="C0")
plt.plot(x[0],y[0],'o',color="C0",label=r"observed data (with error): $(x_i,y_i)$")
plt.plot(x,v,'--',label=r"prob (true, unknown): $(x_i,\pi_i)$ or $(x_i,v_i)$",color="C1")
plt.legend()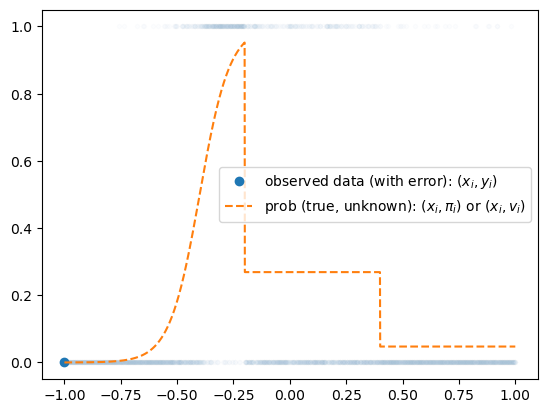

- 저 주황색 구조를 어떻게 표현하지? \(\to\) 선이 많이 꺽이면되는거아냐?

\[\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,256)}{\boldsymbol u^{(1)}} \overset{a_1}{\to} \underset{(n,256)}{\boldsymbol v^{(1)}} \overset{l_1}{\to} \underset{(n,1)}{\boldsymbol u^{(2)}} \overset{a_2}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}}=\underset{(n,1)}{\hat{\boldsymbol y}}\]

#torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(1,256),
    torch.nn.ReLU(),
    torch.nn.Linear(256,1),
    #torch.nn.Sigmoid()
)
#loss_fn = torch.nn.BCELoss()
loss_fn = torch.nn.BCEWithLogitsLoss()
optimizr = torch.optim.Adam(net.parameters())
#--#
for epoc in range(5000):
    ## 1
    yhat = net(x)
    ## 2
    loss = loss_fn(yhat,y)
    ## 3
    loss.backward()
    ## 4
    optimizr.step()
    optimizr.zero_grad()
fig,ax = plt.subplots(1,2)
ax[0].plot(x,u,'--',label=r"$(x_i,u_i)$")
ax[0].plot(x,yhat.data,'--',label=r"$(x_i,\hat{u}_i)$")
ax[0].legend()
ax[0].set_title("before sig")
ax[1].plot(x,y,'.',alpha=0.02,color="blue")
ax[1].plot(x,v,'--', color="C0", label=r"$(x_i,v_i)$ or $(x_i,\pi_i)$")
ax[1].plot(x,sig(yhat.data),'--',color="C1",label=r"$(x_i,\hat{v}_i)$ or $(x_i,\hat{\pi}_i)$")
ax[1].legend()
ax[1].set_title("after sig")
Text(0.5, 1.0, 'after sig')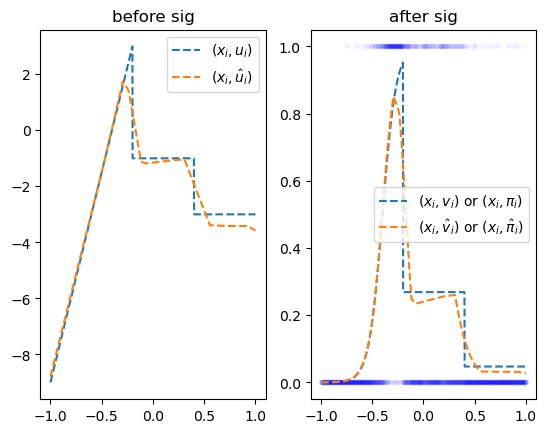

B. 곡선은 표현 불가능하지 않나?

- 맞춰봐1

  • 1 2024년 수능 미적30번 문제에 나온 함수응용

    • \[y_i = e^{-x_i} \times |\cos(5x_i)| \times \sin(5x) + \epsilon_i, \quad \epsilon_i \sim N(0,\sigma^2)\]

    torch.manual_seed(43052)
x = torch.linspace(0,2,2000).reshape(-1,1)
eps = torch.randn(2000).reshape(-1,1)*0.05
fx = torch.exp(-1*x)* torch.abs(torch.cos(3*x))*(torch.sin(3*x))
y = fx + eps
    plt.plot(x,y,label=r"observed data (with error): $(x_i,y_i)$", alpha=0.2)
plt.plot(x,fx,'--',color="C0",label=r"underlying (true, unknown): $e^{-x}|\cos(3x)|\sin(3x)$")
plt.legend()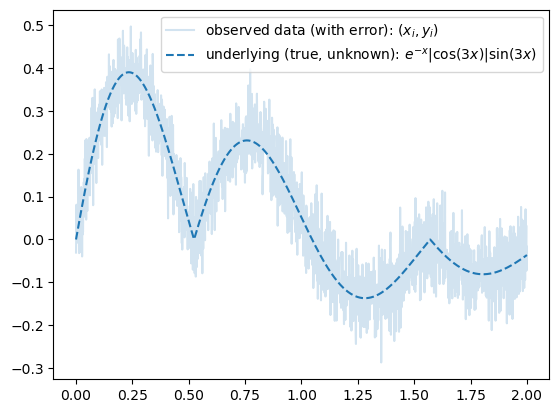

    - 맞춰본다..

    • \(\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,1024)}{\boldsymbol u^{(1)}} \overset{a_1}{\to} \underset{(n,1024)}{\boldsymbol v^{(1)}} \overset{l_1}{\to} \underset{(n,1)}{\boldsymbol u^{(2)}} \overset{a_2}{\to} \underset{(n,1)}{\boldsymbol v^{(2)}}=\underset{(n,1)}{\hat{\boldsymbol y}}\)
    #torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(1,1024),
    torch.nn.ReLU(),
    torch.nn.Linear(1024,1)
)
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters())
#--#
for epoc in range(5000):
    ## 1
    yhat = net(x)
    ## 2
    loss = loss_fn(yhat,y)
    ## 3
    loss.backward()
    ## 4
    optimizr.step()
    optimizr.zero_grad()
    plt.plot(x,y,label=r"observed data: $(x_i,y_i)$", alpha=0.2)
plt.plot(x,fx,'--',color="C0",label=r"underlying (true, unkown): $e^{-x}|\cos(3x)|\sin(3x)$")
plt.plot(x,yhat.data,'--',color="C1",label=r"underlying (esimated): $(x_i,\hat{y}_i)$")
plt.legend()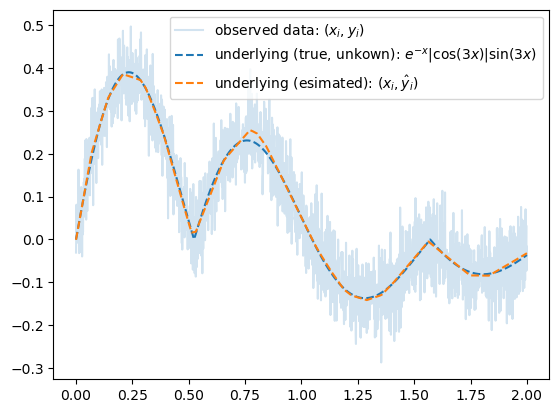

    4. 시벤코정리

    A. 시벤코의 정리 소개

    Universal Approximation Thm (Cybenko 1989)

    하나의 은닉층을 가지는 아래와 같은 꼴의 네트워크 \(net: {\bf X}_{n \times p} \to {\bf y}_{n\times q}\)는

    net = torch.nn.Sequential(
    torch.nn.Linear(p,???),
    torch.nn.Sigmoid(),
    torch.nn.Linear(???,q)
)

    모든 continuous mapping

    \[f: {\bf X}_{n \times p} \to {\bf y}_{n\times q}\]

    를 원하는 정확도로 “근사”시킬 수 있다. 쉽게 말하면 \({\bf X} \to {\bf y}\) 인 어떠한 복잡한 규칙라도 하나의 은닉층을 가진 신경망이 원하는 정확도로 근사시킨다는 의미이다. 예를들면 아래와 같은 문제를 해결할 수 있다.

    • \({\bf X}\)는 토익점수, GPA, 공모전참가여부, \({\bf y}\)는 취업여부일 경우 \({\bf X} \to {\bf y}\)인 규칙을 심층신경망은 항상 찾을 수 있다.
    • \({\bf X}\)는 주택이미지, 지역정보, 주택면적, 주택에 대한 설명 \({\bf y}\)는 주택가격일 경우 \({\bf X} \to {\bf y}\)인 규칙을 심층신경망은 항상 찾을 수 있다.

    즉 하나의 은닉층을 가진 신경망의 표현력은 무한대라 볼 수 있다.

    Cybenko, George. 1989. “Approximation by Superpositions of a Sigmoidal Function.” Mathematics of Control, Signals and Systems 2 (4): 303–14.

    B. 왜 가능한가?

    - 데이터

    x = torch.linspace(-10,10,200).reshape(-1,1)

    - 아래와 같은 네트워크를 고려하자. (스펙올라도 취업못하는 예제에서 썼던 네크워크랑 비슷해요)

    l1 = torch.nn.Linear(in_features=1,out_features=2)
a1 = torch.nn.Sigmoid()
l2 = torch.nn.Linear(in_features=2,out_features=1)

    - 직관1: \(l_1\),\(l_2\)의 가중치를 잘 결합하다보면 우연히 아래와 같이 만들 수 있다.

    l1.weight.data = torch.tensor([[-5.00],[5.00]])
l1.bias.data = torch.tensor([+10.00,+10.00])
    l2.weight.data = torch.tensor([[1.00,1.00]])
l2.bias.data = torch.tensor([-1.00])
    fig,ax = plt.subplots(1,3,figsize=(9,3))
ax[0].plot(x,l1(x)[:,[0]].data,label=r"$-5x+10$")
ax[0].plot(x,l1(x)[:,[1]].data,label=r"$5x+10$")
ax[0].set_title('$l_1(x)$')
ax[0].legend()
ax[1].plot(x,a1(l1(x))[:,[0]].data,label=r"$v_1=sig(-5x+10)$")
ax[1].plot(x,a1(l1(x))[:,[1]].data,label=r"$v_2=sig(5x+10)$")
ax[1].set_title('$(a_1 \circ l_1)(x)$')
ax[1].legend()
ax[2].plot(x,l2(a1(l1(x))).data,color='C2',label=r"$v_1+v_2-1$")
ax[2].set_title('$(l_2 \circ a_1 \circ \l_1)(x)$')
ax[2].legend()
    <>:8: SyntaxWarning: invalid escape sequence '\c'
<>:11: SyntaxWarning: invalid escape sequence '\c'
<>:8: SyntaxWarning: invalid escape sequence '\c'
<>:11: SyntaxWarning: invalid escape sequence '\c'
/tmp/ipykernel_31460/3092854458.py:8: SyntaxWarning: invalid escape sequence '\c'
  ax[1].set_title('$(a_1 \circ l_1)(x)$')
/tmp/ipykernel_31460/3092854458.py:11: SyntaxWarning: invalid escape sequence '\c'
  ax[2].set_title('$(l_2 \circ a_1 \circ \l_1)(x)$')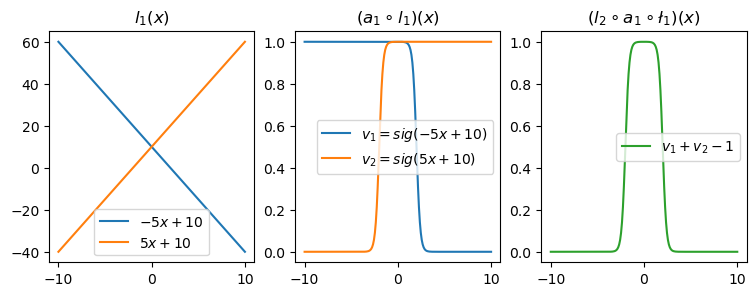

    - 직관2: 아래들도 가능할듯?

    l1.weight.data = torch.tensor([[-5.00],[5.00]])
l1.bias.data = torch.tensor([+0.00,+20.00])
l2.weight.data = torch.tensor([[1.00,1.00]])
l2.bias.data = torch.tensor([-1.00])
fig,ax = plt.subplots(1,3,figsize=(9,3))
ax[0].plot(x,l1(x).data.numpy(),'--',color='C0'); ax[0].set_title('$l_1(x)$')
ax[1].plot(x,a1(l1(x)).data.numpy(),'--',color='C0'); ax[1].set_title('$(a_1 \circ l_1)(x)$')
ax[2].plot(x,l2(a1(l1(x))).data,'--',color='C0'); ax[2].set_title('$(l_2 \circ a_1 \circ \l_1)(x)$');
ax[2].set_ylim(-0.1,2.6)
    <>:7: SyntaxWarning: invalid escape sequence '\c'
<>:8: SyntaxWarning: invalid escape sequence '\c'
<>:7: SyntaxWarning: invalid escape sequence '\c'
<>:8: SyntaxWarning: invalid escape sequence '\c'
/tmp/ipykernel_31460/3368460049.py:7: SyntaxWarning: invalid escape sequence '\c'
  ax[1].plot(x,a1(l1(x)).data.numpy(),'--',color='C0'); ax[1].set_title('$(a_1 \circ l_1)(x)$')
/tmp/ipykernel_31460/3368460049.py:8: SyntaxWarning: invalid escape sequence '\c'
  ax[2].plot(x,l2(a1(l1(x))).data,'--',color='C0'); ax[2].set_title('$(l_2 \circ a_1 \circ \l_1)(x)$');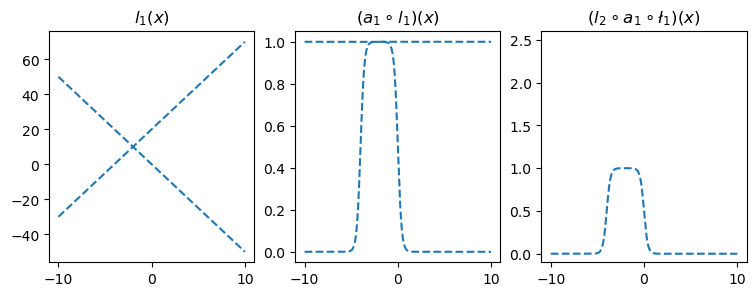

    l1.weight.data = torch.tensor([[-5.00],[5.00]])
l1.bias.data = torch.tensor([+20.00,+00.00])
l2.weight.data = torch.tensor([[2.50,2.50]])
l2.bias.data = torch.tensor([-2.50])
fig,ax = plt.subplots(1,3,figsize=(9,3))
ax[0].plot(x,l1(x).data.numpy(),'--',color='C1'); ax[0].set_title('$l_1(x)$')
ax[1].plot(x,a1(l1(x)).data.numpy(),'--',color='C1'); ax[1].set_title('$(a_1 \circ l_1)(x)$')
ax[2].plot(x,l2(a1(l1(x))).data,'--',color='C1'); ax[2].set_title('$(l_2 \circ a_1 \circ \l_1)(x)$');
ax[2].set_ylim(-0.1,2.6)
    <>:7: SyntaxWarning: invalid escape sequence '\c'
<>:8: SyntaxWarning: invalid escape sequence '\c'
<>:7: SyntaxWarning: invalid escape sequence '\c'
<>:8: SyntaxWarning: invalid escape sequence '\c'
/tmp/ipykernel_31460/2330299143.py:7: SyntaxWarning: invalid escape sequence '\c'
  ax[1].plot(x,a1(l1(x)).data.numpy(),'--',color='C1'); ax[1].set_title('$(a_1 \circ l_1)(x)$')
/tmp/ipykernel_31460/2330299143.py:8: SyntaxWarning: invalid escape sequence '\c'
  ax[2].plot(x,l2(a1(l1(x))).data,'--',color='C1'); ax[2].set_title('$(l_2 \circ a_1 \circ \l_1)(x)$');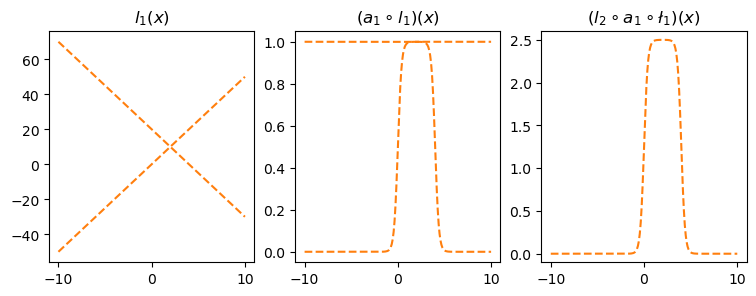

    - 직관3: 은닉층의노드수=4로 하고 적당한 가중치를 조정하면 \((l_2\circ a_1 \circ l_1)(x)\)의 결과로 주황색선 + 파란색선도 가능할 것 같다. \(\to\) 실제로 가능함

    l1 = torch.nn.Linear(in_features=1,out_features=4)
a1 = torch.nn.Sigmoid()
l2 = torch.nn.Linear(in_features=4,out_features=1)
    l1.weight.data = torch.tensor([[-5.00],[5.00],[-5.00],[5.00]])
l1.bias.data = torch.tensor([0.00, 20.00, 20.00, 0])
l2.weight.data = torch.tensor([[1.00,  1.00, 2.50,  2.50]])
l2.bias.data = torch.tensor([-1.0-2.5])
    plt.plot(l2(a1(l1(x))).data,'--')
plt.title(r"$(l_2 \circ a_1 \circ l_1)(x)$")
    Text(0.5, 1.0, '$(l_2 \\circ a_1 \\circ l_1)(x)$')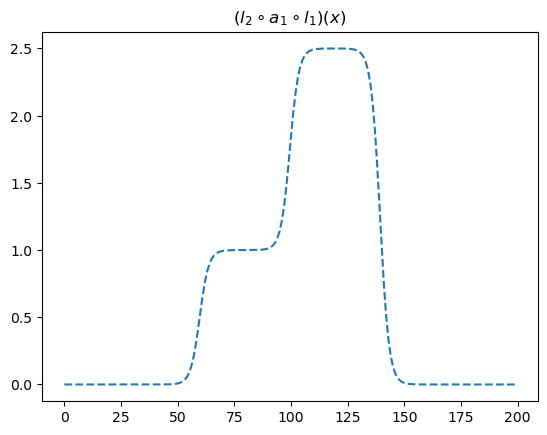

    이러한 함수는 계단모양이며, 0을 제외한 서로다른 계단의 높이는 2개가 된다. 이를 간단히 “2단계-계단함수”라고 칭하자.

    - 정리1: 2개의 시그모이드를 우연히 잘 결합하면 아래와 같은 “1단계-계단함수” 함수 \(h\)를 만들 수 있다.

    h = lambda x: torch.sigmoid(200*(x+0.5))+torch.sigmoid(-200*(x-0.5))-1.0
    plt.plot(x,h(x))
plt.title("$h(x)$")
    Text(0.5, 1.0, '$h(x)$')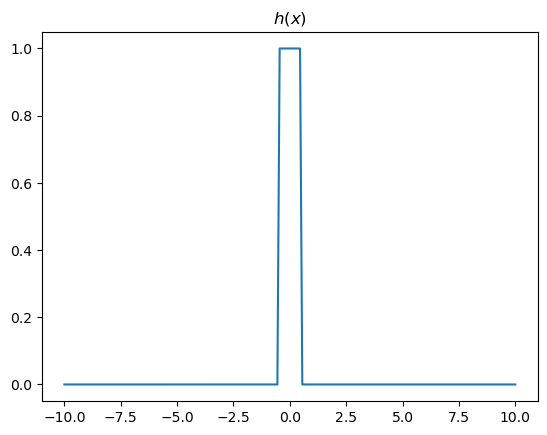

    - 정리2: 위와 같은 함수 \(h\)를 활성화함수로 하고 \(m\)개의 노드를 가지는 은닉층을 생각해보자. 이러한 은닉층을 사용한다면 “m단계-계단함수”와 같은 형태의 네트워크는 아래와 같이 \(m\)개의 은닉노드를 써서 항상 표현할 수 있다.

    \[\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,m)}{\boldsymbol u^{(1)}} \overset{h}{\to} \underset{(n,m)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\hat{\boldsymbol y}}\]

    그리고 위의 네트워크와 동일한 효과를 주는 아래의 네트워크가 항상 존재함.

    \[\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,2m)}{\boldsymbol u^{(1)}} \overset{sig}{\to} \underset{(n,2m)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\hat{\boldsymbol y}}\]

    - 직관4: 그런데 어떠한 함수형태라도 구불구불한 “m단계-계단함수”로 다 근사할 수 있지 않나?

    C. \(h\)의 위력

    - \(h(x)\)를 생성하는 클래스를 만들어보자.

    class MyActivation(torch.nn.Module): ## 사용자정의 활성화함수를 선언하는 방법
    def __init__(self):
        super().__init__()
    def forward(self, u):
        h = lambda x: torch.sigmoid(200*(x+0.5))+torch.sigmoid(-200*(x-0.5))-1.0
        v = h(u)
        return v # activation 의 출력
    a1 = MyActivation()
# a1 = torch.nn.Sigmoid(), a1 = torch.nn.ReLU() 대신에 a1 = MyActivation()

    - 아래와 같이 하나의 은닉층을 가지고 있더라도 많은 노드수만 보장되면 매우 충분한 표현력을 가짐

    \[\underset{(n,1)}{\bf X} \overset{l_1}{\to} \underset{(n,m)}{\boldsymbol u^{(1)}} \overset{h}{\to} \underset{(n,m)}{\boldsymbol v^{(1)}} \overset{l_2}{\to} \underset{(n,1)}{\hat{\boldsymbol y}}\]

    - \(h\)의 위력

    예제1 – 스펙높아도 취업이 안된다고??

    df = pd.read_csv("https://raw.githubusercontent.com/guebin/DL2024/main/posts/dnnex.csv")
x = torch.tensor(df.x).float().reshape(-1,1)
y = torch.tensor(df.y).float().reshape(-1,1)
prob = torch.tensor(df.prob).float().reshape(-1,1)
    torch.manual_seed(43052)
class MyActivation(torch.nn.Module):
    def __init__(self):
        super().__init__()
    def forward(self, u):
        h = lambda x: torch.sigmoid(200*(x+0.5))+torch.sigmoid(-200*(x-0.5))-1.0
        v = h(u)
        return v
#---#
net = torch.nn.Sequential(
    torch.nn.Linear(1,2048),
    MyActivation(),
    torch.nn.Linear(2048,1),
    torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters())
#---#
for epoc in range(100):
    ## 1
    yhat = net(x)
    ## 2
    loss = loss_fn(yhat,y)
    ## 3
    loss.backward()
    ## 4
    optimizr.step()
    optimizr.zero_grad()
    plt.plot(x,y,'o',alpha=0.2, label="observed data (with error)")
plt.plot(x,prob,'--', label="prob (true, unknown)")
plt.plot(x,net(x).data,'--',label="prob (estimated)")
plt.legend()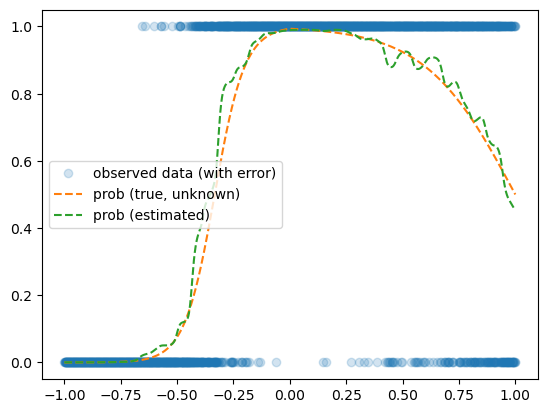

    예제2 – 수능에 나왔다던 이상한 곡선..?

    torch.manual_seed(43052)
x = torch.linspace(0,2,2000).reshape(-1,1)
eps = torch.randn(2000).reshape(-1,1)*0.05
fx = torch.exp(-1*x)* torch.abs(torch.cos(3*x))*(torch.sin(3*x))
y = fx + eps
    torch.manual_seed(43052)
class MyActivation(torch.nn.Module):
    def __init__(self):
        super().__init__()
    def forward(self, u):
        h = lambda x: torch.sigmoid(200*(x+0.5))+torch.sigmoid(-200*(x-0.5))-1.0
        v = h(u)
        return v
#---#
net = torch.nn.Sequential(
    torch.nn.Linear(1,2048),
    MyActivation(),
    torch.nn.Linear(2048,1),
)
loss_fn = torch.nn.MSELoss()
optimizr = torch.optim.Adam(net.parameters())
#---#
for epoc in range(100):
    ## 1
    yhat = net(x)
    ## 2
    loss = loss_fn(yhat,y)
    ## 3
    loss.backward()
    ## 4
    optimizr.step()
    optimizr.zero_grad()
    plt.plot(x,y,alpha=0.2,label="observed data (with error)")
plt.plot(x,fx,'--',label="underlying (true, unknown)")
plt.plot(x,net(x).data,'--',label="underlying (estimated)")
plt.legend()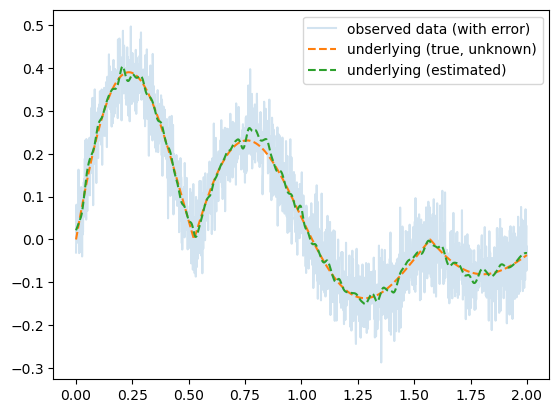

    D. 의문점

    - 이 수업을 잘 이해한 사람: 그냥 활성화함수를 \(h\)로 쓰면 끝 아니야? 뭐하러 relu 를 쓰는거지?

    - 딥러닝을 좀 공부해본사람1: 왜 딥러닝이 2010년이 지나서야 떳지? 1989년에 세상의 모든 문제가 풀려야 하는것 아닌가?

    - 딥러닝을 좀 공부해본사람2: 하나의 은닉층을 표현하는 네크워크는 잘 안쓰지 않나? 은닉층이 많을수록 좋다고 들었는데?

    - 약간의 의구심이 있지만 아무튼 우리는 아래의 무기를 가진 꼴이 되었다.

    우리의 무기

    하나의 은닉층을 가지는 아래와 같은 꼴의 네트워크로,

    net = torch.nn.Sequential(
    torch.nn.Linear(p,???),
    torch.nn.Sigmoid(),
    torch.nn.Linear(???,q)
)

    \(f: {\bf X}_{n \times p} \to {\bf y}_{n\times q}\) 인 모든 continuous mapping \(f\) 을 원하는 정확도로 “근사”시킬 수 있다.

    5. MNIST 해결

    A. 데이터 다운로드

    import fastai.data.all
    fastai.data.external.untar_data('https://s3.amazonaws.com/fast-ai-imageclas/mnist_png.tgz')
    100.03% [15687680/15683414 00:03<00:00] 
    Path('/root/.fastai/data/mnist_png')
    !ls '/root/.fastai/data/mnist_png'
    testing  training
    !ls '/root/.fastai/data/mnist_png/training/'
    0  1  2  3  4  5  6  7  8  9
    !ls '/root/.fastai/data/mnist_png/training/3' | head
    10.png
10000.png
10011.png
10031.png
10034.png
10042.png
10052.png
1007.png
10074.png
10091.png
ls: write error: Broken pipe
    import torchvision
    img3 = torchvision.io.read_image('/root/.fastai/data/mnist_png/training/3/10.png')
plt.imshow(img3.reshape(28,28),cmap="gray")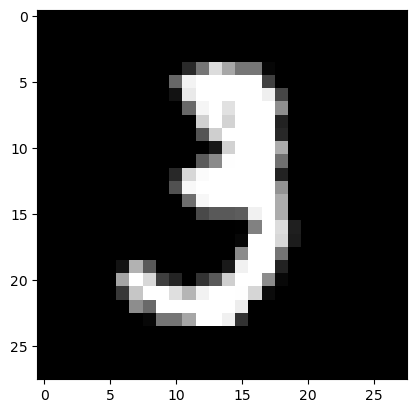

    B. 예비학습 – `plt.imshow()

    - plt.imshow(...) 에서 ...이 shape이 (??,??)이면 흑백이미지를 출력

    plt.imshow([[0,255],[0,255]],cmap='gray')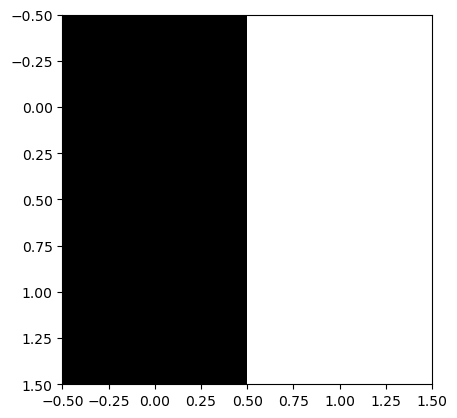

    - plt.imshow(...) 에서 ...의 shape이 (??,??,3)이면 칼라이미지를 출력

    r = [[0,255],[0,255]]
g = [[255,0],[0,0]]
b = [[0,0],[255,0]]
plt.imshow(np.stack([r,g,b],axis=2))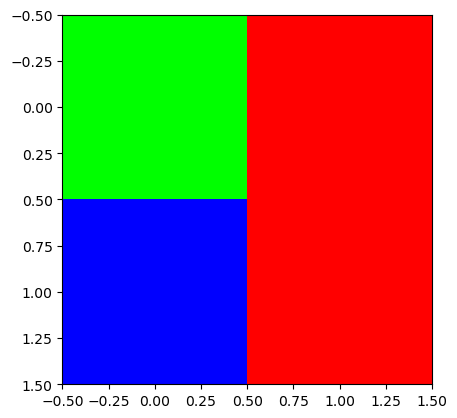

    - plt.imshow(...) 에서 ...의 자료형이 int인지 float인지에 따라서 인식이 다름

    r = [[0,1],[0,1]]
g = [[1,0],[0,0]]
b = [[0,0],[1,0]]
plt.imshow(np.stack([r,g,b],axis=2))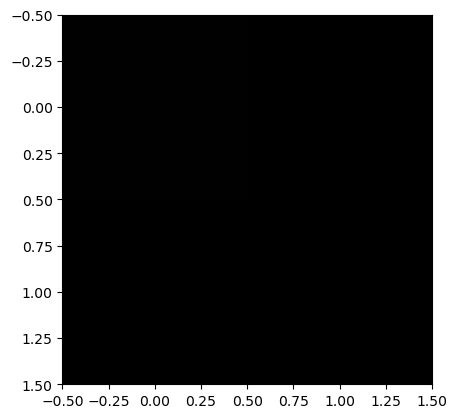

    r = [[0,1.0],[0,1.0]]
g = [[1.0,0],[0,0]]
b = [[0,0],[1.0,0]]
plt.imshow(np.stack([r,g,b],axis=2))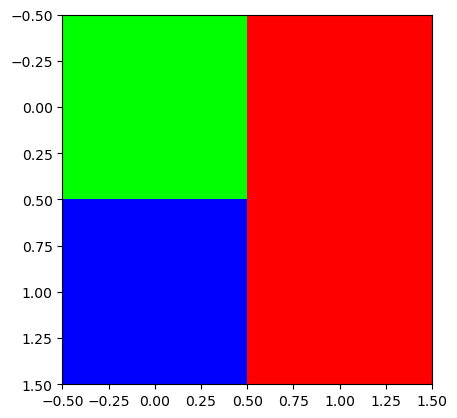

    C. 예비학습 – pathlib

    - 오브젝트 생성

    path = fastai.imports.Path('.')
path
    Path('.')

    - 기능1 – .ls()

    path.ls()
    (#6) [Path('.ipynb_checkpoints'),Path('05wk-2.ipynb'),Path('06wk-1.ipynb'),Path('01wk-1.ipynb'),Path('05wk-1.ipynb'),Path('04wk-1.ipynb')]

    - 이미지 파일이 저장된 경로로 새로운 path오브젝트를 만들고 기능1 수행

    path = fastai.imports.Path('/root/.fastai/data/mnist_png')
path
    Path('/root/.fastai/data/mnist_png')
    path.ls()
    (#2) [Path('/root/.fastai/data/mnist_png/training'),Path('/root/.fastai/data/mnist_png/testing')]

    - 기능2: / 로 새로운 path 생성하기

    (path / 'training')
    Path('/root/.fastai/data/mnist_png/training')

    - 기능1,2의 결합

    (path / 'training').ls()
    (#10) [Path('/root/.fastai/data/mnist_png/training/5'),Path('/root/.fastai/data/mnist_png/training/3'),Path('/root/.fastai/data/mnist_png/training/7'),Path('/root/.fastai/data/mnist_png/training/8'),Path('/root/.fastai/data/mnist_png/training/1'),Path('/root/.fastai/data/mnist_png/training/4'),Path('/root/.fastai/data/mnist_png/training/6'),Path('/root/.fastai/data/mnist_png/training/2'),Path('/root/.fastai/data/mnist_png/training/0'),Path('/root/.fastai/data/mnist_png/training/9')]

    D. 데이터정리

    - 데이터가 저장된 path 설정

    path = fastai.imports.Path('/root/.fastai/data/mnist_png')

    - X ,y를 만듦

    X3 = torch.stack([torchvision.io.read_image(str(i)) for i in (path/'training/3').ls()],axis=0)
X7 = torch.stack([torchvision.io.read_image(str(i)) for i in (path/'training/7').ls()],axis=0)
    X3.shape, X7.shape
    (torch.Size([6131, 1, 28, 28]), torch.Size([6265, 1, 28, 28]))
    y = torch.tensor([0.0]*6131+[1.0]*6265).reshape(-1,1)
    X = torch.concat([X3,X7],axis=0)
X.shape
    torch.Size([12396, 1, 28, 28])
    plt.plot(y,'o')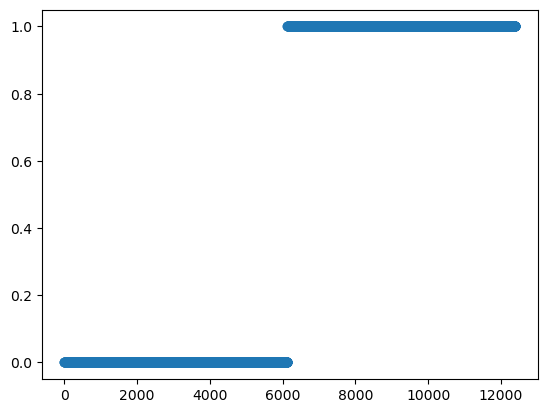

    • “y=0.0” 은 숫자3을 의미함, “y=1.0” 은 숫자7을 의미함
    • 숫자3은 6131개, 숫자7은 6265개 있음

    - 우리는 \({\bf X}: (n,1,28,28)\) 에서 \({\bf y}: (n,1)\)으로 가는 맵핑을 배우고 싶음. \(\to\) 이런건 배운적이 없는데?.. \(\to\) 그렇다면 \({\bf X}:(n,784) \to {\bf y}:(n,1)\) 으로 가는 맵핑을 학습하자.

    X = torch.concat([X3,X7],axis=0).reshape(-1,28*28).float()
X.shape, y.shape
    (torch.Size([12396, 784]), torch.Size([12396, 1]))

    E. 학습

    torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(784,32),
    torch.nn.ReLU(),
    torch.nn.Linear(32,1),
    torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters())
#--#
for epoc in range(200):
    ## step1
    yhat = net(X)
    ## step2
    loss = loss_fn(yhat,y)
    ## step3
    loss.backward()
    ## step4
    optimizr.step()
    optimizr.zero_grad()
    plt.plot(y,'o',label=r"$(i,y_i)$ -- training data set")
plt.plot(net(X).data,'.',alpha=0.2, label=r"$(i,\hat{y}_i$ -- training data set")
plt.legend()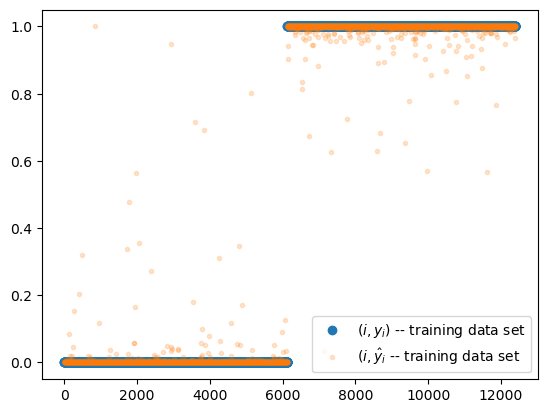

    • 잘맞추는데?
    • 믿을수가 없는데..?
    ((yhat.data > 0.5) == y).float().mean() # train_accuracy
    tensor(0.9994)

    F. Test

    path.ls()
    (#2) [Path('/root/.fastai/data/mnist_png/training'),Path('/root/.fastai/data/mnist_png/testing')]
    XX3 = torch.stack([torchvision.io.read_image(str(i)) for i in (path/'testing/3').ls()],axis=0)
XX7 = torch.stack([torchvision.io.read_image(str(i)) for i in (path/'testing/7').ls()],axis=0)
    XX3.shape,XX7.shape
    (torch.Size([1010, 1, 28, 28]), torch.Size([1028, 1, 28, 28]))
    XX = torch.concatenate([XX3,XX7],axis=0).reshape(-1,1*28*28).float()
XX.shape
    torch.Size([2038, 784])
    yy = torch.tensor([0]*1010 + [1]*1028).reshape(-1,1).float()
yy.shape
    torch.Size([2038, 1])
    plt.plot(yy,'o',label=r"$(i,y_i)$ -- test data set")
plt.plot(net(XX).data,'.',label=r"$(i,\hat{y}_i)$ -- test data set")
plt.legend()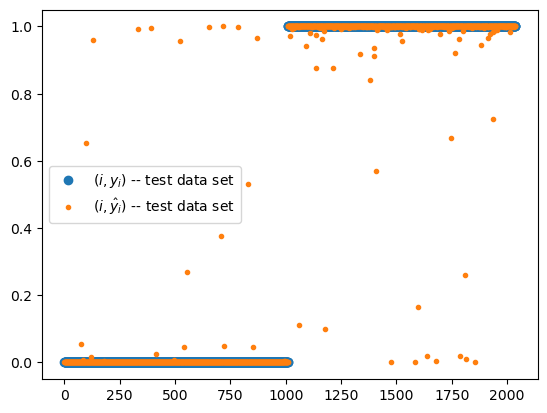

    (yy == (net(XX)>0.5)).float().mean() # test accuracy
    tensor(0.9897)
    • test 에서도 잘 맞춘다..

    6. HW

    # 5. MNIST 해결 -- E. 학습 에 소개된 학습코드는 아래와 같다.

    torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(784,32),
    torch.nn.ReLU(),
    torch.nn.Linear(32,1),
    torch.nn.Sigmoid()
)
loss_fn = torch.nn.BCELoss()
optimizr = torch.optim.Adam(net.parameters())
#--#
for epoc in range(200):
    ## step1
    yhat = net(X)
    ## step2
    loss = loss_fn(yhat,y)
    ## step3
    loss.backward()
    ## step4
    optimizr.step()
    optimizr.zero_grad()

    이 코드에 사용된 네트워크를 아래와 같이 변형하고, 적절한 loss_fn 을 다시 정의하여 학습하라.

    torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(784,32),
    torch.nn.ReLU(),
    torch.nn.Linear(32,1)
    #torch.nn.Sigmoid()
)

    학습결과를 확인하고 accuracy를 구하라.

    (풀이)

    ## Step1 
path = fastai.imports.Path('/root/.fastai/data/mnist_png')
X3 = torch.stack([torchvision.io.read_image(str(i)) for i in (path/'training/3').ls()],axis=0)
X7 = torch.stack([torchvision.io.read_image(str(i)) for i in (path/'training/7').ls()],axis=0)
X = torch.concat([X3,X7],axis=0).reshape(-1,28*28).float()
y = torch.tensor([0.0]*6131+[1.0]*6265).reshape(-1,1)
## Step2 
torch.manual_seed(43052)
net = torch.nn.Sequential(
    torch.nn.Linear(784,32),
    torch.nn.ReLU(),
    torch.nn.Linear(32,1),
)
loss_fn = torch.nn.BCEWithLogitsLoss()
optimizr = torch.optim.Adam(net.parameters())
## Step3 
for epoc in range(200):
    ## step1
    netout = net(X)
    ## step2
    loss = loss_fn(netout,y)
    ## step3
    loss.backward()
    ## step4
    optimizr.step()
    optimizr.zero_grad()
## Step4 
sig = torch.nn.Sigmoid()
print(f'acc(방법1) = {((sig(netout) > 0.5) == y).float().mean()}')
print(f'acc(방법2) = {((netout>0) == y).float().mean()}')
    acc(방법1) = 0.999515950679779
acc(방법2) = 0.999515950679779
    • 두번째 방법은 시그모이드 취하기전의 값이 0보다 커야, 시그모이드를 취한 값이 0.5 이상이 됨을 이용한 것이다. (참고로 시그모이드 취하기 전의 값이 딱 0이라면 시그모이드를 취한값은 0.5가 된다) 즉 \(netout>0 \Leftrightarrow sig(netout)>0.5\)를 이용한 것임.