import torch
import matplotlib.pyplot as plt
import numpy as np02wk-2: 회귀분석 (3) – Step1,2,4 의 변형
1. 강의영상
2. Imports
3. 회귀분석 예제의 다양한 구현
A. Data
temp = [-2.4821, -2.3621, -1.9973, -1.6239, -1.4792, -1.4635, -1.4509, -1.4435,
-1.3722, -1.3079, -1.1904, -1.1092, -1.1054, -1.0875, -0.9469, -0.9319,
-0.8643, -0.7858, -0.7549, -0.7421, -0.6948, -0.6103, -0.5830, -0.5621,
-0.5506, -0.5058, -0.4806, -0.4738, -0.4710, -0.4676, -0.3874, -0.3719,
-0.3688, -0.3159, -0.2775, -0.2772, -0.2734, -0.2721, -0.2668, -0.2155,
-0.2000, -0.1816, -0.1708, -0.1565, -0.1448, -0.1361, -0.1057, -0.0603,
-0.0559, -0.0214, 0.0655, 0.0684, 0.1195, 0.1420, 0.1521, 0.1568,
0.2646, 0.2656, 0.3157, 0.3220, 0.3461, 0.3984, 0.4190, 0.5443,
0.5579, 0.5913, 0.6148, 0.6469, 0.6469, 0.6523, 0.6674, 0.7059,
0.7141, 0.7822, 0.8154, 0.8668, 0.9291, 0.9804, 0.9853, 0.9941,
1.0376, 1.0393, 1.0697, 1.1024, 1.1126, 1.1532, 1.2289, 1.3403,
1.3494, 1.4279, 1.4994, 1.5031, 1.5437, 1.6789, 2.0832, 2.2444,
2.3935, 2.6056, 2.6057, 2.6632]
sales= [-8.5420, -6.5767, -5.9496, -4.4794, -4.2516, -3.1326, -4.0239, -4.1862,
-3.3403, -2.2027, -2.0262, -2.5619, -1.3353, -2.0466, -0.4664, -1.3513,
-1.6472, -0.1089, -0.3071, -0.6299, -0.0438, 0.4163, 0.4166, -0.0943,
0.2662, 0.4591, 0.8905, 0.8998, 0.6314, 1.3845, 0.8085, 1.2594,
1.1211, 1.9232, 1.0619, 1.3552, 2.1161, 1.1437, 1.6245, 1.7639,
1.6022, 1.7465, 0.9830, 1.7824, 2.1116, 2.8621, 2.1165, 1.5226,
2.5572, 2.8361, 3.3956, 2.0679, 2.8140, 3.4852, 3.6059, 2.5966,
2.8854, 3.9173, 3.6527, 4.1029, 4.3125, 3.4026, 3.2180, 4.5686,
4.3772, 4.3075, 4.4895, 4.4827, 5.3170, 5.4987, 5.4632, 6.0328,
5.2842, 5.0539, 5.4538, 6.0337, 5.7250, 5.7587, 6.2020, 6.5992,
6.4621, 6.5140, 6.6846, 7.3497, 8.0909, 7.0794, 6.8667, 7.4229,
7.2544, 7.1967, 9.5006, 9.0339, 7.4887, 9.0759, 11.0946, 10.3260,
12.2665, 13.0983, 12.5468, 13.8340]
x = torch.tensor(temp).reshape(-1,1)
ones = torch.ones(100).reshape(-1,1)
X = torch.concat([ones,x],axis=1)
y = torch.tensor(sales).reshape(-1,1)B. 파이토치를 이용한 학습
- 외우세여
What = torch.tensor([[-5.0],[10.0]],requires_grad = True)
for epoc in range(30):
# step1: yhat
yhat = X@What
# step2: loss
loss = torch.sum((y-yhat)**2)
# step3: 미분
loss.backward()
# step4: update
What.data = What.data - 0.001 * What.grad
What.grad = None- 결과 시각화
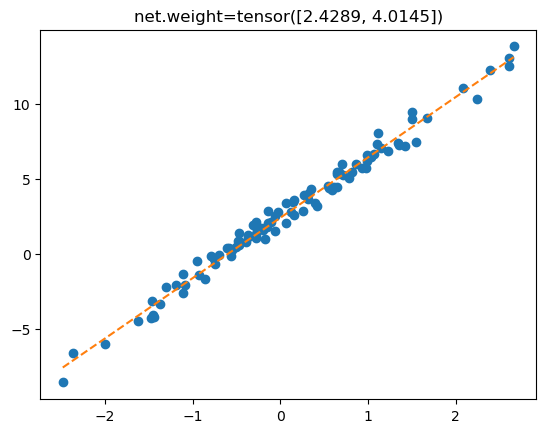
plt.plot(x,y,'o')
plt.plot(x,X@What.data,'--')
plt.title(f'What={What.data.reshape(-1)}');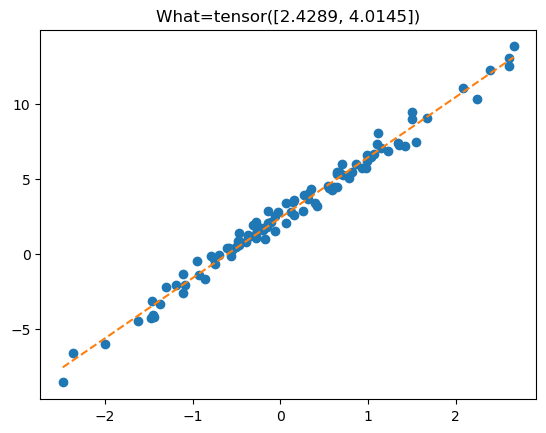
C. Step2의 수정
- 수정된 코드
What = torch.tensor([[-5.0],[10.0]],requires_grad = True)
loss_fn = torch.nn.MSELoss()
for epoc in range(30):
# step1: yhat
yhat = X@What
# step2: loss
#loss = torch.sum((y-yhat)**2)/100
#loss = torch.mean((y-yhat)**2)
loss = loss_fn(yhat,y) # 여기서는 큰 상관없지만 습관적으로 yhat을 먼저넣는 연습을 하자!!
# step3: 미분
loss.backward()
# step4: update
What.data = What.data - 0.1 * What.grad
What.grad = None- 결과확인
plt.plot(x,y,'o')
plt.plot(x,X@What.data,'--')
plt.title(f'What={What.data.reshape(-1)}');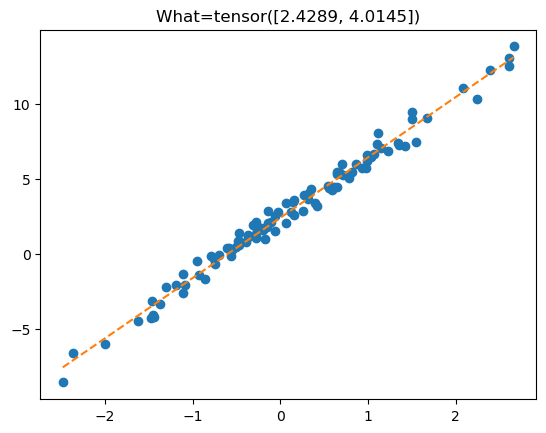
D. Step1의 수정 – net의 이용
- net 오브젝트란?
원래 yhat을 이런식으로 구했는데 ~
What = torch.tensor([[-5.0],[10.0]],requires_grad = True)
(X@What.data)[:5]tensor([[-29.8210],
[-28.6210],
[-24.9730],
[-21.2390],
[-19.7920]])이런식으로도 구할수 있음!
net = torch.nn.Linear(
in_features=2,
out_features=1,
bias=False
)net.weight.data = torch.tensor([[-5.0, 10.0]])
net.weightParameter containing:
tensor([[-5., 10.]], requires_grad=True)net(X)[:5]tensor([[-29.8210],
[-28.6210],
[-24.9730],
[-21.2390],
[-19.7920]], grad_fn=<SliceBackward0>)- 학습
# step1을 위한 사전준비
net = torch.nn.Linear(
in_features=2,
out_features=1,
bias=False
)
net.weight.data = torch.tensor([[-5.0, 10.0]])
# step2를 위한 사전준비
loss_fn = torch.nn.MSELoss()
for epoc in range(30):
# step1: yhat
yhat = net(X)
# step2: loss
loss = loss_fn(yhat,y)
# step3: 미분
loss.backward()
# step4: update
net.weight.data = net.weight.data - 0.1 * net.weight.grad
net.weight.grad = None- 결과확인
plt.plot(x,y,'o')
plt.plot(x,net(X).data,'--')
plt.title(f'net.weight={net.weight.data.reshape(-1)}');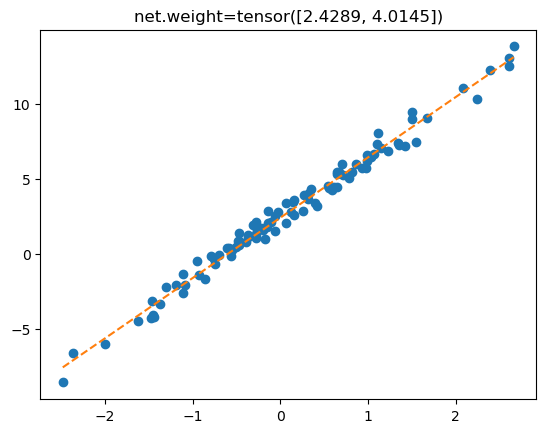
E. Step4의 수정 – optimizer의 이용
기존코드의 에폭별분해
- 준비과정
# step1을 위한 사전준비
net = torch.nn.Linear(
in_features=2,
out_features=1,
bias=False
)
net.weight.data = torch.tensor([[-5.0, 10.0]])
# step2를 위한 사전준비
loss_fn = torch.nn.MSELoss()- 에폭별분해
(미분전) – step1~2 완료
yhat = net(X)
loss = loss_fn(yhat,y)print(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-5., 10.]])
미분값 = None(미분후, 업데이트 진행전) – step3 완료
loss.backward()print(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-5., 10.]])
미분값 = tensor([[-13.4225, 11.8892]])(업데이트 진행후) – step4 의 첫째줄 완료
net.weight.data = net.weight.data - 0.1 * net.weight.gradprint(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-3.6578, 8.8111]])
미분값 = tensor([[-13.4225, 11.8892]])(업데이트 완료 후 초기화까지 끝냄) – step4 의 두번째줄 완료
net.weight.grad = Noneprint(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-3.6578, 8.8111]])
미분값 = None새로운코드의 에폭별분해
- 준비과정 – 옵티마이저라는 오브젝트를 셋팅한다!
# step1을 위한 사전준비
net = torch.nn.Linear(
in_features=2,
out_features=1,
bias=False
)
net.weight.data = torch.tensor([[-5.0, 10.0]])
# step2를 위한 사전준비
loss_fn = torch.nn.MSELoss()
# step3을 위한 사전준비
optimizr = torch.optim.SGD(params=net.parameters(),lr=0.1)- 에폭별분해
(미분전) – step1~2 완료
yhat = net(X)
loss = loss_fn(yhat,y)print(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-5., 10.]])
미분값 = None(미분후, 업데이트 진행전) – step3 완료
loss.backward()print(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-5., 10.]])
미분값 = tensor([[-13.4225, 11.8892]])(업데이트 진행후) – step4 의 첫째줄 완료
#net.weight.data = net.weight.data - 0.1 * net.weight.grad
optimizr.step()print(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-3.6578, 8.8111]])
미분값 = tensor([[-13.4225, 11.8892]])(업데이트 완료 후 초기화까지 끝냄) – step4 의 두번째줄 완료
#net.weight.grad = None
optimizr.zero_grad()print(f'파라메터 = {net.weight.data}')
print(f'미분값 = {net.weight.grad}')파라메터 = tensor([[-3.6578, 8.8111]])
미분값 = None최종코드
- 학습
# step1을 위한 사전준비
net = torch.nn.Linear(
in_features=2,
out_features=1,
bias=False
)
net.weight.data = torch.tensor([[-5.0, 10.0]])
# step2를 위한 사전준비
loss_fn = torch.nn.MSELoss()
# step4를 위한 사전준비
optimizr = torch.optim.SGD(net.parameters(),lr=0.1)
for epoc in range(30):
# step1: yhat
yhat = net(X)
# step2: loss
loss = loss_fn(yhat,y)
# step3: 미분
loss.backward()
# step4: update
optimizr.step()
optimizr.zero_grad()- 결과확인
plt.plot(x,y,'o')
plt.plot(x,yhat.data,'--')
plt.title(f'net.weight={net.weight.data.reshape(-1)}');